基于SMO滑模观测器的异步电机无传感器矢量控制研究：Matlab仿真模型分析

基于SMO滑模观测器的异步电机无传感器矢量控制，matlab，仿真模型。

无感矢量控制在工业界被玩得越来越溜，最近在实验室调了套基于滑模观测器（SMO）的方案。这玩意儿最大的爽点就是不需要速度传感器，靠算法硬怼出转子位置和转速。咱们今天直接上干货，看看Matlab里怎么搭这个坑位。

先甩个滑模面的设计公式镇楼：

function s = sliding_surface(i_alpha_hat, i_alpha, i_beta_hat, i_beta)
    s = [i_alpha_hat - i_alpha; i_beta_hat - i_beta];
end

这坨代码实现了电流误差的滑模面，注意这里用了α-β坐标系下的电流分量。当观测电流和实际电流的差值被逼到滑模面附近时，系统就进入抖振模式——这时候别慌，抖才是正常的。

观测器的核心在于这个非线性反馈环节：

K = 50; % 滑模增益
if s_norm > 0
    v_alpha = K * sign(s(1));
    v_beta = K * sign(s(2));
else
    v_alpha = K * s(1)/epsilon; % 边界层处理
    v_beta = K * s(2)/epsilon;
end

这里有个骚操作：当误差范数超过阈值时用符号函数暴力输出，低于阈值时改用线性处理。实测这个边界层处理能让波形平滑不少，别问我是怎么知道的，示波器前的黑眼圈不会说谎。

转子磁链估计这块得搞个锁相环：

psi_r_alpha = integral(v_alpha - R_s*i_alpha + sigma*L_s*di_alpha);
psi_r_beta = integral(v_beta - R_s*i_beta + sigma*L_s*di_beta);
theta_hat = atan2(psi_r_beta, psi_r_alpha);

积分环节容易漂移，记得加个复位机制。有一次忘加复位，转子角度估计值跑着跑着开始跳机械舞，差点把电机给送走。

转速估算更刺激：

omega_hat = (psi_r_alpha.*d_psi_r_beta - psi_r_beta.*d_psi_r_alpha)...
           ./ (psi_r_alpha.^2 + psi_r_beta.^2);

这本质上是对磁链求导的操作，但直接微分会引入噪声。后来改成自适应律计算，代码没截全，反正最后加了个低通滤波器才稳住。

在Simulink里搭模型时，注意这几个坑点：

1. 电机参数里的转子时间常数必须准，误差超过20%估计值就开始蹦迪
2. S函数里别用固定步长，否则符号函数切换时容易数值爆炸
3. 速度环PI参数要比平时调大30%左右，毕竟观测器有滞后

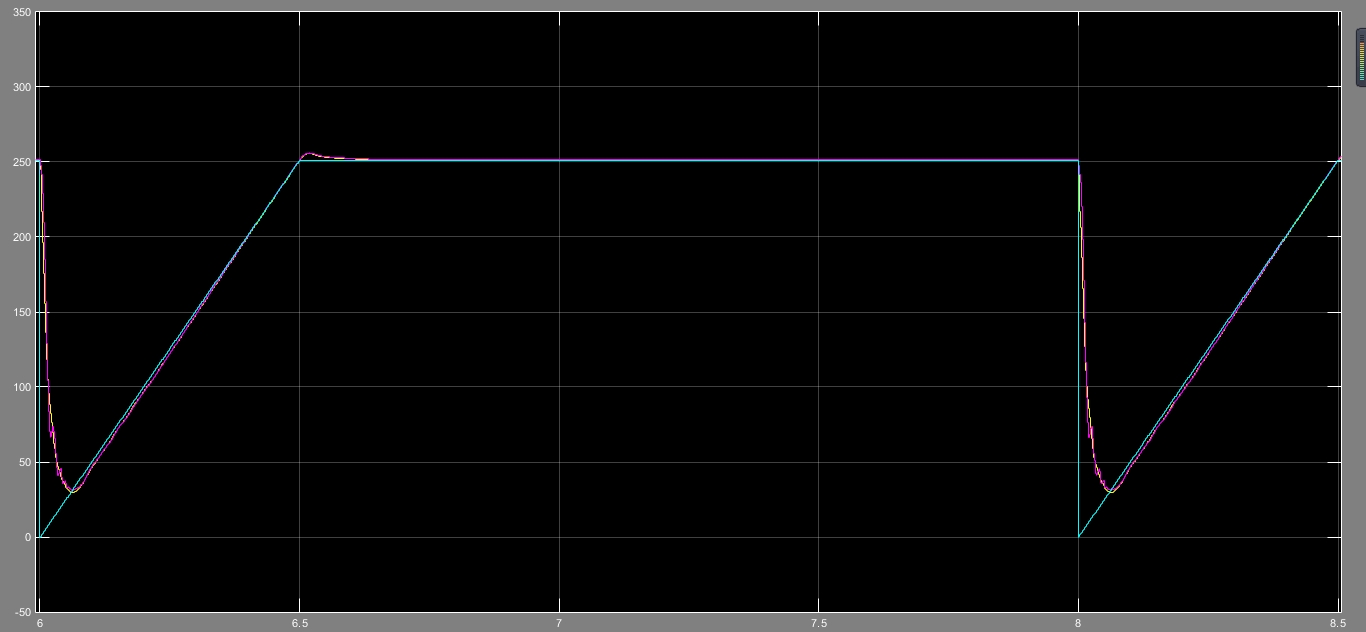
跑出来的波形挺有意思：给定转速从0飙到1500rpm时，估计转速会有个200ms左右的延迟，但稳态误差能压在0.5%以内。突然加个负载转矩，转速估计会出现个尖峰，不过滑模观测器比龙伯格观测器恢复得快得多。

最后安利个调试技巧：把滑模增益K做成在线可调参数，运行时边改边看波形。当K值增加到某个临界点时，电机声音会突然变安静——恭喜你找到最佳工作点了！

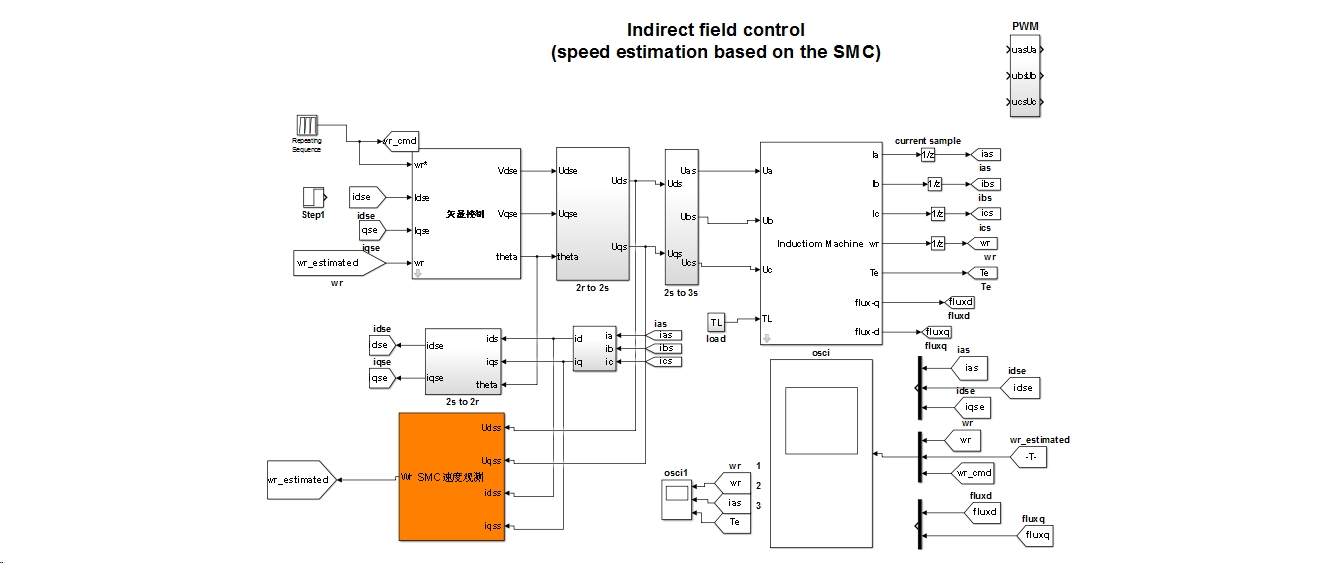
（仿真模型里用了PMSM_Testbench模块，坐标变换那块记得检查Clarke变换的系数是2/3还是sqrt(2/3)，这个坑至少浪费了我两包烟的时间）