永磁电机矢量控制 | 传感器控制

原创已于 2025-03-08 00:17:15 修改 · 2k 阅读

15 ·

CC 4.0 BY-SA版权

文章标签：

#永磁电机矢量控制

于 2024-11-29 02:31:38 首次发布

mechatronics 专栏收录该内容

2 篇文章

订阅专栏

注：本文为 csdn 功夫博主 沉沙丶 的《永磁同步电机矢量控制》系列合集。
略作重排，如有内容显示异常，请看原文。

永磁同步电机矢量控制基础补充（一）——如何绘制电机输出的磁链

沉沙丶于 2020-03-04 16:44:53 发布

在仿真过程中，电机的磁链输出是一个重要的参考指标，在电机运转过程中，磁链的变化过程能够更直观的表现电机的运行状态。因此，如果能够在matlab里面绘画出磁链的运行轨迹，对于电机模型的运行状态就有了更加直观的观察方式。

1、磁链轨迹自身的意义

SVPWM调制方式的根本目标就在于控制磁链轨迹更加接近圆形，从而控制电机运行更加平稳。因为磁链轨迹和空间电压矢量是垂直关系，其实现的方式即控制空间电压矢量间接控制磁链轨迹。由电机的运动方程可知，其在磁场中的受力基于通电导体在磁场中受到力的作用的原理，所以磁场的品质也就决定了电机输出力矩的品质，因此优化电机的磁链轨迹就会提升电机的输出特性，如果能够在搭建仿真的过程中，可以观察到磁链轨迹的运行情况，将有助于我们对整个系统的运行进行更加深入的理解。其示例如下：

2、如何绘制磁链轨迹

磁链轨迹的观察一般将alpha和beta轴的磁链画在同一个坐标系中，以alpha轴作为横轴，以beta轴作为纵轴，在得到以上两个量之后，通过matlab内的plot函数进行绘制。plot函数的使用，请参照我的博文对于matlab工具函数搜集这篇。

关于plot函数的一切（史上最全总结）-优快云博客

https://blog.youkuaiyun.com/T_just_for_tomorrow/article/details/104431429

2.1 得到目标数据

在电机运转过程中，会输出iaibic等一些物理量，那将如何得到alpha和beta坐标系（两相静止坐标系）下的磁链强度呢？异步电机模型会输出dq轴磁链强度，经过变换就可以得到alpha和beta轴磁场强度。而永磁同步电机在simulink内的模型输出并没有磁链强度这一项，只有iaibic电流量。在部分论文中也有通过alpha和beta的电流观察的，我们先观察一下电流的情况，然后再对磁链进行计算分析。

2.2 将示波器中的波形数据导入工作区

下一个问题就是将波形的数据导入到matlab工作区，供plot函数使用，其方法如下左图所示，将其示波器的logging选项卡设置为如下形式，可以看到此时我的示波器命名为iaib。其中保存的数据格式为Structure格式，要将 Log data to workspace选项打上勾。再运行仿真后就会在仿真工作区得到一组如下右图所示的数据，此时的数据就在signal里面，在示波器中signal是纵轴变量的大小，也即是我们需要的alpha和beta的电流大小。

2.3 数据提取与画图

此时的数据还是结构性的，需要经过一下算法进行数据的提取，将其赋值在两个新的数组中，供plot函数使用。我的这个命名方式下的数据提取代码如下，画图的结果如最后的图片所示。

alpha=iaib.signals(1).values;
beta=iaib.signals(2).values;
plot(alpha.beta);

左图为alpha和beta电流在时间轴下的波形，右图为其绘制的波形。右图圆圈外为启动阶段，大的的圆圈为电流0.5s之后带载阶段，圆心部分的小圆为0.05-0.5s部分恒速运行且不带载阶段。可以看到在稳定运行阶段电流圆轨迹是相当标准的，此时的系统动态新能确实也如图中显示，转矩输出波形较微小，转速稳定。

永磁同步电机矢量控制基础补充（二）——Matlab自带坐标系和书本自然坐标系之间的关系

沉沙丶于 2020-03-11 15:24:38 发布

为什么在搭建仿真过程中，按照书本给出的变换矩阵无法实现正常变换？ 这篇文章就细致的讲一下原因。

在刚开始使用matlab对电机进行建模的过程中，比较容易忽略一个问题。Matlab自身使用的坐标系和书本所介绍的自然坐标系之间并不相同，实际上两者之间相差90电角度。

Matlab 自身使用的坐标系如下左图图所示，而书本介绍的自然坐标系如右图所示

ABC三相之间是完全的相同的，但是 alpha、beta 坐标系之间相差 90°，d、q 坐标系之间相差 90°，这在将导致在建模的过程中，变换矩阵的完全不相同，从而导致变换矩阵错误。

在 Matlab2014 版本之后，电机模型中就多出了一项选项卡来解决以上问题。

在电机选项的 Advanced 选项卡下，rotor flux position when theta = 0，此下拉条下选择跟随A相坐标轴（Aligned with phase A axis( original Park)），也即自然坐标系。选择此选项卡后，即可按照书本介绍的变换矩阵进行变换。

永磁同步电机矢量控制基础补充（三）——如何理解调制度m

沉沙丶于 2020-03-24 11:39:21 发布

在重新进行基础复习时，发现对于调制度的理解只是基于一个公式，只理解到 m 是一个比值，它具体代表什么物理含义？在控制系统运行过程中 m 又与那些物理量有关呢？调制度 m 会跟随什么变化呢？

我们首先看一下SVPWM中调制度的由来。（图片出自袁雷书籍第二章）

再看一篇论文中对于调制度的定义。（来源于知乎https://www.zhihu.com/question/20904325）

可以从上述公式看出，对于调制度的理解可以从这几个方面思考，第一个从公式的角度理解，调制度是计算基本矢量作用时间过程中的比例系数，第二个从SVPWM脉冲生成的角度理解，调制度是调制波峰值和载波峰值的比值（载波比是另外的概念）。

如果要从物理上去理解，应从数学模型上入手。在推导公式过程中，首先Um是相电压的幅值，相电压的幅值决定输出的大小，输出可以理解为更大的转矩输出；Udc是直流母线电压，与逆变器一起决定系统的最大输出能力。已知Udc是一个定值，则调制比的大小跟随相电压幅值的变化，也可以说调节调制比的大小，就是调节输出相电压幅值的大小，调节系统的输出力矩的大小。

小结：

不论是SPWM还是SVPWM，调制度的定义都是相电压幅值Um和母线电压Udc的比值，这个比值越大，其逆变器输出的基波电压幅值也就越大，也代表着系统的输出功率越大，输出力矩越强。电机系统最重要的输出量就是输出转矩，调制度的改变代表着系统输出力矩的改变，从而控制着整个系统的运行。

永磁同步电机矢量控制基础补充（四）——如何设定电流环PI调节器和转速环PI调节器的限幅值

沉沙丶已于 2024-08-16 14:09:47 修改

如何设定电流环和转速环的限幅值，在此具体阐述一下 PI 调节器限幅值设定的参考因素。

1 电流环PI调节器限幅值

在整个系统中，电流内环PI调节器的输出是Ud和Uq的给定值，经过IPark变换转换到两相静止坐标系 Ualpha 和 Ubeta 的给定值。结合前面对于SVPWM的基础，SVPWM的发波原理为：根据两相静止坐标系下的参考电压矢量的相位和幅值，组合基本电压矢量合成参考电压矢量。两相静止坐标系 Ualpha 和 Ubeta 的给定值经过SVPWM模块，生成PWM脉冲，从而使得逆变器输出所需电压矢量（如下图所示）。

因此，电流环调节器的输出限幅值是根据调制方式设定的，SVPWM方式的调制度最大值为1，其表达式如下图所示，因此电流调节器最大输出电压为Udc/1.732。

$\displaystyle M=\frac{\sqrt{3}\mathop{U}_{m}}{\mathop{U}_{dc}}$

有同学提出：为了维持 $i d = 0$ 控制，d 轴必然要有电压输出，而相应的，一旦d轴存在着维持 $i d = 0$ 的分压，q 轴电压就不可能到 $\frac{U}{\sqrt{3}}$ ，因为 $\sqrt{u_q^2 + u_d^2} \leq \frac{U}{\sqrt{3}}$ 。

目前还未明确具体这样考虑带来影响，有想出具体的限幅值原理请留言，感谢！

2 转速环PI调节器限幅值

与电流环相同方式去理解转速环，是一个比较有效的办法。转速环PI调节器的输出是q轴电流 iq 的给定值，而 iq 是控制电机转矩输出的关键物理量。为了纯粹只是讲解限幅值设定，假定此时的控制方式为 $i d = 0$ 控制，根据下图所示的电机运动方程公式可知，此时的转矩完全由 iq 决定。

iq 控制电机的转矩输出，在转速环控制 iq 给定这个基础上，必须要考虑的因素就是电机本身的限制：额定转矩。iq 不能无限增大的原因也是因为电机不可能输出无限大的转矩**。所以根据最大输出转矩计算出来的最大 iq 给定即为转速环PI调节器的限幅值**。

小结：

1、电流环PI调节器限幅值根据调制方式的限制设定，SVPWM调制度最大为1，即限幅值为 Udc/1.732

2、转速环PI调节器限幅值根据最大输出转矩的限制设定，根据额定转矩计算iq限幅值。

永磁同步电机矢量控制基础补充（五）——什么是低通滤波器？

沉沙丶已于 2024-08-16 14:09:26 修改

最近在做滑模控制的时候，遇到了一个不太理解的概念——低通滤波器。从其名字上理解为通低频、阻高频的滤波器。但如何根据实际情况来设置滤波器呢？这就是问题的关键。

1 什么是低通滤波器

低通滤波器是容许低于截止频率的信号通过，但高于截止频率的信号不能通过的电子滤波装置。换句话说，它将信号的频谱分离为将要通过的频率分量和将被阻塞的频率分量，且这部分被阻塞的频率分量是高频分量。而这个通过和阻塞的临界值被称为截止频率。

2 什么是截止频率

从频域响应的角度讲，当保持输入信号的幅度不变，改变频率使输出信号降至最大值的0.707倍，即用频响特性来表述即为-3dB点处即为截止频率，它是用来说明频率特性指标的一个特殊频率。（如何求截至频率在此不再赘述，请查阅自动控制原理数据频率特性章节内容）

可以通过在matlab内测试，来直观的观察截至频率，下图低通滤波器的截止频率为10。

（10/（s+10）的形式时10就是截至频率）

如果通入正弦波，分别为sin(t) 、sin(5t)和sin(10t)，前后正弦函数的频率为分别1/2pi =0.16Hz、5/2pi=0.8Hz 、 5/pi=1.6Hz，滤波结果如下图所示:

观察波形发现（红色为输入，蓝色为滤波后的输出）。从第三章图可以看出，在输入信号为sin(10t)时，经过低通滤波器输出的信号幅值为0.707，它相对于输入信号相位滞后了45°。

在此通过实验现象验证了截止频率的定义——当保持输入信号的幅度不变，改变频率使输出信号降至最大值的0.707倍，此时的频率为截止频率。

3 截止频率的单位是 Hz 还是 rad/s？

这里需要有个问题注意一下：

对于低通滤波器 $\frac{10}{s+10}$ ，其截止频率为 10，但这个单位是什么呢？是赫兹 Hz 还是 rad/s 呢？

通过下面波形探究一下，其中蓝色为 $y=\sin(t)$ ，红色为 $y=\sin(2t)$ ，绿色为 $y=\sin(2\pi t)$ 。

对于 $y=\sin(t)$ 和 $y=\sin(2\pi t)$ 单独讨论：

$y=\sin(t)$ 用了 6.28s 走完一个周期，频率为 0.16 Hz（1 rad/s）；
$y=\sin(2\pi t)$ 用 1s 走完一个周期，频率为 1 Hz（2π rad/s）；

同理可以推断， $y=\sin(10t)$ 用 0.628s 走完一个周期，频率为 1.6 Hz（10 rad/s）。

对于低通滤波器 $\frac{10}{s+10}$ ，其截止频率为 10。

**因此此处可以得到结论，根据低通滤波器计算出来的截止频率的单位为 rad/s **。

小结：

1、截止频率：当保持输入信号的幅度不变，改变频率使输出信号降至最大值的0.707倍时，此时频率为截止频率，相位之后45°。

2、根据低通滤波器计算出来的截止频率的单位为 rad/s ， $\frac{10}{s+10}$ 的截止频率为 10 rad/s。

文章中验证的模型已经贴粗来啦，另外后面对于单位的讨论其画图程序为：

t=0:0.001:6.28;
y=sin(t);
figure(1);
plot(t,y,'b');
hold on
y1 = sin(2*t);
plot(t,y1,'r');
hold on
y2 = sin(2*pi*t);
plot(t,y2,'g');

永磁同步电机矢量控制基础补充（六）——如何在simulink初始化电机参数？

沉沙丶于 2020-05-06 11:41:31 发布

最近有很多同学问，在模型里面为什么有Ld、Lq、Ts等参数，这些参数如何设置。这些参数在simulink里面是可以宏定义的，也就是可以初始化。

1、初始化参数的优点

这么做有以下几个有点：

便于修改参数。在模型参数需要修改时，不用一个参数一个参数的修改且避免漏改的情况，只用更改初始化参数。
提高模型的可读性。在读取程序的原理时，可以知道当前物理量定义，而不是一堆数字，还需要大脑里去将数字和物理量匹配。

2 如何设置参数？

操作步骤如下：

步骤一：进入Model Properties 界面（file----->Model Properties）

步骤二：在Model Properties 界面进入 Callbacks选项卡内的 InitFcn*界面。在这个地方定义的量，可以在模型内直接用代号的形式书写，如下左图对解耦的公式搭建，直接用符号就可以，非常方便。

永磁同步电机矢量控制基础补充（七）-（深度剖析结构）模块化解释矢量控制

沉沙丶于 2020-05-12 18:40:17 发布

这段时间有比较多同学问到我一个相同的问题，这矢量控制一块又一块的，干啥非要整成这个样子，矢量控制的整体结构为什么是这样的？ 哈哈哈哈，当时可把我给问住了，这可真是个令我头发飞舞起来且秃头的问题。可能对于刚刚进入矢量控制的我们来说哈，这一下有了这么多书有了这么多资料，到底又该从何下手呢？这样的提问不禁让我觉得框架结构的理解其实是一个很重要的问题。在开始系统学习之前，如果能够对整个系统有一个大体的概念；在不知道具体细致原理之前，如果能够初步了解各个模块的作用，以及各个模块协同工作的联系，那么在深入细致的学习时就会感到更加踏实，就像玩游戏的时候，知道自己到底在攻破哪个关卡，这种学习的成就感就油然而生。因此我希望在此，通过我自己的一些个人总结，把整个原理框架给大家初步的阐述一下，有不对地方还希望大家指正。（此篇文章主要从各模块作用的角度上阐述矢量控制，如何通过这一个一个积木搭建成为一个系统）

总体矢量控制结构框架

矢量控制原理框图如下图所示，我将其分为主要的7个小的模块进行阐述，模块代号在下图中已标注出来。

1 Clark变换模块（3s/2s变换）

下图为永磁同步电机在三相坐标系下的磁链方程，可以从中看出三相永磁同步电机是一个复杂的系统，具有多变量、强耦合以及非线性的特性，因此在三相静止坐标系下对永磁同步电机进行直接控制是比较困难的。通过坐标变换与解耦运算的方法，使得各个物理量从静止坐标系转换到同步坐标系。将定子电流分解为互相独立的历次电流和转矩电流，且均为直流量。这样就能够分别对励磁电流和转矩电流进行实时控制，以达到直流电机的控制性能。（直流电机的性能优越的原因是独立控制励磁电流和转矩电流，这两者能够独立控制，就可以控制何时施加转矩，就可以按照需求随意控制电机是否转动转多快的问题）

Clark 变换的作用就是将三相坐标系的量转换到两相静止坐标系。这里我们不禁提出一个问题，为什么要换到两相静止坐标系呀?其实有个最简单的道理在里面，直角坐标系的纵轴和横轴之间相互垂直，各自发展趋势对彼此相互不影响，其数学模型中的变量更容易实现独立控制，这是三相坐标系不具备的优点。

2 Park变换模块（2s/2r变换）

在经过Clark变换后，电机的数学模型已经坐落在两相静止坐标系了，但由于PMSM也分为转子和定子，两者之间的不同步，无法通过控制一个电流就能实现对磁场或者转矩的控制，因为控制逆变器定子侧的电流，对转子的控制还受到位置因素的影响，相同电流不同位置控制效果不同，所以还需要解耦。如果能够实现定子和转子同步旋转呢，就可以使得两者处于相对静止状态（书上描述为旋转磁动势的大小和转速和固定的交流绕组产生的旋转磁动势相同），此时就跟直流电机没有任何区别了，一个电流控制励磁，一个电流控制转矩。

所以Park变换的作用就在于剔除位置信息对控制的影响，使得同步电机在两相坐标系下，等效为直流电机，但此时又在旋转所以称为两相旋转坐标系。

注：变换这部分需要细究的同学，请查阅陈伯时运动控制系统的6.6节坐标变换内容，讲得极其详细。

344 PI调节器模块

电流调节器和转速调节器在模块搭建上是分开的，但其实两者在功能上是一致的，所以在这里将两者放在一起叙述。

PI调节器在所有领域，它根据给定值与实际输出值构成度控制偏差，将偏差的比例和积分通过线性组合构成控制量，对被控对象进行控制。PI调节可以按照比例反应系统的偏差，系问统一旦出现了偏差，比例调节立即产生调节作用用以减少偏差。

P：比例， I：积分。PI调节叫作：比例、积分调节。它的原理是通过比例积分（指对输百入、输出偏差的作用）调节器（作用），控制输出信号符合设定值。

比例调节作用：按比例反应系统的偏差，系统一旦出现了偏差，比例调节立即产生调节作用用以减少偏差。比例作用大，可以加快调节，减少误差，但是过大的比度例，使系统的稳定性下降，甚至造成系统的不稳定。

积分调节作用：使系统消除稳态误差，提高无误差度。因为有误差，积分调节就进行，直至无差，积分调节停止，积分调节输出一常值。更详细的介绍还得上小破站：https://www.bilibili.com/video/av42262043（视频不见了）

回到电机控制系统，无论是电流 PI 调节器还是转速 PI 调节器，都是将给定值和反馈值的误差转化为下一个环节的给定值。

例如，在转速 PI 调节器中，回到文章的第一张图，将给定转速和反馈转速的误差转化为 $i_q$ 的 PI 调节器的给定值 $i_{qref}$ ，以实现对转矩的控制。从这里可以理解：

当给定转速大于反馈转速时，输出转矩为正，需要电机加速；
而当给定转速小于反馈转速时，输出转矩为负，需要电机减速。

回到电机控制系统，无论是电流PI调节器还是转速PI调节器，都是给定值和反馈值的误差转化为下一个环节的给定值。例如转速PI调节器，回到文章的第一张图，将给定转速和反馈转速的误差转化为 iq 的PI调节器的给定值 iqref，实现对转矩的控制，从这里就可以理解为什么给定转速大于反馈转速的时候，输出转矩为正，需要电机加速；而给定转速小于反馈转速时，输出转矩为负，需要电机减速。

4 Ipark变换模块

此模块作用是将两相旋转坐标系下的Ud和Uq转化为两相静止坐标系下的Ualpha和Ubeta，这里估计就有铁汁们就要问了，你不都花了老大劲变过去了，咋滴又变回来是个啥情况啊。

其实原因在于哈，我们最终控制的三相逆变器他是铁骨铮铮的三相静止坐标系模型啊，三相全控桥六个开关三个独立相可不能被我等小辈在此耍花招变来变去，大家不妨记住一个常理电力电子的都是铁汉！电机控制的都是花里胡哨的（开个玩笑）。所以在Ud和Uq给定后，我们得把他变回去，通过SVPWM模块转化为对应的脉冲序列，对逆变器进行相应的控制。

5 SVPWM模块

这部分就是空间矢量控制技术，其原理是从电机的角度出发使得电机处于幅值固定，可跟随电机转子旋转的旋转磁场，即磁通正弦。它以交流电机所用的理想磁通圆为参照，把三相对称的正弦波电压产生的理想磁场作为参照，对逆变器的开关进行有序的组合，使得产生的磁通能够逼近基准圆磁通，最终可以得到逆变器的不同开关状态的组合，而这些组合的控制是通过PWM的形式来控制的。

此部分的作用在整个控制框架内，是对Ipark模块变换出来的给定电压Ualpha和Ubeta进行脉冲实现，也就是通过SVPWM产生于相应的脉冲使得逆变器输出的电压于Ualpha和Ubeta一致。

此部分其实具有相当多的内容，具体请参照此链接内的文件

下载链接：https://pan.baidu.com/s/1FAfFQVdmjFI0xYJPSmAOXA
提取码：4jxg

此链接下更是讲得极尽详细生动活泼，给大家推荐以下https://www.cnblogs.com/ly0019/p/9053875.html

小结：

从上述内容可以总结出一个信号的流程，此流程从电机出发，经过电机三相静止坐标系下电流iaibic 、两相静止坐标系电流ialpha 和 ibeta，两相旋转坐标系电流 id 和 iq，两相旋转坐标系给定电压 Ud 和 Uq ，两相静止坐标系给定电压 Ualpha 和 Ubeta，6路PWM脉冲信号。我自己画了一个信号流图。铁汁可以两个图结合起来看，就知道具体整个系统是怎么运行的了。

永磁同步电机矢量控制基础补充（八）——Matlab/Simulink打开仿真出现的问题汇总

沉沙丶于 2020-05-18 16:25:30 发布

问题：低版本软件打开高版本仿真时

解决办法：（仿真版本在matlab界面左下角，如右图所示）

方法一：更新软件版本，这个方法较为费时费力，毕竟matlab好多个G

方法二：找有高版本软件的同学输出与你软件匹配的版本。具体操作如下图所示，然后选择什么版本就看自己的啦。

永磁同步电机矢量控制基础补充（九）——Simulink软件的入门学习

沉沙丶已于 2024-08-16 14:09:09 修改

基础部分：

Simulink入门视频教程及其参考书籍+基于Simulink代码生成技术视频教程及其参考书籍

此部分为Simulink基础入门视频教程，Simulink软件本身是具有一定难度的，但是对于电机控制系统而言，其仿真效果又是最为优越，仿真结果与实际运行情况最为贴近的一款软件，是电气领域和电机控制领域必须要掌握的工具之一。本部分视频教程也是笔者入门时学习的教程，其视频讲解细致，对于软件的操作会细致的演示，对于无基础的同学而言较为适合。打好软件的基础，是对后续模型理解的基础，也是实现后面第三部分矢量控制，到第十部分三闭环等所有控制理论部分的基础，望仔细观看。

下载链接：Simulink入门视频教程及其参考书籍资料

https://pan.baidu.com/s/16YX9Z5M5XFcHyYEaYEtcng

提取码：c09m

另外一部分为基于Simulink代码生成技术的视频教程和参考书籍，此部分主要对需要实际应用的同学起作用。毕竟纯粹靠手动去编程效率低且容易出错，对于原理必须要极其深刻的理解才能手写正确的程序。代码生成技术是在模型实现的基础上，能够直接生成控制器代码，写入到芯片内，只要接口配置合适，内部逻辑与计算都是严格按照仿真进行。这也是现在嵌入式的一个趋势，基于代码生成的工序，一般按照搭建仿真 ==> 仿真出结果 ==> 生成代码 ==> 下载入芯片调试电机进行，其中生成代码只需要matlab自动进行，时间为一分钟左右，但认为编写代码可能需要好几个月时间。对于需要实验和提高调试效率的同学，这部分资料能够较好提高自己的技能水平，这也是找工作时解决只会搞理论的担忧。

下载链接：Simulink代码生成技术视频教程与参考书籍

https://pan.baidu.com/s/13NHUvFMLW7Ggw8VAi7D1Dg

提取码：popi

永磁同步电机矢量控制基础补充（十）——调制模式和控制方式之间的区别？

沉沙丶于 2020-06-12 16:31:41 发布

近段时间经常有同学和我讨论**：矢量控制是什么控制方式？双闭环控制策略就叫做矢量控制吗？**

其实刚开始学习难免会对矢量控制的概念有所模糊，具体是对于调制模式和控制方式之间的区别不太清楚。在此具体讲述一下如何对调制模式和控制方式两个名词的概念进行区分，各式各样的调制方式和控制方式又是基于什么得来的？

1 什么是调制模式？

对于电气领域，调制模式主要应用在逆变器上，以三相逆变器（如下左图所示）为例，控制系统需要特定的6路脉冲序列（PWM）驱动逆变器中的6个开关管，从而使得直流电被转化为我们需要的交流电，驱动电机旋转。

调制模式就是如何生成这个所需脉冲序列（PWM）的方法。在我的理解中，调制模式就是基于如何驱动逆变器而产生的概念，它主要强调了依据指令电压生成脉冲序列（PWM）的过程，例如我们熟知的SVPWM空间矢量调制技术，其目标就是为了得到电动机定子理想磁链圆（如上右图所示），并根据这个目标来生成相应的脉冲序列（PWM），SVPWM的名称也是来源于它的调制目标。再举个例子，经典的SPWM调制技术，其目标是为了使得逆变器输出电压尽量接近正弦波，并依据此目标生成脉冲序列，因此被成为Sine PWM。

所以根据以上两个例子，对于调制模式的定义我们可以得到两个关键点

调制模式是如何生成脉冲序列（PWM）的方法
调制模式的命名是根据其调制目标来确定的

2 什么是控制方式？

我们经常可以听到基于id=0的控制、最大转矩电流比（MTPA）控制、弱磁控制、三闭环位置控制等等这些名词，其实仔细揣摩不难发现，这些名词都包含了对系统的某个性能目标的控制，比如三闭环位置控制，其控制目标就是位置，位置控制实现的方法就是三闭环。

那么具体如果概括的说控制方式是什么呢？就我个人的理解而言，控制方式是从整个电机控制系统的控制目标和控制过程出发，对整个控制系统的控制目标和实现过程进行阐述。

如果说调制模式是强调如何依据指令电压生成脉冲序列（PWM）的过程，那么控制方式强调的就是如何根据电机状态（各种实时电流电压大小）得到指令电压的过程。例如我们熟知的双闭环速度控制系统，其目标就是为了控制电机的转速按照给定转速运行，依据电机实时转速状态得到指令电压的大小，从而控制电机到达我的给定转速。再举个例子三闭环位置控制系统（如上图所示），其目标是为了控制的电机转到我指定的位置，依据电机的实时位置、通过三个闭环PI调节器得到指令电压的大小，从而控制电机转到我想要他转到的地方。

同样可以根据以上两个例子，对于控制方式的定义我们可以得到两个关键点：

控制方式强调的是如何得到指令电压的方法
控制方式的命名是根据其控制目标和控制过程来确定的

3 两者的区别和联系

两者的区别就在于**：控制方式强调如何根据电机状态和控制方式生成指令电压，而调制模式强调如何根据指令电压生成脉冲序列**。两者的目标不同，实现的方式也不同。如果说从输入输出的角度考虑，两者的不同将更加明显，控制方式的输入是电机状态量，输出是指令电压量；而调制模式的输入是指令电压量，输出是驱动逆变器运行的脉冲序列（PWM）。

可以从以上的输入输出的分析得到两者的联系，调制模式是实现控制方式的基础，而控制方式则是调制模式指令电压的来源，只有优良的控制方式和较好的调制模式，才能共同实现性能优越的系统控制。

因此文章开头的问题就可以得到解决了，如下框图所示，其中绿色区域为控制方式部分，而黄色区域为调制模式部分。那么所谓的矢量控制系统如果完全阐述出来就是：基于SVPWM控制矢量调制策略的id=0双闭环控制系统，简称为基于id=0的双闭环矢量控制系统，矢量两个字代称空间矢量调制技术SVPWM。

永磁同步电机无速度传感器控制（一）——滑模观测器（一）【位置估计原理】

沉沙丶已于 2022-09-03 00:10:18 修改

无速度传感器控制就从滑模开始吧，基于反正切函数的转子位置估计应该是无速度传感器里面稍微简单的一类啦，就拿这个入手啦~滑模反正切分为多个文章进行解释，观测器数学和物理原理、观测器效果和波形分析。

1、滑模观测器

滑模控制是一种特殊的非线性控制系统，它与常规控制的根本区别在于控制的不连续性，即一种使系统‘结构’随时变化的开关特性。这种方法实现的关键在于滑模面函数的选取和滑模增益的选择，滑模面函数决定了观测函数的准确性，滑模增益决定了估算的收敛速度。因此一个好的滑模观测器，既要保证滑模面函数的准确性，还需要保证滑模增益大小适合。滑模增益本身并不是越大越好，而是需要在既满足收敛速度，又能使得系统稳定运行（增益过大会导致抖振）。

由于滑模控制对系统的模型精度要求不高，对参数变化和外部干扰不敏感，所以它是一种鲁棒性很强的控制方法，因此在实际应用中，使用范围较广，是一种较为值得学习的控制方法。

对于永磁同步电机PMSM而言，*滑模控制是基于给定电流和反馈电流间的误差来设计滑模观测器的，并由该误差来重构电机的反电动势，并估算转子速度和转子位置信息*。具体的，就开始讲述如何对PMSM设计滑模观测器了。（上述介绍出自袁雷书籍5.1章节，稍微加了一点自己的理解）

2、PMSM的滑模观测器位置估计的基本原理

本文介绍的滑模观测器是基于两相静止 α 和 β 坐标系下的数学模型进行设计的，在两相静止坐标系中，PMSM电机的电压方程为：

             ![img](https://i-blog.csdnimg.cn/blog_migrate/9d3ae27949ad51c11119c6ad3ec68e6f.png =700x)

式中，Ld 和 Lq 分别未dq轴电感，p为微分算子（p= d/dt），we 电角速度，R为定子电子，Ea 被 Eβ 为扩展反电动势。为了简便后面的公式符号简略介绍。

其中扩展反电动势是一个重要的概念，其表达式为：

         ![img](https://i-blog.csdnimg.cn/blog_migrate/c47e750b64353c7d3eb2d36fda7384bf.png =700x)

从上面关系是可以得到两个重要信息，第一个：Ld = Lq 时（表贴式电机），扩展反电动势与电流无关，只与电角速度、永磁磁链强度和电机转子位置 theta 有关。第二个：可以看到扩展反电动势内包含着 theta 角，也即位置信息，那么如果能够实现对扩展反电动势的计算或者估计，就可以通过对其进行求解得到位置信息。为了更快入门，我们先从简单的表贴式电机的滑模开始进行学习。

以上所阐述的分析可知，扩展反电动势包含转子位置信息，并且 α 和 β 轴的扩展反电动势的反正切函数正好就等于位置角theta。总结可得，滑模观测器实现位置估计的基本原理：通过滑模观测器观测得到扩展 α 和 β 轴的扩展反电动势大小，并求其反正切函数，得到位置信息。

今天先就写到这里，滑模观测器的实现位置估计的原理已解释清楚，具体滑模观测器的设计过程。

永磁同步电机无速度传感器控制（一）——滑模观测器（二）【滑模观测器设计过程】

沉沙丶已于 2022-09-03 00:10:03 修改

1、选择滑模观测器参照的数学模型

对于表贴式三相PMSM而言，扩展反电动势的表达式可以被简化为与仅与电机的转速有关。然后将表贴式PMSM的扩展反电动势表达式写下来，进行分析:

从上式可以看出，只要可以得到扩展反电动势（EMF）的大小，即可通过求取反正切值求取实际位置 theta 值。

对于观测器的设计，一般会选取一个数学模型进行参照。而对于PMSM而言，一般会根据电机的电压模型或者电流模型来设计观测器**。由于电机的负载状态会影响扩展反电动势的大小，而电机在高速重载的情况下，定子电流将会有较大的变化。因此，对于估算扩展反电动势的滑模观测器，按照PMSM的电流模型来设计会更合理**。

因此将PMSM的电压状态方程，改写为电流状态方程的形式，将其作为滑模观测器的参照模型。

2、滑模观测器的设计

为了估算扩展反电动势 Eα 和 Eβ ，对滑模观测器的设计如下方程所示：

观测器在形式上和实际电机的数学模型完全一致。这么设计的原因**：由于实际电机电流模型中包含扩展反电动势的大小，如果我们设计的滑模观测器模型，能够通过实时校正，逐步的逼近实际的电机模型，当观测器模型与实际电机模型完全一致的时候，观测器模型内的扩展反电动势参数即为我需要的实际电机扩展反电动大小**。这个道理就类似于，我无法实际的去测量博物馆玻璃罩中珍藏的文物，那如果我扫描一个镜像出来，去手把手测量这个镜像的长宽高，一样可以得到我们需要的信息。而滑模观测器的设计就是基于这个原理。

3、滑模面的选取

将上述两个数学模型进行做差，可以得到如下定子电流误差方程：

如果能够使得实际 α 轴定子电流和 β 轴定子电流一致，那么滑模观测器的扩展反电动势也和实际电机的扩展反电动势一致。因此可将滑模面设计为：

4、滑模控制律的设计

滑模控制律的设计是基于滑模变结构控制器的。滑模变结构控制器的原理（滑模观测器原理与其相同）如下图所示：

如上图所示，其中A点穿过滑模面，B点由滑模面扩散，C点从其他地方回归至滑模面。只有C点才能使得系统最终趋于稳定，使得系统回归至滑模面。滑模控制律的设计就是要实现C点的功能**：当系统参数在滑模面以上时，使其运动轨迹向下；当系统参数在滑模面以下时，其运动轨迹向上，其运动时刻向着滑模面**。

因此开关函数 sgn() 为滑模观测器的实现提供了坚实基础。当系统参数运行至滑模面以上时，sgn = -1 ，其运动轨迹向下了；当系统参数在滑模面以下时，sgn = 1，其运动轨迹向上了。

*对于扩展反电动势的滑模控制律设计而言，就是使得电流回归滑模面，使得观测器电流和实际电流之间的误差为0，则观测器扩展反电动势等于实际电机扩展反电动势*，因此可将其滑模控制律设计为：

小结：

1、滑模观测器的设计过程可以分为：选择观测器参照数学模型、设计观测器模型、选择滑模面、设计滑模控制律

2、电流对于扩展反电动势影响较大，所以估算扩展反电动势的滑模观测器选择PMSM的电流模型。

3、如果能够使得实际 α 轴定子电流和 β 轴定子电流一致，那么滑模观测器的扩展反电动势也和实际电机的扩展反电动势一致。

4、对于扩展反电动势的滑模控制律设计而言，就是使得电流回归滑模面，使得观测器电流和实际电流之间的误差为0，则观测器扩展反电动势等于实际电机扩展反电动势

永磁同步电机无速度传感器控制（一）——滑模观测器（三）【由扩展反电势得到电机位置和速度信息】

沉沙丶已于 2022-09-03 00:10:35 修改

1、直接求反正切函数的不足之处

上一篇文章，写到了滑模观测器的设计过程，此过程过后可以得到滑模输出的扩展反电动势。按照反正切函数的原理，只需要对扩展反电动势进行求解反正切即可。如下所示：

但是事实上，直接通过滑模观测器输出的扩展反电动势是无法得到准确的实际位置信号的。其原因是：

滑模观测器时刻在滑模面上下抖振，输出的扩展反电动势包含不连续的高频切换信号，直接求取结果抖振严重

因此，为了提取连续的扩展反电动势估计值，通常需要外加一个低通滤波器（低通滤波器的原理我有篇基础补充博客详细说明了，请大家查阅），滤除高频切换信号。如下所示：

2、低通滤波器的相位延迟补偿

但是呢，低通滤波器这个东西是个双刃剑，它的使用也会造成一些没办法避免的问题**：当高频信号被滤除后，扩展反电动估计值的幅值和相位都会发生变化，这个变化造成的幅值减小和相位延迟都会直接影响转子位置估计的准确性**。

这个不准确性当然就是我们不想看到的了。所以，在实际应用过程中，为了解决低通滤波器造成的幅值减小以及相位延迟，需要根据低通滤波器自身的截止频率进行延迟补偿。补偿原理如下所示：

式中 wc 为低通滤波器截至频率，we 为估计转速。式中估计转速同样可以通过估计的扩展反电动势得出。

3、滑模观测器实现原理框图

综合上面所说的全部内容，我们可以总结滑模观测器的实现原理如下框图所示，先通过滑模观测器得到扩展反电动势，然后对扩展反电动势进行滤波处理提出有用的信号，进而对使用的低通滤波器进行相位补偿，最终通过补偿后准确的扩展反电动势信息得到位置角和速度信息。这样一下子下来，我们的无速度控制就完成啦。^_

总结而言，在通过滑模观测器得到估计的扩展反电动势之后，若需要得到实际的电机位置信息还需要以下几个步骤：

设计低通滤波器，对滑模出来的高频切换信号进行滤波处理
对低通滤波器造成的相位延迟进行补偿，
通过反正切函数求取位置 theta ，通过估计转速公式求取转速 we

小结：

以上已经将滑模观测器实现无速度传感器控制讲完啦，也算是完成了一个小课题啦，有兴趣的同学也可以完整的走一遍哒，无论是花多少实践，都会有收货的。

另外，回归原理说说，我们可以发现在经过了滑模观测器得到扩展反电动势之后，其实还需要对信号进行处理才可以得到准确的位置信号。滤波器的使用常常就是这样，它确实能帮我们提出需要的信号，对信号进行优化处理，但是它本身带来的问题其实也不少。从自动控制原理的角度，低通滤波器就是一个传递函数，当它加入到系统中的时候，它实际上是成为了系统通路上的一个环节。这个新增的环节无论如何都会给系统带来影响，所以相应对滤波器的补偿研究也不少，还需要继续往下呀~

永磁同步电机无速度传感器控制（一）——滑模观测器（四）【仿真搭建及其结果分析】

沉沙丶已于 2022-09-03 00:10:51 修改

1、滑模仿真框图

2、仿真结果

波形的简要分析

1、转速响应曲线

下图为滑模无位置控制的转速响应，其中蓝色为估计转速，内部被遮盖的为实际转速，可以从图中看出，估计转速和实际转速基本重合，验证了滑模观测器的有效性。对转速响应曲线种的分析为其动态性能，此时给定转速为800rpm，可以看到在短暂的振荡过后，电机实际转速到达给定转速，此处验证了系统的准确性。在0.05s（箭头处）是电机突加负载，电机在短暂的速度降落之后，迅速回升到给定转速，此处验证了PI调节器的抗扰动性能。

2**、位置跟随曲线**

此处与上述转速波形类似，红色为估计位置，而蓝色为实际位置，可以从图中看到估计位置与实际位置曲线基本重合，滑模观测器的准确性进一步得到验证。且在0.05s施加负载后，位置仍然能够快速跟随，验证了滑模观测器的快速收敛特性。

3**、转矩曲线和三相定子电流曲线**

在启动阶段，可以看到转矩迅速上升至最大值，此时转速调节器饱和，在上升到给定转速后快速下降，验证了系统的快速性。在0.05s施加5N负载后，转矩输出迅速增大为负载大小，此处验证了系统具备较好的抗扰动性能。

资料链接：

链接：https://pan.baidu.com/s/1FIrezc-PAqBylqqVvO0IaA

提取码：8888

永磁同步电机无速度传感器控制（二）——脉振高频注入法（一）【位置估计原理】

沉沙丶已于 2022-11-15 20:22:45 修改

1、高频注入法

前面已经讲过了一种无速度传感器实现方法——滑模观测器法。在开始一个新的位置估计策略之前，我们先聊一聊这个方法本身的特点。从前面对滑模的讲述可知，滑模观测器法是通过构造一个滑模面，然后设计滑模控制律，进而得到扩展反电动势，实现位置信息的观测。但这个过程其实涉及到一个很重要的问题，滑模在零低速情况下能够有效吗？滑模观测器设计的根本目标是得到扩展反电动势，从而得到位置信息。电机在零速情况下没有扩展反电动势，低速情况下反电动势谐波成分含量大，因此滑模等一系列通过反电动势来观测位置信息的方法，在零低速情况下，均无法准确观测出电机的位置信息。

那么如何解决呢？利用高频信号注入法。此方法主要利用电机自身的非理想特性对电机的转速和位置信号进行估计。主要原理是在电机定子侧注入高频电压或者高频电流信号，注入的高频信号在电机内会形成高频磁场。由于电机具有非理想特性，例如转子结构凸极性、转子饱和凸极性等，这种非理想特性会对高频磁场产生调制作用，使得电机定子侧产生和电机位置和转速相关的高频电压或电流信号，通过提取有效信号和解调制等方式得到电机的转速和位置信息。由于没有用到反电动势等受到速度约束的物理两，因此在零低速情况下也有较好的性能。本篇文章主要讲解脉振高频注入法的位置估计原理和实现过程。

2、脉振高频注入位置估计原理

脉振高频注入法通过在同步旋转坐标系的直轴d轴中注入高频正弦电压信号，注入的信号会在静止坐标系中形成一个高频的脉振电压信号，通过对交轴高频电流信号进行幅值调制后，可以提取出其中与转子位置有关的信息，以此方式来获得转子位置速度信息。

其原理框图如下图所示，

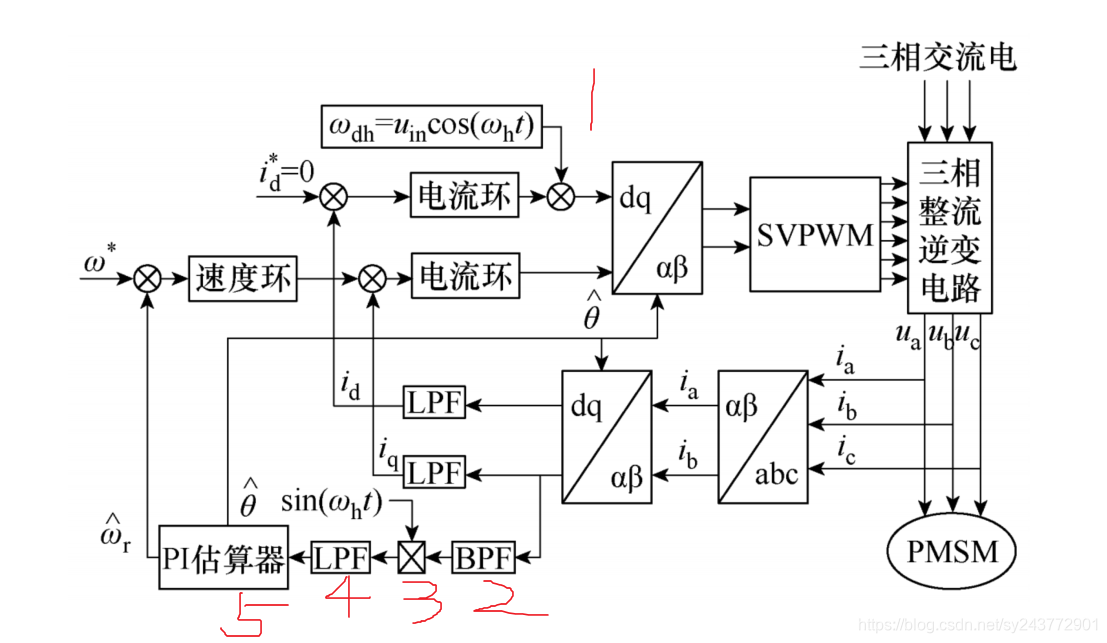
第一步：在d轴注入高频电压信号wdh。高频信号经过电机内部反应可以得到包含位置信息的电流信号，

第二步：通过BPF提取需要的电流信号。由于此信号频率固定，因此经过带通滤波器BPF提取我们需要的频段内电流信号。

第三步：利用乘法器解调制电流信号。对此电流信号进行解调制，通俗的讲就是通过数学运算处理输出的信号。

第四步：通过LPF提取位置估算器所需输入信号。

第五步：经过位置估算器（锁相环）输出位置速度信息。

小结：

高频注入法其实可以比喻为一种化学实验，电机就是我们烧杯内的化学物质，注入高频电压信号就是化学试剂。将化学试剂注入到烧杯中，烧杯内部就会发生化学反应。然后去对化学反应产生的物质进成分提取和分析，来得知烧杯内物质的特性。这种方法可以不依赖电机的反电动势信息，通过注入的信号反应来对电机的位置转速进行估计，能够有效解决电机在零低速环境下位置估计难的问题。

永磁同步电机无速度传感器控制（三）——模型参考自适应法（一）【估计原理】

沉沙丶已于 2022-11-15 20:23:10 修改

本篇对另外一种无速度传感器控制策略做详解——模型参考自适应MRAS无速度控制策略。

1 MRAS简介

MRAS的主要思想：构建两个具有相同物理意义的输出量的模型，其中以不含有位置参数的电机方程作为参考模型，而将待估计参数的方程作为可调模型。利用两个模型输出量差值构建适当的自适应律来实时调节可调模型的参数，使得可调模型的输出跟踪参考模型的输出。MRAS结构图如图所示：

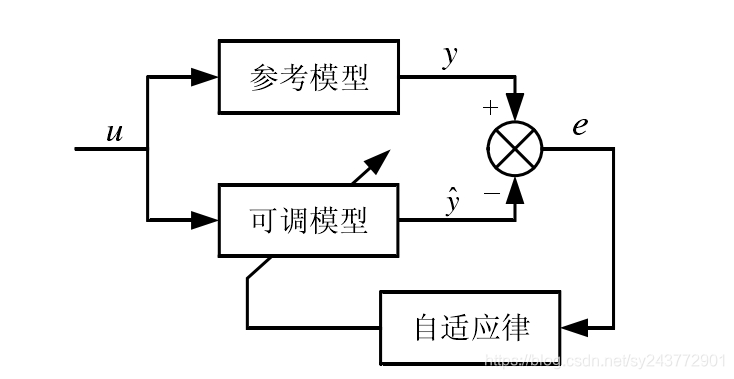
在MRAS转速估计中，系统和转速的渐近收敛由Popov超稳定理论来保证**。对Popov积分不等式逆向求解即可得到由PI调节器控制的转速估算公式**。

2 基于MRAS的PMSM参考模型和可调模型的建立

首先看看PMSM在dq轴坐标系下的数学模型，定子电压方程如下，其中p为微分算子。

定子磁链方程如下：

若将其转换为电流模型，即将定子磁链方程带入到定子电压方程中即可得到以定子电流作为状态变量的电流模型，如下所示：

令 id’= id + phif/L ,，iq’ = iq ，Vd’ = Vd + Rs*phif/L，Vq’ = Vq，

则可以将参考电机模型写为：

将可调模型写为：

3、转速估计的原理

在设计完参考电机模型和可调模型之后，可以结合文章开头所述，利用两个模型输出量的差值构建适当的自适应律来实时调节可调模型参数，使得可调模型输出跟踪参考模型的输出。那么两个模型的输出是什么呢？是电流。调节可调模型的什么参数呢？转速。经过处理的电流差值（后面介绍这里为什么是经过处理的电流差值）经过估算PI调节器后可以得到估算转速we，这个we会驱使可调模型输出的id iq向参考模型的idiq逼近。从而使得可调模型收敛于可调模型，进而可以使得可调模型中的估算转速向实际转速逼近，进而实现转速的估计。

永磁同步电机无速度传感器控制（三）——模型参考自适应法（二）【自适应律的设计】

沉沙丶已于 2022-11-15 20:24:13 修改

1、简写MRAS参考模型和可调模型

参考模型和可调模型方程：

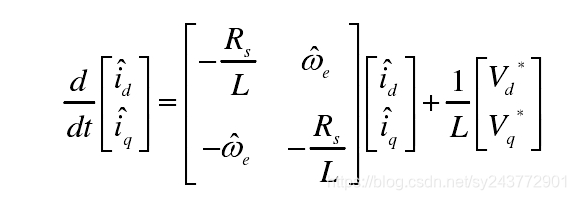
简写为如下形式：

参考模型：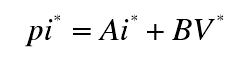

可调模型：

定义广义误差为，
将上述两个方程做差可以得到如下误差方程。

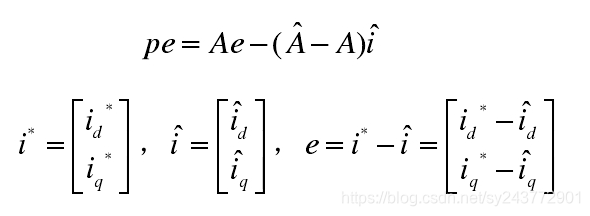
2、改写为标准前向环节

将上式改写为标准前向环节，方便对于Popov超稳定理论的分析。因为Popov超稳定理论规定了以下两个条件：

线性定常环节传递矩阵必须为严格的正实矩阵。
非线性时变反馈环节必须满足Popov积分不等式，即

改写为标准前向环节后的误差方程如下所示：

可以将其表示为下图所示结构：

3、满足Popov超稳定理论的自适应律设计

根据查阅文献可知，对Popov积分不等式逆向求解即可得到MRAS转速估计系统的自适应律。将误差方程带入到Popov积分不等式中时，可以得到：

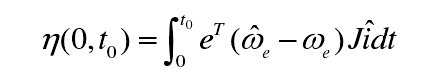
根据MRAS的基本结构，将估算速度we设计为比例积分的形式，

若能够证明此时的 we 是满足Popov超稳定理论，那么其就可以作为自适应律。证明过程如下：

将估计转速we带入到Popov积分不等式：

将其分解为：

如果上面两个均满足大于等于0，那么就可以证明稳定。

因此可以证明we比例积分形式满足Popov超稳定理论。因此可以对此进行自适应律提取：

将上式写成Pi的形式可得：

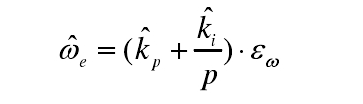
其中：

4、容易出错的点

这里讲一个比较容易出错的点，那就是下面这个方程，具体其id是什么，id^又是什么？

我们经过上面的推导，已经知道MRAS的基本观测原理。但是在这个地方，很多同学被以上物理公式混淆了。按照论文中给的这个公式，iq^就是如下公式设计的。但是其实论文中这么表示，极其的不严谨，此处的 id iq 是实际电机反馈的，那么此处的id^iq也应该是电机反馈电流的估计值。而不是下面两张图这样归一之后的结果：

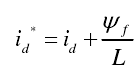
很多同学往往按照如下这张图去搭建MRAS观测器，结果发现怎么出来都不对。

其实事实上我们分析的时候可以这么分析，但是真的搭建仿真的过程中，还是要按照这个方程式来搭建：

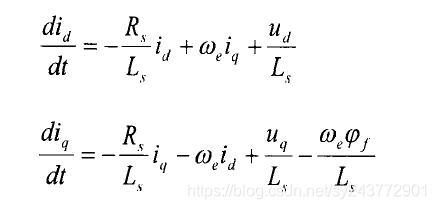
而这个估计出来id^{才是这个公式里面的id}

最后以两张图来证实一下，正确的论文中的写法，两张图来自同一篇论文，所以一定要注意。

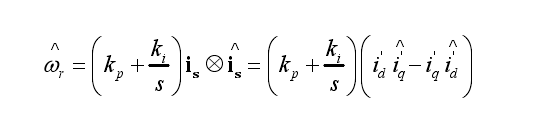
永磁同步电机的I/F启动控制策略

沉沙丶已于 2022-10-18 23:12:14 修改

前言

近年来无速度传感器控制策略得到了深入的研究，按照适用的转速范围可以被分为两类：低速无速度和高速无速度传感器控制策略。低速的方法利用电机的凸极性，注入激励来获得电机的转子位置信息，高频注入的效果当然是较好的，但是也存在噪声，开发难度也相对较大，因此一种较为简单的低速无速度的方法得到了广泛的使用——I/F控制方式。（流频比控制）

一、I/F控制是什么？

I/F控制是根据永磁同步电机负载特性，给变频器设置合适的电流-频率比，使得电机输出转矩与不同转速下的负载相匹配，以达到较高的运行效率。I/F控制策略运行在速度开环、电流闭环的状态，有PI调节器构成DQ轴坐标系下的电流闭环，电流的反馈至收到期望值的约束，避免产生过流。其系统控制框图如下图所示，与有速度传感器控制系统框图存在较大区别：dq轴电流环给定电流idref 与 iqref 均来源于I/f控制器；不存在转速；并且关键一点是Park 变换与反Park 变换的输入位置信号 theta 同样来源于I/F控制器。

如果从数学模型的角度对I/F进行剖析，将更好理解这种控制方式。永磁同步电机在dq轴坐标系下的电磁转矩公式如下所示：

式中Is为定子电流矢量，phim为转子磁链矢量，theta为定子电流矢量和转子磁链矢量之间的夹角

二、永磁同步电机的功角自平衡原理

通过分析数学模型可知，永磁同步电机的输出转矩与定子电流iq分量成正比，控制定子电流的大小就可以控制输出转矩。在电磁转矩和负载相平衡的时候，定子电流Is和转子磁链pihm之间夹角保持固定，并且转子在电流矢量的牵引下同步旋转；如果电磁转矩大于负载转矩，转子加速旋转，夹角theta逐渐减小，电磁转矩也逐渐减小，并在一个新的位置建立转矩平衡；如果电磁转矩小于负载转矩，转子减速旋转，夹角theta逐渐增大，电磁转矩也逐渐增大，同样在一个新的位置建立转矩平衡。如果这个theta角增大超过了90°还是没办法建立平衡，电机将失去稳定平衡，造成失步。

这里就需要详细探究一下了？为什么电磁转矩加速旋转，夹角逐渐减小，能够到一个新的位置建立转矩平衡？为什么theta超过了90°电机将失去稳定平衡，造成失步呢？

这个就回到了上面那个公式上面去了，如果is矢量长度不变，磁链大小不变，电磁转矩Te的输出大小由sin(theta)的大小决定，可以空间想象一下，永磁同步电机的运转本质是定子产生磁动势拖动永磁体旋转，就相当于是我有两个磁铁放地上，我可以控制其中一个旋转，另一个会被这个拖着旋转。在不同的相对位置转动可旋转的磁铁，另一个磁铁跟随旋转的快速性不一样，这就是theta影响的。

那首先研究一下加速过程，假如控制可旋转磁铁开始旋转，并且电流矢量和磁链的初始角度theta = 0°，sin(theta)= 0 ，因此初始的时候没有任何的转矩，可旋转磁铁对被拖动磁铁没有任何作用力，但是随着旋转磁铁的转动，他们之间相对的角度出现了变化，theta就会开始增大，sin（theta）开始变大，因此开始出现转矩。诶，这个时候被拖动磁铁也不一定旋转，他和地面还有摩擦力在阻挠，那么这个theta还会继续增大，直到产生的转矩能够使得克服摩擦力和可旋转磁铁一起转起来。如果到达了 sin(theta)的最大值，拉力还是小于摩擦力，那这个时候就转不起了，也就是无法到达稳定平衡状态了。考虑到加减速两个过程，因此可以得到永磁同步电机I/F启动的可达平衡条件。这个条件就是功角自平衡的范围，超出了这个范围电机的运行将无法到达稳定。这个条件无论是有速度传感器控制，还是I/F开环控制都是符合的，矢量控制由于时时刻刻有位置从传感器传过来，为了保持时刻为最大转矩输出，但是I/F的角度是自己给的，所以就需要考虑这个范围。

三、实现思路

根据上述的分析，在实现的过程中必须满足功角自平衡条件。在仿真过程中，先把电流内环建立好，然后1、给定一个电流Is；2、给定一个转速，并且将转速积分得到角度，给到park变换和反park变换。考虑到以下几点：

1、实际电机运转过程中，需要经历恒加速阶段，不同的电流对应不同的转矩，因此也对应不同的加速度，例如我现在用的电机参数里面，转动惯量 J = 0.003，永磁磁链强度为0.1827，额定电流为10A，极对数为4，额定转矩为10.96N，因此忽略摩擦阻力与空载的情况下，恒加速阶段加速度为10.96*4/0.003 = 14613rad/s^2（这个是电角加速度），电机额定转速为1000rpm，等于104.7rad/s(机械角速度)，418.8rad/s（电角速度），因此到达额定转速的时间是0.0287s。

2、设置输入速度为

3、对电角速度积分，得到位置信号，并将其导入到坐标变换中，看看效果。图中蓝色线条为给定转速，红色为实际转速，可以看到仿真结果实现了I/F的启动。在实现I/F启动的基础上，就可以做高速的无速度传感器控制了。

总结

I/F启动方式是一种转速开环，电流闭环的无速度传感器控制启动方式，这种方式能够提供一种较为容易实现的启动策略。

整体撸一遍PMSM的滑模观测器（SMO）公式+模型+代码

沉沙丶已于 2024-08-20 14:42:11 修改

本篇文章意图记录模观测器代码学习和调试过程。在此先仅考虑表贴式（隐极）电机，即Ld = Lq。

1、电机公式模型及观测器的设计原理

根据前面的一些基础的理解，滑模观测器观测器最终得到角度的方法是对反电动势 Ealpha 和 Ebeta 求取反正切得到的，因此需要分析的数学模型将从矢量控制中dq坐标系转到 alpha-beta 两相静止坐标系中，两相静止坐标系的电压方程如下所示：

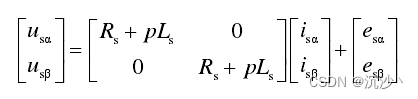
其中反电动势的表达式如下所示：（注意这些分析都是基于表贴式永磁同步电机Ld=Lq，需要研究凸极电机的这个公式并不适用）

由于电压一般进作为激励物理量，而电流才是响应物理量，另外由于电机电流模型中包含常微分方程形式（y’ = f (x,y) ），这种形式的观测器结构更利于稳定性的推导与证明。因此电机中观测器的设计一般是基于电流模型。博客中介绍的MARS其实也是一种电流模型，其稳定性推导就是基于常微分方程展开的popov稳定性理论，滑模也选择这个模型进行。为此将上面两个公式所示的电压模型进行一定的公式变化，得到如下图所示的电流方程：

依据电机模型，等阶次的、格式对应的建立滑模观测器模型，如下所示：

其中观测所得的反电动势表达式如下图所示：

误差方程表达式为（用估测模型 - 实际电机模型）

2、滑模观测器的稳定性分析

一个观测器能否渐进稳定是决定观测器是否能够使用的关键，上面虽然设计了滑模观测器结构，但是它具体能不能够正常使用，还是一个未知的问题。因此有必要对齐进行稳定性证明。稳定性的证明需要用到李雅普诺夫稳定性理论中的稳定性判据。

李亚普诺夫稳定性理论基于李亚普诺夫函数的概念，该函数是一个实值函数，能够度量系统状态的变化情况。根据李亚普诺夫函数的性质，可以推导出系统的稳定性条件。如果李亚普诺夫函数对于系统的所有状态都是非正的，并且在系统中存在一个李亚普诺夫函数值为零的稳定点，那么系统就被认为是稳定的。

简单来说，如果平衡状态 x 受到扰动后，仍然停留在 x 附近，我们就称 x 在李雅普诺夫意义下是稳定的（Lyapunov stable）。

更进一步，如果平衡状态 xe 受到扰动后，最终都会收敛到 x ，我们就称 x 在李雅普诺夫意义下是渐进稳定的（Asymptotically stable）。

再进一步，如果平衡状态 x 受到任何扰动后，最终都会收敛到 x ，我们就称 x 在李雅普诺夫意义下是大范围内渐进稳定的（Asymptotically stable in large）****。

由于滑模是基于开关函数的，因此滑模观测器并不属于一种线性系统，属于非线性系统。因此应用李亚普诺夫第二法较为合适（李亚普诺夫第一方法需要讨论线性化系统的特征值分布来研究原非线性系统的稳定性问题，这是一种间接的证明方法也称间接法）。李亚普诺夫第二法的判据为：

李亚普诺夫第二法则：对于连续时间系统，如果存在一个连续可微的李亚普诺夫函数V(x)，满足以下两个条件：
- V(0) = 0，当且仅当 x = 0 时成立。
- V(x) > 0，对于所有 x ≠ 0 成立。
- 对于系统的状态变化，V(x) 的导数满足 dV(x)/dt < 0，即 V(x) 随时间递减。
则系统是渐近稳定的。总结成方程形式就是

通过李亚普诺夫第二法则，能够证明稳定的系统能量总是不断被耗散的，李雅普诺夫通过定义一个标量函数 V(x)（通常能代表广义能量）来分析稳定性。这种方法避免了复杂的方程求解和线性化，直接证明系统的稳定性，因此称为直接法。对于滑模观测器（其他观测器也类似），稳定判据中的V(x)其实就是误差函数。因为误差函数代表了系统的熵增和熵减，对应李亚普诺夫函数的能量耗散原理。

误差函数为：

根据电流方程及电流误差方程：

可以推出：

β轴的与此同理，满足下面条件即可证明稳定性：

由于平方项必定大于0，因此得到如下推导：

最终得到系统稳定的条件为

这样就能产生滑动运动，这样误差动态方程就是渐进稳定的，也就保证了滑模观测器的全局稳定性，用起来就不担心。

3、连续域仿真模型的搭建

3.1 滑模前期的仿真基础

依据上述阐述的原理对仿真模型进行搭建，验证算法的有效性。首先需要准备一个基础的双闭环仿真，先尝试用实际速度做闭环时，滑模是否能够估计到真实转速。电机参数如下图所示。

3.2 搭建滑模观测器

在此基础上搭建滑模观测器，避免大家上面再去翻，再次粘贴一次公式：

3.3 滑模参数调试

滑模观测器中除了电机参数需要填入外，还需要填入两个关键参数——滑模增益和低通滤波器截止频率。由于本文所使用的电机母线电压只有24V，反电动势比不可能大于24，根据前文稳定性推导部分可知，设置滑模增益为24系统必定处于全局可收敛。本仿真系统的开关频率时10kHz，电机额定频率为250Hz，因此考虑设置滑模后端的低通滤波器为中间值即1000Hz（1000Hz对应的wc = 10002pi = 6280）。带入上述参数进行调试，下图为观测所得Ealpha和Ebeta波形。

根据上图所示波形，可知该滑模观测器已基本实现反电动势波形的观测，但是明显可以看到此时的波形毛刺较大，抖振较为严重，考虑降低滑模增益调试。初始给定的24V仅仅是一个较为保守的值，将其缩小根号3倍，即 24/1.732 = 13.85。该滑模增益时反电动势波形如下图所示，此时抖振已被减小的较小了。

此时仍然存在的一些谐波是滑模观测器自身在上下滑动过程中造成的，并非滑模增益设置不够合适，而是低通滤波器的截止频率可能太高了，许多谐波没有被滤掉。因此考虑降低低通滤波器的截止频率到2倍额定频率 = 250Hz2 = 500Hz，将其转化为wc = 5002*pi = 3140。反电动势波形如下图所示，其实调到如下程度就可以了，可进行转速和位置的提取。

3.3 袁雷书上SMO_acrtan模型存在的一点遗漏

刚开始看书的时候发现这个地方怎么也看不懂，经过大佬的指导发现这里存在一些问题，**（感谢千羽同学提供的一些思路）**将其总结如下面4个，后续3.4部分探究解决过程。具体的如下图所示，袁雷书上模型的链接如下：

链接：https://pan.baidu.com/s/1FIrezc-PAqBylqqVvO0IaA

提取码：8888

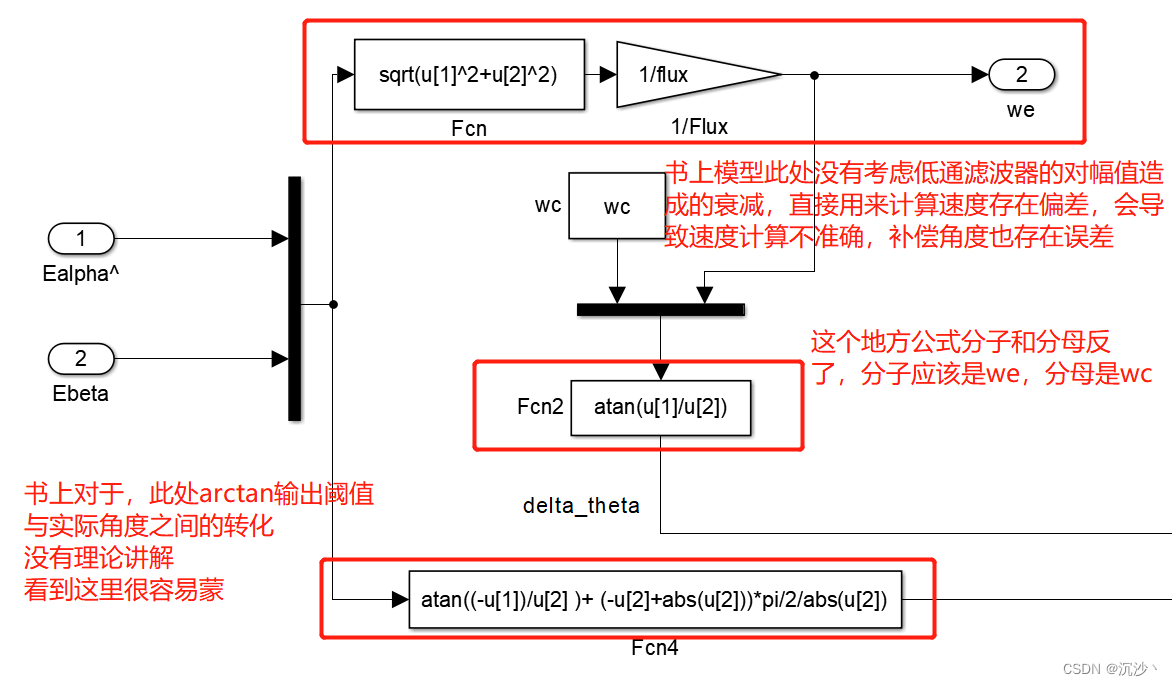
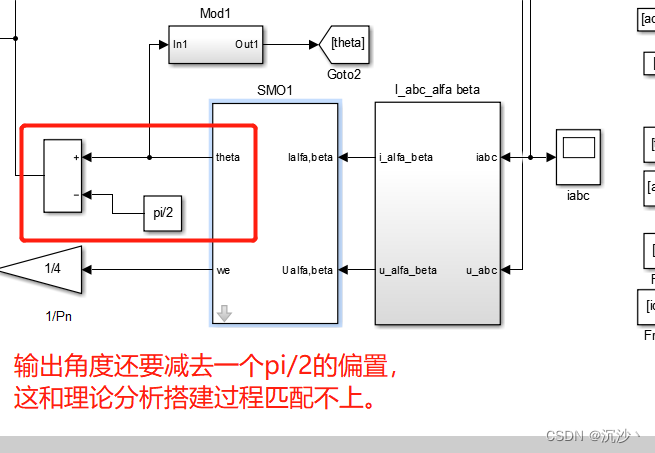
3.4 重新推了一下基于反正切函数的转子位置角度提取

根据电机反电动势表达式，对反电动势求反正切即可得到电机的角度信息。

电机转子位置表达如下所示：

搭建仿真实现其过程，仿真模块搭建如下图所示：

 此时将电机转子位置角与滑模估算角度放在一个示波器中进行观察，如下图所示，此时波形非常的奇怪，电机位置角（红色）一直在累加，这是因为simulink仿真自带的PMSM模块出来的电角度就是会一直叠加，为此我们需要在其前级加上一个取余函数。编写一个s-function或者搭建一个取余模块，为什么这里写出来呢，因为我在这里被坑了好久，有的版本找不到mod模块，最好用s-function写一个mod()函数的处理一下。

 最终得到的转子位置对比图如下图所示：

 由于arctan函数的输出值（-pi/2，pi/2），其函数图像如下图所示。

需要具体的分析 arctan函数输出值与实际电机位置角的关系，当acrtan(-Ealpha /Ebeta) =  1时，实际存在两个可能的结果，一个是pi/4，一个是5pi/4，因为sin(pi/4) = 0.707  ,cos(pi/4)=0.707，但是sin(5pi/4)=-0.707，cos(5pi/4)=-0.707。因此仅凭acrtan(-Ealpha /Ebeta) =  1无法确定具体是pi/4还是5pi/4，根据一系列推论总结可得（下面这个公式其实就是通过每个象限的值一一枚举然后总结出来的，就把1 2 3 4  象限的不同的值和 arctan 的输出值相互对应出来的）

其模块代码为：

function y = fcn(Ealpha,Ebeta,Acrtan)
%#codegen
x = 0;
if Acrtan > 0 
    if Ebeta < 0
        x = pi + Acrtan;
    elseif  Ebeta > 0
        x =  Acrtan;
    elseif Ebeta == 0
        x = 0.5*pi;
    end
elseif Acrtan<0
    if Ebeta < 0
        x = pi + Acrtan;
    elseif  Ebeta > 0
        x = 2*pi + Acrtan;
    elseif Ebeta == 0
        x = 1.5*pi;
    end
elseif Acrtan == 0
     if Ebeta < 0
        x = pi;
    elseif  Ebeta > 0
        x = 0;
     elseif Ebeta == 0
        x = 0;
    end       
end
y = x;

最终结果对比，蓝色为滑模观测器结果，黄色为电机实际角度，可以看到基本一致，由于低通滤波器的存在，有一定的延迟。

低通滤波器造成的延迟会影响电机转子位置的准确性，因此需要对这个延迟进行一定的补偿，其实低通滤波器的截止频率我们是知道的，补偿这个延迟理论上是较好进行的。j将低通滤波器的传递函数转化为幅频和相频公式可得：

 将滑模所用的低通滤波器传递函数转换一下可得：

 其相位延迟等于：

 最终得到补偿相位公式为：

 将其补偿到输出电机角度上后结果如下图所示，估算角度基本与实测电机角度重合。但是此时我的补偿角度是拿电机实际we算出来的，所以波形效果相当好。（注意这里如果直接补偿上去，会导致出现大于2pi的角度，此时就需要稍微处理一下，把超出2pi的角度转为小角度，也就是减去2pi即可）

 实际是需要通过反电动势去算取we，其计算公式为：

 最终观测输出结果如下图所示，效果也是挺好的。

整体获取角度+补偿过程的仿真截图如下图所示

最终实现转速闭环控制效果如下图所示：

四、滑模观测器的离散化

仿真中可以按照连续模型去搭建，在代码中则必须考虑MCU的离散环境，先看连续域的电机电流方程，如下图所示。式子中 R  代表定子电阻，L 为定子电感，Valpha 为两相静止坐标系下的alpha 电压，ealpha 为两相静止坐标系下的 alpha 反电动势。根据 ealpha 和 ebeta 的表达式可知假如能够观测反电动势的大小，对齐求反正切即可得到电机电角度信息。

依据前向欧拉方程进行离散化推导，离散化操作可参照这篇文章。

数字滤波器的实现——低通滤波器再探究

沉沙丶已于 2024-11-11 22:32:29 修改

在探究完滤波器原理之后，又面临一个问题就是数字滤波器如何实现的问题，因为在实际应用过程中，如果不接触硬件的话，低通滤波器一般都是通过编程实现的，具体代码应该怎么编写，在应用过程中又应该注意什么问题呢？这里值得探究一下。

首先我们回顾一下低通滤波器的原理：

从自动控制原理的角度，一阶低通滤波器实际上是一个一阶惯性环节，低通滤波器的传递函数表达形式如下所示，即为一阶惯性环节的传递函数表达式，截止频率为1000rad/s。

那如果放在代码里面如何实现呢？

第一步：求取滤波器的差分方程，需要按照下述流程。S域传递函数——Z域离散函数——差分方程。

假设当前S域传递函数为：

**通过后向差分方法，对其离散化，**还有前向差分和双线性变换法，其中前向差分法不稳定，双线性变换精度更高，这里先探究一种；后向差分法中s算子的表达式为：

$\Large s=\frac{1-\mathop{z}^{-1}}{T}=\frac{z-1}{\mathop{T}_{z}}$

式中T为离散化过程中的单个步长时间，通常在单片机中是采样周期或为中断周期。可以得到离散域的传递函数：

由于在信号传递过程中：

即：

将其带入整合得到的输入输出关系式中，可以得到差分方程表达式：

若传递函数为文中开始的形式：

式中T为离散化过程中的单个步长时间。再次执行一下上面的推导过程；

经过推导后可以得出差分方程表达式为：

第二步：编程实现

有了差分方程，下一步就是对其进行编程实现，插入一个function模块，代码段为：

function y = fcn(u)
%#codegen
persistent yk yk_1 Tsc wc
if isempty(yk)
    yk = 0;
    yk_1 = 0;
    Tsc =0.0001;
    wc =100;
end
 sum = (1+wc*Tsc);
    alpha = 1 / sum
    beta = wc*Tsc / sum
    yk = alpha*yk_1 + beta*u;
    yk_1 = yk;
y = yk;

如果按照文中开头给的传递函数，基波为幅值为100，角频率为10rad/s的正弦波，噪声是幅值为10，角频率为1000rad/s的正弦波。低通滤波器的截止频率100rad/s，采样时间为0.001s。对其进行仿真实验，下图第一行为原始波形，第二行为连续域传递函数滤波后效果，第三行为数字滤波器滤波后效果，可以看到，通过上述函数实现了对高频噪声的滤除，实现了指定截止频率的低通滤波器，代码具备实际应用价值。

附件：绘制截止频率为 100 rad/s的低通滤波器在连续域与离散域的bode图。

% transfor function
sys = tf([100], [1 100]);
 
% discretize
ts = 0.0001; % 采样周期
dsys = c2d(sys, ts, 'i'); % 转化为差分方程
 
% extract
[num, den] = tfdata(dsys,'v'); % 提取差分方程系数
sys =sys
dsys = dsys
opts = bodeoptions;
opts.FreqUnits = 'rad/s';
opts.XLim = [0.01, 10000];
opts.Grid = 'on';
 
bode(sys,dsys,opts);

第三步：通用性低通滤波器的代码撰写

实际上在公司的代码里面，是不会直接对截止频率进行给定的，当然我认为直接给截止频率更方便一些，为了适应工作环境，下面附上按照滤波常数 Tf 和采样时间 Tsc 来设计低通滤波器的函数。

function y = fcn(u)
%#codegen
persistent yk yk_1 Tsc Tf
if isempty(yk)
    yk = 0;
    yk_1 = 0;
    Tsc =0.0001;
    Tf =0.01;
end
    alpha =  Tsc / (Tsc+Tf)
    beta = Tf / (Tsc+Tf)
    yk = (u * Tsc + yk_1*Tf )/(Tsc+Tf);
    yk_1 = yk;
y = yk;

截止频率 wc 和滤波常数 Tf 之间的比例关系如下所示：

按照滤波时间常数 Tf 设计的滤波器结果如下图所示，输入和噪声与上文一致，从图中可以看出已实现了低通滤波器的功能。

任意低通滤波器传递函数转换为代码的一种方法：

% transfor function
sys = tf([100], [1 100]);
 
% discretize
ts = 0.0001; % 采样周期
dsys = c2d(sys, ts, 'i') % 转化为差分方程

转化为这个结果

基于这个结果推导一下公式：

输入代码：例如SMO的反电动势滤波，输入为Zalpha，输出为Ealpha。由于代码是顺序执行，等号右侧的Ealpha实际上是上一次进入中断算出的Ealpha值。

Ealpha = 0.99Ealpha + 0.01Zalpha;

为了便于显示当然也可以写成：这样在最后把Ealpha赋值给另一个变量，更加直观易读，但是也会多出一个变量定义。

Ealpha = 0.99Ealpha_old + 0.01Zalpha; 
.....//其他代码
Ealpha_old = Ealpha;

20241111补充：

高版本的脚本计算出来的结果如下：

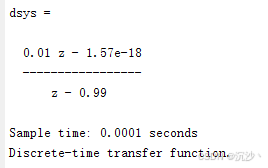
忽略后续1.57e-18即可

via:

永磁同步电机矢量控制基础补充（一）——如何绘制电机输出的磁链_电机磁链-优快云博客
https://blog.youkuaiyun.com/sy243772901/article/details/104653596
永磁同步电机矢量控制基础补充（二）——Matlab自带坐标系和书本自然坐标系之间的关系_rotor flux position when theta = 0-优快云博客
https://blog.youkuaiyun.com/sy243772901/article/details/104797288
永磁同步电机矢量控制基础补充（三）——如何理解调制度m_调制度和调制比-优快云博客
https://blog.youkuaiyun.com/sy243772901/article/details/105067141
永磁同步电机矢量控制基础补充（四）——如何设定电流环PI调节器和转速环PI调节器的限幅值_速度调节器的输出限幅值如何整定-优快云博客
https://blog.youkuaiyun.com/sy243772901/article/details/105287993
永磁同步电机矢量控制基础补充（五）——什么是低通滤波器？_截止频率的单位是什么-优快云博客
https://blog.youkuaiyun.com/sy243772901/article/details/105497574
永磁同步电机矢量控制基础补充（六）——如何在simulink初始化电机参数？_simulink如何初始化参数-优快云博客
https://blog.youkuaiyun.com/sy243772901/article/details/105947207
永磁同步电机矢量控制基础补充（七）——模块化解释永磁同步电机PMSM的矢量控制_矢量控制原理图-优快云博客
https://blog.youkuaiyun.com/sy243772901/article/details/105703596
永磁同步电机矢量控制基础补充（八）——Matlab/Simulink打开仿真出现的问题汇总_设计电机没有足够的空间容纳bs0怎么解决-优快云博客
https://blog.youkuaiyun.com/sy243772901/article/details/106195484
永磁同步电机矢量控制基础补充（九）——Simulink软件的入门学习_学习驱动电机矢量控制技术的软件-优快云博客
https://blog.youkuaiyun.com/sy243772901/article/details/106027149
永磁同步电机矢量控制基础补充（十）——调制模式和控制方式之间的区别？_同步调制 pmsm-优快云博客
https://blog.youkuaiyun.com/sy243772901/article/details/106716343
—
永磁同步电机无速度传感器控制（一）——滑模观测器（一）【位置估计原理】_无位置传感器永磁同步电机位置估计-优快云博客
https://blog.youkuaiyun.com/sy243772901/article/details/107029214
永磁同步电机无速度传感器控制（一）——滑模观测器（二）【滑模观测器设计过程】-优快云博客
https://blog.youkuaiyun.com/sy243772901/article/details/107071917
永磁同步电机无速度传感器控制（一）——滑模观测器（三）【由扩展反电势得到电机位置和速度信息】_扩展反电动势-优快云博客
https://blog.youkuaiyun.com/sy243772901/article/details/107133633
永磁同步电机无速度传感器控制（一）——滑模观测器（四）【仿真搭建及其结果分析】_无速度传感器转速波形-优快云博客
https://blog.youkuaiyun.com/sy243772901/article/details/107291663
永磁同步电机无速度传感器控制（一）——滑模观测器（四）【仿真搭建及其结果分析】_无速度传感器转速波形-优快云博客
https://blog.youkuaiyun.com/sy243772901/article/details/107291663
永磁无速度传感器_沉沙丶的博客-优快云博客
https://blog.youkuaiyun.com/sy243772901/category_8885491.html
永磁同步电机无速度传感器控制（二）——脉振高频注入法（一）【位置估计原理】_永磁同步高频注入原理-优快云博客
https://blog.youkuaiyun.com/sy243772901/article/details/107780148
永磁同步电机无速度传感器控制（三）——模型参考自适应法（一）【估计原理】_永磁同步电机基于增益因子的模型自适应控制-优快云博客
https://blog.youkuaiyun.com/sy243772901/article/details/107944883
永磁同步电机无速度传感器控制（三）——模型参考自适应法（二）【自适应律的设计】_自适应律怎么设计-优快云博客
https://blog.youkuaiyun.com/sy243772901/article/details/107946469
永磁同步电机的I/F启动控制策略_if启动-优快云博客
https://blog.youkuaiyun.com/sy243772901/article/details/119323833
数字滤波器的实现——低通滤波器再探究_低通滤波器传递函数-优快云博客
https://blog.youkuaiyun.com/sy243772901/article/details/119732233
整体撸一遍PMSM的滑模观测器（SMO）公式+模型+代码_滑膜观测器-优快云博客
https://blog.youkuaiyun.com/sy243772901/article/details/131270372