Matlab:利用势能法和切片法编写关于斜齿轮时变啮合刚度求解模型的Matlab程序，根据端面和轴面重合度的大小比较

Matlab:利用势能法和切片法编写关于斜齿轮时变啮合刚度求解模型的Matlab程序，根据端面和轴面重合度的大小比较，分为了两种计算方法，以此作为计算，然后根据周期变化计算得到整个啮合过程的综合刚度啮合曲线，并得到拟合公式！ 内含详细解答

MATLAB 代码和参考文献《斜齿轮时变啮合刚度算法修正及影响因素研究》撰写的功能说明文章，适用于技术报告、项目文档或学术论文中的方法介绍部分。

---

一、研究背景

斜齿轮传动系统在高速、重载工况下表现出良好的平稳性和承载能力，其时变啮合刚度是引起系统振动与噪声的主要激励源之一。准确计算斜齿轮的时变啮合刚度，对齿轮系统的动态特性分析、故障诊断与减振设计具有重要意义。

传统的势能法在计算斜齿轮啮合刚度时，往往忽略齿根圆与基圆不重合的影响，导致计算误差较大。本文基于切片法与势能法，结合重合度分段模型，提出了一种修正的斜齿轮时变啮合刚度计算方法，并通过 MATLAB 实现。

二、方法原理

2.1 势能法与切片法基础

将斜齿轮齿面沿齿宽方向切分为若干薄片，每片视为一个变截面悬臂梁。在啮合过程中，各片依次进入和退出啮合，总刚度为各片刚度的并联组合。

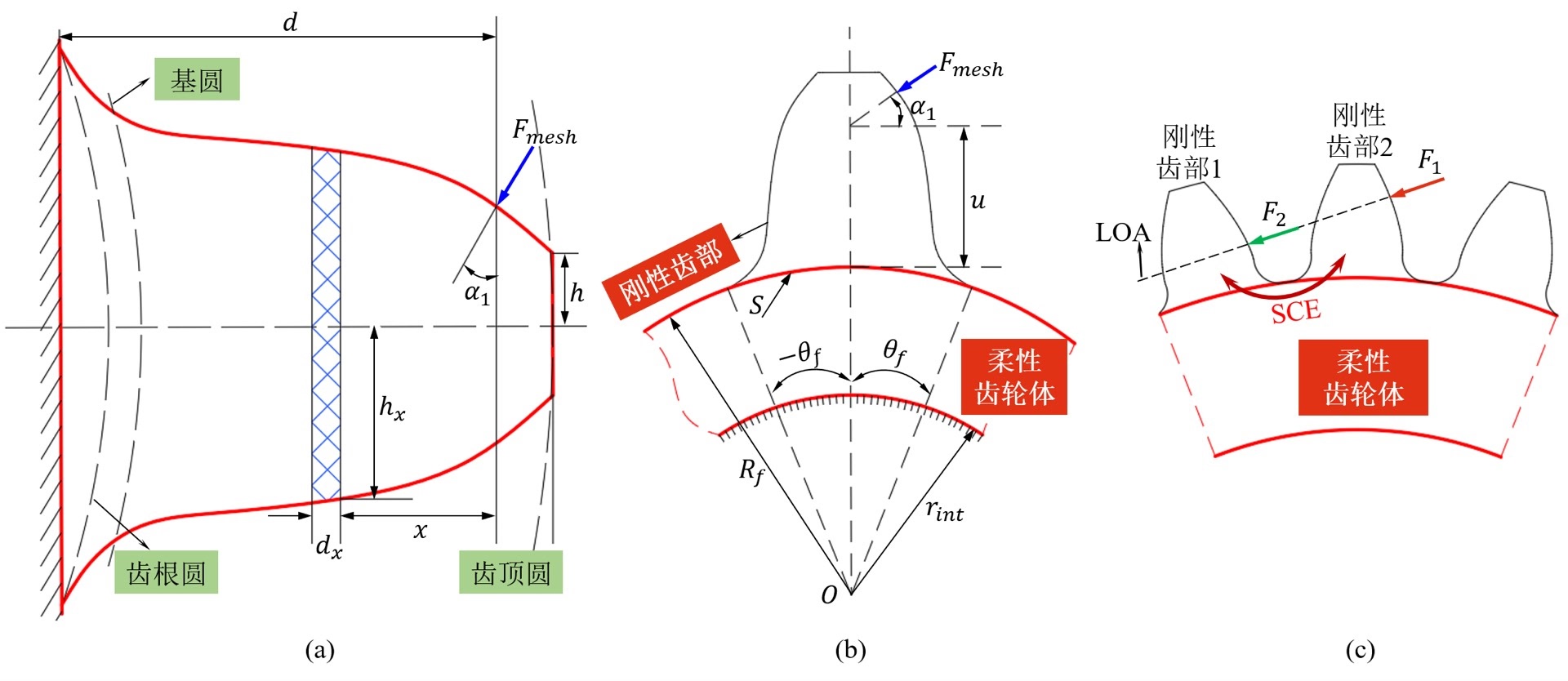
斜齿轮的啮合刚度包括：

• 赫兹接触刚度 \( k_h \)
• 弯曲刚度 \( k_b \)
• 剪切刚度 \( k_s \)
• 轴向压缩刚度 \( k_a \)
• 基体刚度 \( k_f \)

总刚度计算公式为：

\[

\frac{1}{k} = \frac{1}{kh} + \sum \left( \frac{1}{k{b}} + \frac{1}{k{s}} + \frac{1}{k{a}} + \frac{1}{k_{f}} \right)

\]

2.2 重合度分段模型

根据端面重合度 \( \varepsilon\alpha \) 与轴向重合度 \( \varepsilon\beta \) 的大小关系，将单齿啮合过程分为三个阶段：

1. 啮入段：接触线长度线性增加
2. 稳定段：接触线长度保持最大
3. 啮出段：接触线长度线性减小

2.3 齿根圆与基圆不重合的修正

传统模型将齿根简化为基圆起始的悬臂梁，忽略了齿根圆与基圆之间的过渡区域。本文通过分段积分方法，分别计算基圆以上和基圆以下部分的变形能，显著提高了刚度计算精度。

三、MATLAB 程序功能说明

3.1 主要模块

（1）`stiffness1.m`：单齿啮合刚度计算

• 输入齿轮参数（齿数、模数、螺旋角、压力角、齿宽等）
• 根据重合度大小判断计算方法（\( \varepsilon\alpha > \varepsilon\beta \) 或 \( \varepsilon\alpha < \varepsilon\beta \)）
• 分三个阶段计算接触线长度与各刚度分量
• 输出单齿在一个完整啮合周期内的刚度曲线

（2）`matr2_gangdu_pingyi_stiff.m`：综合刚度合成与拟合

• 将单齿刚度曲线进行周期平移叠加，得到多齿啮合的综合刚度
• 使用傅里叶级数对综合刚度曲线进行拟合，得到解析表达式
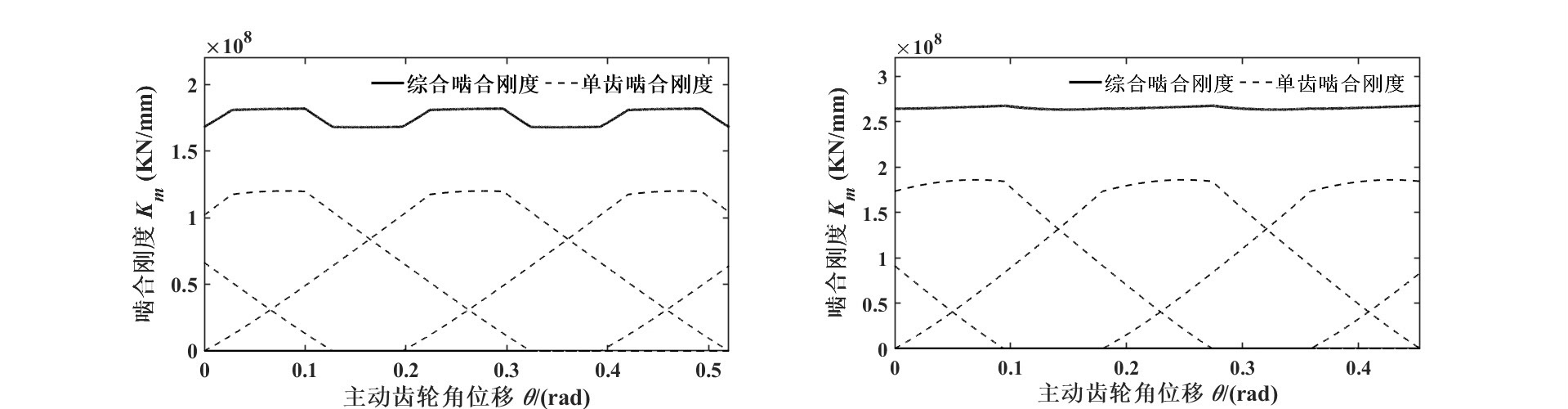
• 绘制单齿刚度与综合刚度对比图

3.2 关键技术点

• 切片数可调：N=1000，可根据精度需求调整
• 重合度自适应：自动判断端面与轴向重合度大小，选择相应算法
• 基圆修正：考虑齿根圆与基圆不重合的影响
• 傅里叶拟合：提供两种拟合公式，便于后续动力学建模使用

四、输出结果

程序输出包括：

1. 单齿啮合刚度曲线（分三个阶段）
2. 综合啮合刚度曲线（多齿叠加）
3. 拟合公式（傅里叶级数形式），例如：

\[

K(t) = a0 + \sum{n=1}^6 \left[ an \cos(n\omega t) + bn \sin(n\omega t) \right]

\]

五、应用价值

本模型适用于：

• 斜齿轮系统动态响应分析
• 齿轮箱振动与噪声预测
• 齿轮参数优化设计
• 故障齿轮刚度退化建模

六、参考文献

刘文, 李瑞, 张金红, 等. 斜齿轮时变啮合刚度算法修正及影响因素研究[J]. 湖南大学学报（自然科学版）, 2018, 45(2): 1–10.

---