VIO残差函数构建
带权重(方差)的残差计算:,其中f(x)服从高斯分布,协方差为
协方差可以将所有残差变化到一个统一的无量纲的范围内,可以将不同残差进行相加
协方差还能起到一个权重的作用,协方差越小,则它的逆就越大,该测量值就更可信
基于滑动窗口的VIO Bundle Adjustment


为了节约计算量采用滑动窗口形式的Bundle Adjustment, 在 i时刻,滑动窗口内待优化的系统状态量定义如下:

其中,xi包含i时刻IMU机体的在惯性坐标系中的位置,速度,姿态,以及IMU机体坐标系中的加速度和角速度的偏置量估计
n,m分别是机体状态量,路标在滑动窗口里的起始时刻。
N滑动窗口中关键帧数量
M是被滑动窗口内所有关键帧观测到的路标数量
视觉重投影误差
定义:一个特征点在归一化相机坐标系下的估计值和观测值的差
,其中,待估计的状态量为特征点的三维空间坐标(x,y,z)T,观测值(u,v)T为特征在相机归一化平面的坐标。
逆深度参数化:特征点在归一化相机坐标系与在相机坐标系下的坐标关系为:
,其中
=1/z是逆深度。
VIO中基于逆深度的重投影误差:特征点逆深度在第i帧中初始化得到,在第j帧又被观测到,预测其在第j中的坐标为
相机坐标系c1→body坐标系b1→body坐标系b2→相机坐标系c2
视觉重投影误差为:
IMU测量值积分:

上标g表示gyro,a表示acc,w表示在世界坐标系world,b表示imu机体坐标系body
PVQ对时间的导数为:
,
,
从第i时刻的PVQ对IMU的测量值进行积分得到第j时刻的PVQ:(前面第一次笔记已经推导过)

用此种方法 ,每次
优化更新后,都需要重新进行积分,计算量大,所以采用预积分的方法
IMU预积分
一个很简单的公式转换,就可以将积分模型转为预积分模型:
那么,PVQ积分公式中的积分项则变成相对于第i时刻的姿态,而不是相对于世界坐标系的姿态

预积分量:预积分量仅仅跟IMU测量值有关,它将一段时间内的IMU数据直接积分起来就得到了预积分量

重新整理得到:

预积分误差:一段时间内IMU构建的预积分量作为测量值,对两时刻之间的状态量进行约束,

其中,位移、速度和偏置都是直接相减得到,第二项是关于四元数的旋转误差,其中[]xyz表示只取四元数的虚部(x,y,z)组成的三维向量。
预积分的离散形式
使用mid-point方法,两个相邻时刻k到k+1的位姿是用两个时刻的测量值a,w的平均值来计算

预积分量方差的计算
协方差的传递:已知一个变量y = Ax,,则
假设已知相邻时刻误差的线性传递方程:
误差的传递由两部分组成:当前时刻的误差传递给下一时刻,当前时刻测量噪声传递给下一时刻。
协方差矩阵可以通过递推计算得到:,其中
是测量噪声的协方差矩阵,方差从i时刻开始进行递推,
= 0
状态误差线性递推公式的推导
通常对于状态量之间的递推关系是非线性的方程,如,其中状态量为x,u是系统的输入量
用两种方法来推导状态误差传递的线性递推关系:
一种是基于一阶泰勒展开的误差递推方程
一种是基于误差随时间变化的递推方程
基于一阶泰勒展开的误差递推方程
令状态量为,其中真值为
,误差为
,另外输入量u的噪声为n
基于泰勒展开的误差传递(应用于EKF的协方差预测):
非线性系统的状态误差的线性递推关系如下:
,其中F是状态量xk对状态量xk-1的雅克比矩阵,G是状态量xk对输入量uk-1的雅克比矩阵
证明:进行一阶泰勒展开有

其中,,所以两边可以约掉,即可导上述递推关系。
基于误差随时间变化的递推方程
如果我们能够推导状态误差随时间变化的导数关系,比如
则误差状态的传递方程为:
通过这两种推导方式可以看出:,
为什么会要弄误差随时间的变化呢?
这是因为VIO系统中已经知道了状态的导数和状态之间的转移矩阵,如我们已经知道了速度和状态量之间的关系:
那么就可以推导速度的误差和状态误差之间的关系,再每一项上都加上各自的误差就有:
由此就可以类推,轻易写出整个A和B其他方程了。
预积分的误差递推公式推导:回顾预积分的误差递推公式,注意:这里白噪声用符号+,表示噪声影响状态量,因为白噪声的值无法像bias一样估计,所以没办法减去白噪声

预积分误差传递的形式:用一阶泰勒展开的推导方式,我们希望能推导出误差的递推公式

F,G为两个时刻的协方差传递矩阵,表示各时刻的误差
我们直接给出F,G的最终形式,

其中系数为:
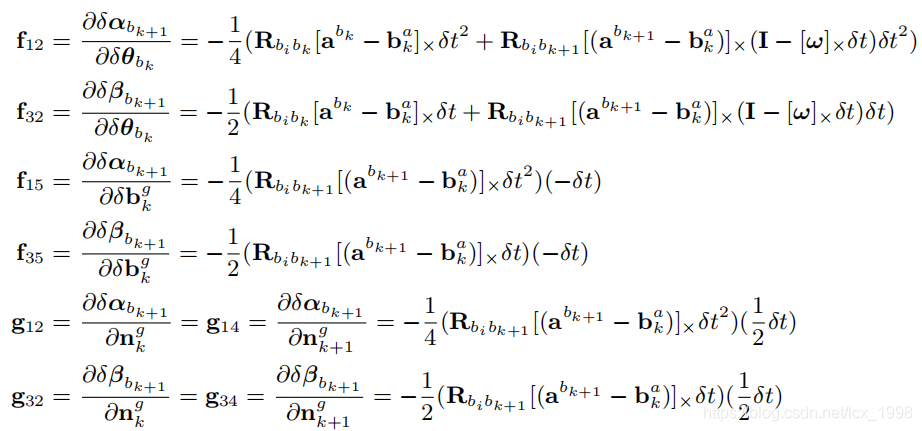
雅克比矩阵F,G的推导
公式简化约定:为了对求导公式进行简化,做一些简单约定,比如求导公式

因为后面那一项与无关。
β对各状态量的雅克比推导,即F的第三行:
速度预积分量β的递推计算形式:

f33:对上一时刻速度预积分量的Jacobian

f32:对角度预积分量的Jacobian
速度的预积分量对角度预积分量误差的Jacobian只跟加速度项有关:



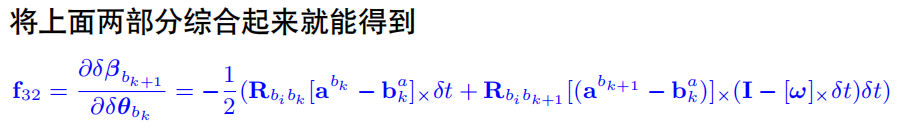
f35:速度预积分量对k时刻角速度的bias的Jacobian

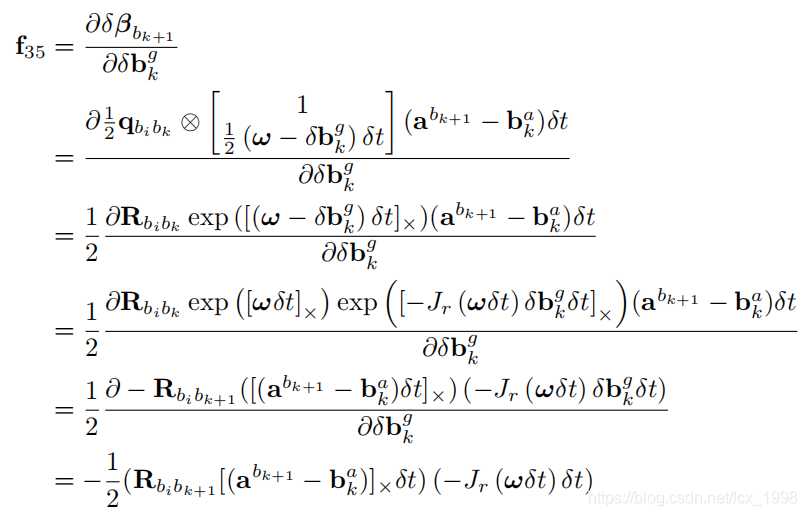
旋转预积分量的Jacobian,即F第二行
旋转预积分的递推公式为:

f22:前一时刻的旋转误差如何影响当前旋转误差








 博客围绕VIO残差函数构建展开,介绍带权重的残差计算,协方差作用。阐述基于滑动窗口的VIO Bundle Adjustment,分析视觉重投影误差,包括定义、逆深度参数化等。还讲解IMU预积分,将积分模型转为预积分模型,最后介绍预积分量方差的计算及误差递推公式推导。
博客围绕VIO残差函数构建展开,介绍带权重的残差计算,协方差作用。阐述基于滑动窗口的VIO Bundle Adjustment,分析视觉重投影误差,包括定义、逆深度参数化等。还讲解IMU预积分,将积分模型转为预积分模型,最后介绍预积分量方差的计算及误差递推公式推导。


















 2154
2154

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








