【深蓝学院】手写VIO第3章--基于优化的VIO（LSP求解，IMU预积分，Jacobian推导）--笔记

0. 内容

1. 基于BA的VIO融合

优化的方法学会之后，滤波的方法也就会了。

具体的求解BA问题参考的是SBA的论文，使用的是LM算法（里面有个关于权重μ的计算方法，不同人的实现可能不一样，这些都是实现细节）

camera两个观测之间的相对位置（pq的变化）可以通过两次观测知道，但是IMU在两个时刻的观测量需要进行积分才能知道，而且IMU数据频率一般比Camera频率高，所以需要逐步地积分才能得到运动情况。

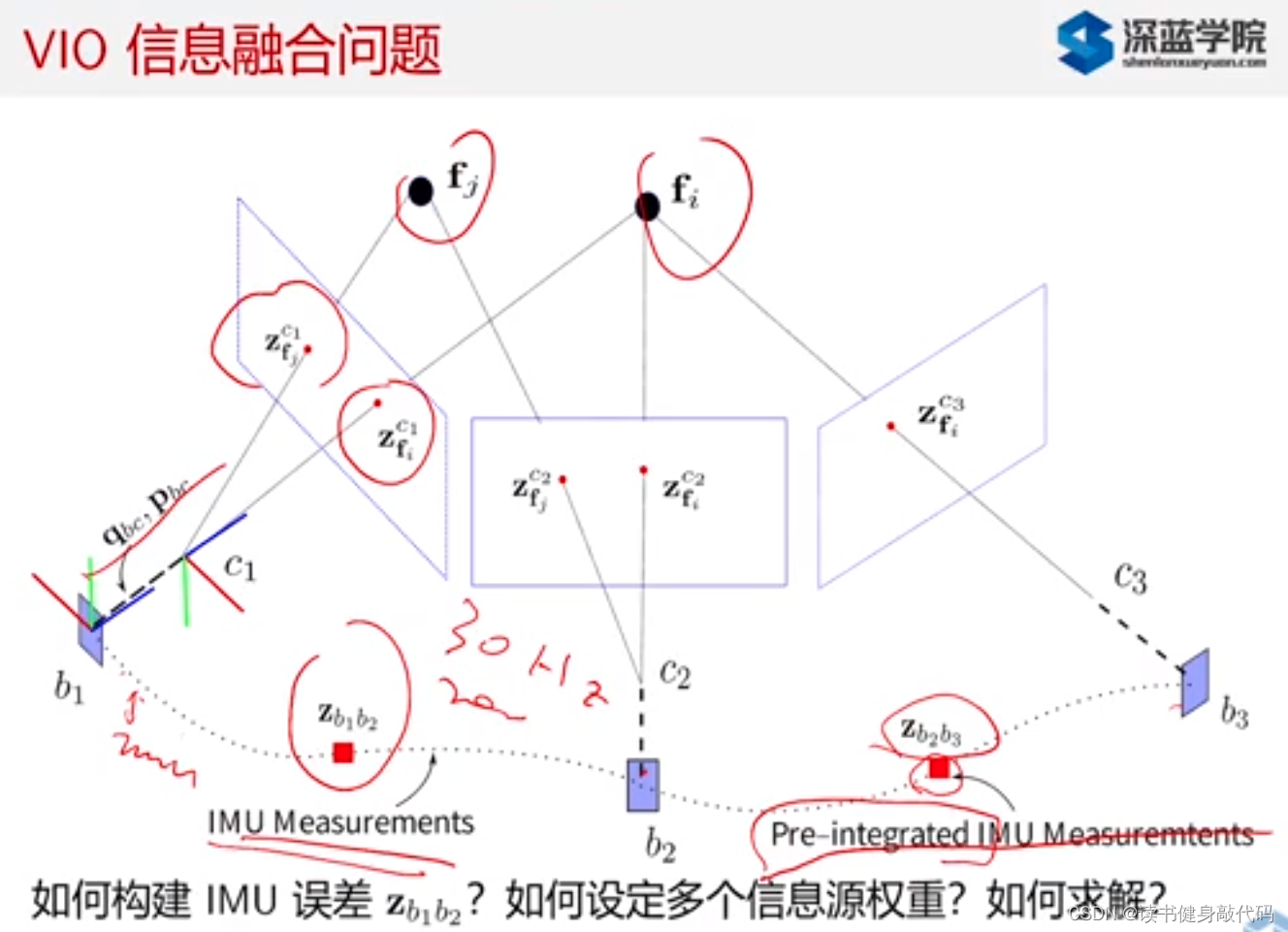
2. 最小二乘问题的求解

牛顿法，将loss function直接Taylor二阶展开，高斯牛顿法是将原函数f(x)一阶展开，再进行求解。

解法分为直接解和迭代解：

马鞍面复习：

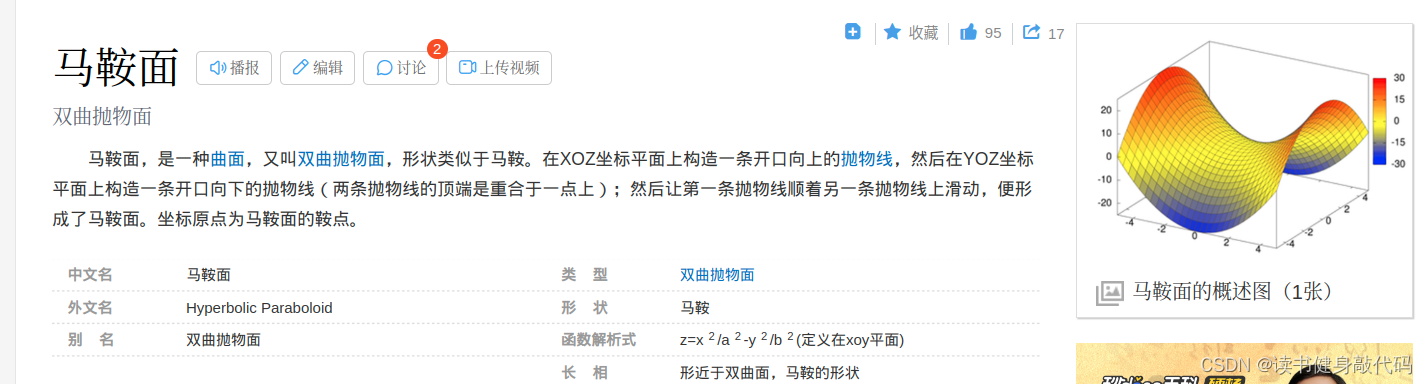
迭代下降法本质上就是在不同的点进行(二阶)泰勒展开，忽略高阶项，展开之后进行优化。

2.1 一阶法

下降法（如果方向选择为梯度反方向则就为DL中的梯度下降法，此处叫最速下降法）：
下降法主要是找步长$\alpha$和方向$d$


最速下降法：不易收敛；牛顿法：H计算量大。

阻尼法，在牛顿法基础上增加一个$\Delta x$的正则项 $\frac{1}{2}\mathbf{\mu }\mathbf{\Delta }{\mathbf{x}}^{\mathbf{T}}\mathbf{\Delta }\mathbf{x}$，使其不会太大（牛顿法和阻尼法实际上是二阶法）：

阻尼法的阻尼是加在H上的$\mu$

为方便起见，可将残差stack起来成向量（也可以写成sum of的形式，但向量可供讨论具体小f的一些性质，相应地，雅克比J和海塞H也要相应地写为向量形式）

F(x)是cost function，最简单的例子：$minF(x)=\frac{1}{2}||f(x)|{|}_2^2$

2.2 二阶法

2.2.1 Gauss-Newton

损失函数F(x)对$\Delta x$的一阶导数可记作b，也可直接写F(x)${}^{\prime }$

具体的可以看《14讲》中的引入(P131)，有系数矩阵$D$和优化半径$\mu$(也就是这里的阻尼因子)，当系数矩阵$D=I$时，才是上述的形式。

2.2.2 LM

2.2.2.1 LM阻尼因子$\mu$初值的选取方法

1. 阻尼的理解：阻尼大小代表一阶近似的占比程度，也就代表了步长更新方向的占比程度，阻尼越大，步长值越小。$\rho$很大，则说明在下降，要增大步长加快收敛，减小阻尼$\mu$
   $\rho <0$，则说明没下降，拒绝本次迭代，减小步长，增大阻尼$\mu$。
   

---

---

2. $\tau$的设定是根据经验值而来，当前x距离$x^{\ast }$较近时，取二阶近似，初值${\mu }_0$就设的小一些,乘较小的$\tau$，距离$x^{\ast }$较远时，初值就设的应该较大，保证下降的较快，取一阶近似，乘接近于1的$\tau$

这里高翔补充了一点，：广义的韦达定理保证所有的特征值${\lambda }_i$之和跟矩阵的trace是一样的。

所以这里取$max{J}^T{J}_{ii}$矩阵的对角线的最大元素是有道理的，即可以有这样的先验：$J^T{J}_{ii}$的对角线最大元素跟$J^T{J}_{ii}$特征值的最大值是在同一个数量级，所以可取对角线最大元素来近似最大特征值。

2.2.2.2 LM阻尼因子$\mu$的更新策略

定性分析，看上面的$\Delta x$的解析形式，

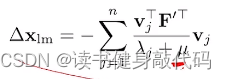
$\mu$处于分母上，增大阻尼$\mu$会减小步长（有负号不一定代表就是负值，只能整体当做正值来理解才说得通），也符合“阻尼”的直观感受：当某次$\Delta x$使得cost function增大，则应该增大阻尼使$\Delta x$变小，减小步长；反之，如果cost function在下降则应该减小阻尼$\mu$，增大步长，加快收敛速度。

上述推导说明分母一定是>0的，因为寻找的$\Delta x$会使L每次都使得L下降，但是cost function F不一定会下降（因为L是对F的二次近似，理论保证是L每次都会下降，但是实际F不一定下降），所以当$\rho <0$时表示F上升了。
当$\rho$>1时代表此时方向是正确的，则应减小$\mu$加快下降速度；如果0<$\rho$<1则代表则代表实际下降比较小，可能已经到最优值附近，应增大$\mu$减慢下降速度。

$\Delta x$越小说明近似的越好，越接近最优值。

发现了14讲关于这个$\mu$更新策略的一个错误，$\rho >\frac{3}{4}$时应该减小阻尼$\mu$，$\rho <\frac{1}{4}$时应该增大阻尼$\mu$

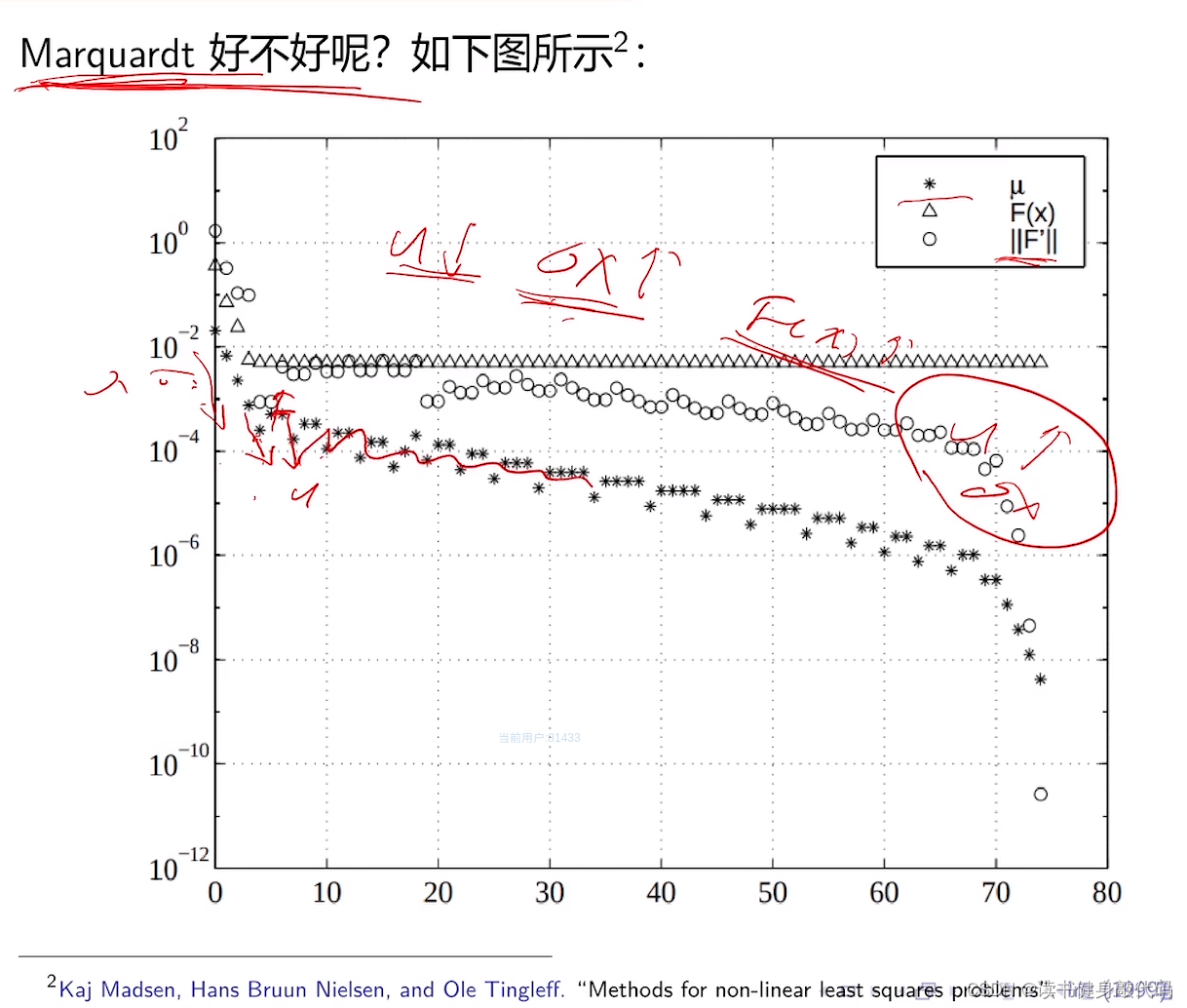
Nielsen采用了新的$\rho$的计算策略，分母直接为L，判断$\rho$的符号，当F下降时逐渐减小$\rho$，当增大时，$\rho$