什么样的程序才是好的程序?好的程序设计无外乎两点,"快"和"省"。"快"指程序执行速度快,高效,"省"指占用更小的内存空间。这两点其实就对应"时间复杂度"和"空间复杂度"的问题。那么如何分析程序的时间复杂度和空间复杂度?大O表示法。
定义
"大O表示法"表示程序的执行时间或占用空间随数据规模的增长趋势。
算法的时间复杂度通常用大O符号表述,定义为 T[n] = O(f(n))。称函数 T(n) 以 f(n) 为界或者称 T(n) 受限于 f(n)。 如果一个问题的规模是 n,解这一问题的某一算法所需要的时间为 T(n)。T(n) 称为这一算法的“时间复杂度”。当输入量n逐渐加大时,时间复杂度的极限情形称为算法的“渐近时间复杂度”。

简介
我们常用大O表示法表示时间复杂度,注意它是某一个算法的时间复杂度。大O表示只是说有上界,由定义如果 f(n)=O(n),那显然成立 f(n)=O(n^2),它给你一个上界,但并不是上确界,但人们在表示的时候一般都习惯表示前者。此外,一个问题本身也有它的复杂度,如果某个算法的复杂度到达了这个问题复杂度的下界,那就称这样的算法是最佳算法。
大O表示法可以帮助我们快速分析算法的性能优劣,也可以帮助我们分析一个算法的实用性。
图例说明
画一个 16 个格子的网格,下面分别列举几种不同的画法,并用大O表示法表示。
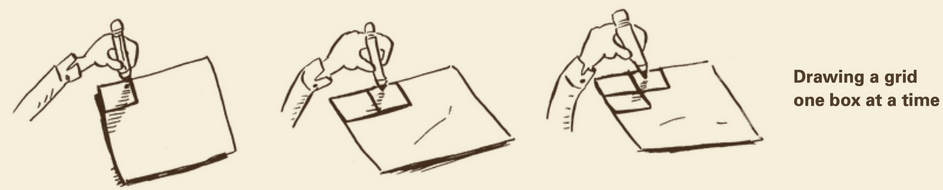
一次画一个格子
如下图所示。时间复杂度为 O(n)。
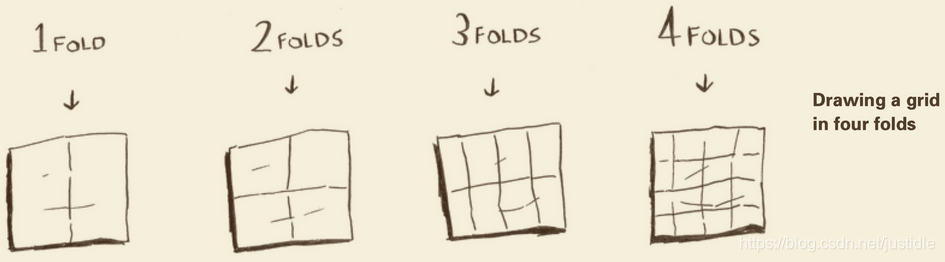
折叠纸张
折叠四次就能出现16个格子,如下图所示。时间复杂度为 O(logN)。
一些常见的大O运行时间
-
O(log n),也叫对数时间,二分查找。
-
O(n),也叫线性时间,简单查找。
-
O(n * log n),快速排序——一种速度较快的排序算法。
-
O(n²),选择排序——一种速度较慢的排序算法。
-
O(n!),旅行商问题的解决方案——一种非常慢的算法。
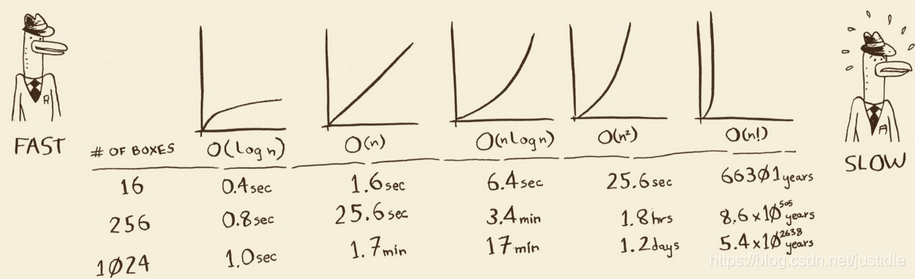
总结
-
算法的速度指的是操作数的增速,而非时间。
-
谈论算法速度说的是随着输入的增加,其运行时间将以什么样的速度增加。
-
用大O表示法表示算法的运行时间。
-
随着元素的增加,快算法比慢算法增加的速度是指数级的。比如,O(log n) 和 O(n)。
P.S.
旅行商问题就是:一个销售员,要去5个城市,他想规划一下最短距离,然后选出最短的距离。5个城市一共有120种规划方案(5!)。n个城市就有n!种规划方案。旅行商问题在计算机科学领域是无解的。
























 3126
3126

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










