Softmax函数求导

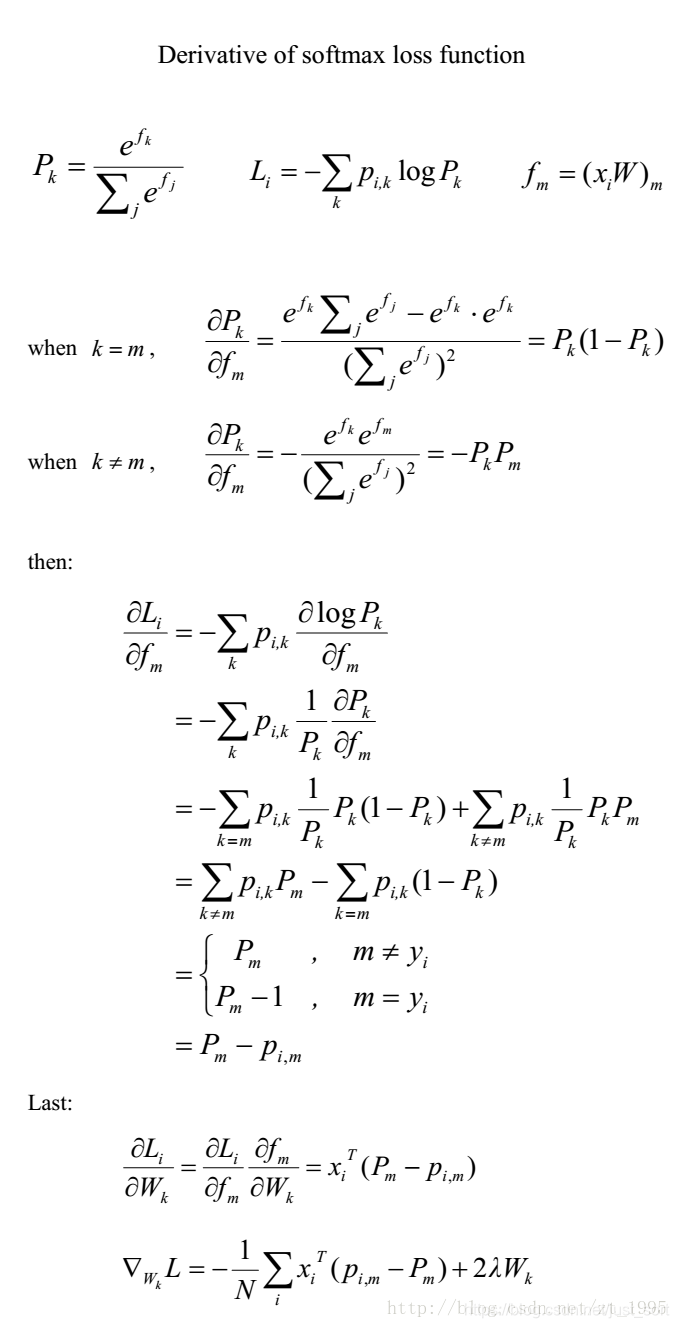
来源：https://blog.youkuaiyun.com/zt_1995/article/details/62227603

其实整个推导，上面这个图片已经介绍得十分清楚了，但是仍有很多小步骤被省略掉了，我会补上详细的softmax求导的过程：
(1)softmax函数
\quad首先再来明确一下softmax函数，一般softmax函数是用来做分类任务的输出层。softmax的形式为:
$S_i=\frac{e^{z_i}}{{\sum }_k{e}^{z_k}}$ 其中$S_i$表示的是第i个神经元的输出，接下来我们定义一个有多个输入，一个输出的神经元。神经元的输出为$z_i={\sum }_{ij}{x}_{ij}+b$，其中$w_{ij}$是第$i$个神经元的第$j$个权重,b是偏移值.$z_i$表示网络的第$i$个输出。给这个输出加上一个softmax函数，可以写成:$a_i=\frac{e^{z_i}}{{\sum }_k{e}^{z_k}}$, 其中$a_i$表示softmax函数的第i个输出值。这个过程可以用下图表示:

(2)损失函数
softmax的损失函数一般是选择交叉熵损失函数，交叉熵函数形式为$C=-{\sum }_i{y}_{i}ln{a}_i$，其中y_i表示真实的标签值
(3)需要用到的高数的求导公式

c'=0(c为常数）
(x^a)'=ax^(a-1),a为常数且a≠0
(a^x)'=a^xlna
(e^x)'=e^x
(logax)'=1/(xlna),a>0且 a≠1
(lnx)'=1/x
(sinx)'=cosx
(cosx)'=-sinx
(tanx)'=(secx)^2
(secx)'=secxtanx
(cotx)'=-(cscx)^2
(cscx)'=-csxcotx
(arcsinx)'=1/√(1-x^2)
(arccosx)'=-1/√(1-x^2)
(arctanx)'=1/(1+x^2)
(arccotx)'=-1/(1+x^2)
(shx)'=chx
(chx)'=shx
（uv)'=uv'+u'v
(u+v)'=u'+v'
(u/)'=(u'v-uv')/^2 

(3)进行推导
我们需要求的是loss对于神经元输出$z_i$的梯度，求出梯度后才可以反向传播，即是求:
$\frac{\partial C}{\partial z_i}$, 根据链式法则(也就是复合函数求导法则)$\frac{\partial C}{\partial a_j}\frac{\partial a_j}{\partial z_i}$，初学的时候这个公式理解了很久，为什么这里是$a_j$而不是$a_i$呢？这里我们回忆一下softmax的公示，分母部分包含了所有神经元的输出，所以对于所有输出非i的输出中也包含了$z_i$，所以所有的a都要参与计算，之后我们会看到计算需要分为$i=j$和$i̸=j$两种情况分别求导数。
首先来求前半部分：
$\frac{\partial C}{\partial a_j}=\frac{-{\sum }_j{y}_{i}ln{a}_j}{\partial a_j}=-{\sum }_j{y}_j\frac{1}{a_j}$,接下来求第二部分的导数，如果$i=j$，$\frac{\partial a_i}{\partial z_i}=\frac{\partial (\frac{e^{z_i}}{{\sum }_k{e}^{z_k}})}{\partial z_i}=\frac{{\sum }_k{e}^{z_k}{e}^{z_i}-(e^{z_i}{)}^2}{({\sum }_k{e}^{z_k}{)}^2}=(\frac{e_i^z}{{\sum }_k{e}^{z_k}})(1-\frac{e^{z_i}}{{\sum }_k{e}^{z_k}})=a_i(1-a_i)$，如果$i̸=j$，$\frac{\partial a_i}{\partial z_i}=\frac{\partial \frac{e^{z_j}}{{\sum }_k{e}^{z_k}}}{\partial z_i}=-e^{z_j}(\frac{1}{{\sum }_k{e}_k^z}{)}^2{e}^{z_i}=-a_i{a}_j$，接下来把上面的组合之后得到$\frac{\partial C}{\partial z_i}=(-{\sum }_j{y}_j\frac{1}{a_j})\frac{\partial a_j}{\partial z_i}=-\frac{y_i}{a_i}{a}_i(1-a_i)+{\sum }_{j̸=i}\frac{y_j}{a_j}{a}_i{a}_j=-y_i+y_i{a}_i+{\sum }_{j̸=i}{\frac{y_j}{a}}_i=-y_i+a_i{\sum }_j{y}_j$，推导完成!
(4)对于分类问题来说，我们给定的结果$y_i$最终只有一个类别是1,其他是0，因此对于分类问题，梯度等于：
$\frac{\partial C}{\partial z_i}=a_i-y_i$

最后放一份CS231N的代码实现，帮助进一步理解：

#coding=utf-8
import numpy as np

def softmax_loss_native(W, X, y, reg):
    '''
    Softmax_loss的暴力实现，利用了for循环
    输入的维度是D，有C个分类类别，并且我们在有N个例子的batch上进行操作
    输入:
    - W: 一个numpy array，形状是(D, C)，代表权重
    - X: 一个形状为(N, D)为numpy array，代表输入数据
    - y: 一个形状为(N,)的numpy array，代表类别标签
    - reg: (float)正则化参数
    f返回:
    - 一个浮点数代表Loss
    - 和W形状一样的梯度
    '''
    loss = 0.0
    dW = np.zeros_like(W) #dW代表W反向传播的梯度
    num_classes = W.shape[1]
    num_train = X.shape[0]
    for i in xrange(num_train):
        scores = X[i].dot(W)
        shift_scores = scores - max(scores) #防止数值不稳定
        loss_i = -shift_scores[y[i]] + np.log(sum(np.exp(shift_scores)))
        loss += loss_i
        for j in xrange(num_classes):
            softmax_output = np.exp(shift_scores[j]) / sum(np.exp(shift_scores))
            if j == y[i]:
                dW[:, j] += (-1 + softmax_output) * X[i]
            else:
                dW[:, j] += softmax_output * X[i]
    loss /= num_train
    loss += 0.5 * reg * np.sum(W * W)
    dW = dW / num_train + reg * W
    return loss, dW

def softmax_loss_vectorized(W, X, y, reg):
    loss = 0.0
    dW = np.zeros_like(W)
    num_class = W.shape[1]
    num_train = X.shape[0]
    scores = X.dot(W)
    shift_scores = scores - np.max(scores, axis=1).reshape(-1, 1)
    softmax_output  = np.exp(shift_scores) / np.sum(np.exp(shift_scores), axis=1).reshape(-1, 1)
    loss = -np.sum(np.log(softmax_output[range(num_train), list(y)]))
    loss /= num_train
    loss += 0.5 * reg * np.sum(W * W)
    dS = softmax_output.copy()
    dS[range(num_train), list(y)] += -1
    dW = (x.T).dot(dS)
    dW = dW/num_train + reg*W
    return loss, dW