参考:https://blog.youkuaiyun.com/James_Ray_Murphy/article/details/79163705
离散余弦变换的特征是将物体信息能量汇聚到低频成分,高频成分接近0,因此被用于语音和图像处理领域。
在图像压缩存储中,可以将原始图像进行二维离散余弦变换,然后存储含有信息的低频部分的数据。在图像还原过程中,通过这些携带信息的低频数据就可以还原原始大小的图像。
# -*- coding: -utf-8 -*-
import cv2
import numpy as np
import matplotlib.pyplot as plt
img = cv2.imread('d:/bgs.jpg', 0) # 读取图片,
img1 = img.astype('float') # 将uint8转化为float类型
img_dct = cv2.dct(img1) # 进行离散余弦变换
img_dct_log = np.log(abs(img_dct)) # 进行log处理
img_recor = cv2.idct(img_dct) # 进行离散余弦反变换
print(img_dct.shape)
zip_len=300
# 图片压缩,只保留100*100的数据
recor_temp = img_dct[0:zip_len, 0:zip_len]
recor_temp2 = np.zeros(img.shape)
recor_temp2[0:zip_len, 0:zip_len] = recor_temp
# 压缩图片恢复
img_recor1 = cv2.idct(recor_temp2)
# 显示
plt.subplot(221)
plt.imshow(img)
plt.title('original')
plt.subplot(222)
plt.imshow(img_dct_log)
plt.title('dct transformed')
plt.subplot(223)
plt.imshow(img_recor)
plt.title('idct transformed')
plt.subplot(224)
plt.imshow(img_recor1)
plt.title('idct transformed2')
plt.show()
效果图如下:
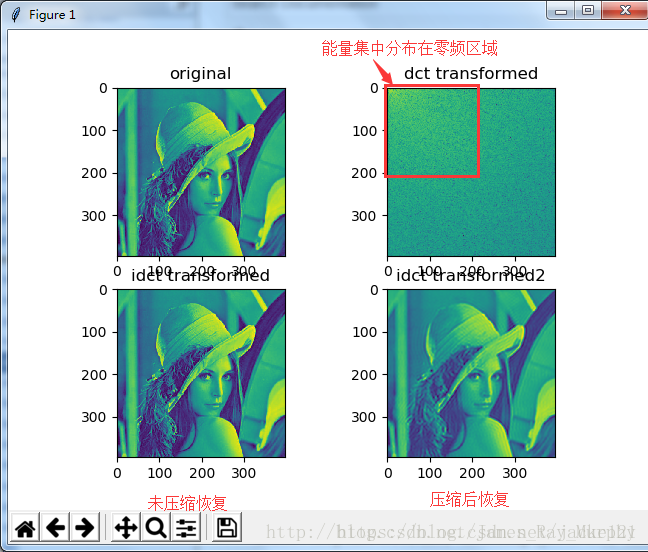








 本文介绍了Python中使用二维离散余弦变换(DCT)进行图像压缩的应用。DCT特性使图像大部分能量集中在低频部分,适合于语音和图像处理。在图像压缩中,仅保存DCT后的低频系数,还原时能重构原始图像。
本文介绍了Python中使用二维离散余弦变换(DCT)进行图像压缩的应用。DCT特性使图像大部分能量集中在低频部分,适合于语音和图像处理。在图像压缩中,仅保存DCT后的低频系数,还原时能重构原始图像。
















 1251
1251

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








