DBSCAN——非凸数据集聚类

最新推荐文章于 2025-10-02 09:14:26 发布

原创最新推荐文章于 2025-10-02 09:14:26 发布 · 1.3w 阅读

28 ·

CC 4.0 BY-SA版权

我们不生产知识，我们只是互联网的搬运工

文章标签：

#DBSCAN #聚类 #python #机器学习

编程语言同时被 2 个专栏收录

240 篇文章

订阅专栏

机器学习

136 篇文章

订阅专栏

本文通过实例展示了DBSCAN算法在非凸数据分布上的应用，对比K-Means算法，DBSCAN能更准确地识别非凸区域，适用于复杂形状的聚类分析。通过调整参数eps和min_samples，可以有效区分不同密度的簇和噪声点。

K-Means 本质上是将样本空间划分成 k 个 Voronoi 区域，决定了划分结果的 k 个簇一定是凸集，因而该方法对非凸区域的鉴别效果非常不好。
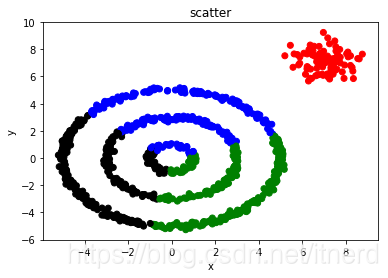
在这里插入图片描述
下面使用 DBSCAN 对上面非凸分布的数据聚类。
本例中 DBSCAN 选择的参数为：eps=0.5, min_samples=5
即要求一个团簇内点（非边界、非噪声点）在半径为 eps 的范围内至少有 min_sample 个点，边界点至少在满足上述条件一个内点的 eps 范围内，其余为噪声点。


import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import DBSCAN

def show_scatter(data,colors):
    cm = plt.cm.get_cmap('Spectral')
    x,y = data.T
    plt.scatter(x,y,c=colors,cmap=cm)
    plt.axis()
    plt.xlabel("x")
    plt.ylabel("y")

db = DBSCAN(eps=0.5, min_samples=5).fit(data)

labels = set(db.labels_)
n_clusters = len(labels) - (1 if -1 in labels else 0)
noise_mask = (db.labels_ == -1)
colors = [plt.cm.Spectral(each)
          for each in np.linspace(0, 1, len(labels))]

plt.title('Estimated number of clusters: %d' % n_clusters)
show_scatter(data[~noise_mask],db.labels_[~noise_mask])
show_scatter(data[noise_mask],'k')
plt.show()

在这里插入图片描述
图中的黑点为 DBSCAN 算法得出的噪声点。

生成上图数据的函数如下：

def gen_ring(r, var, num):
    r_array = np.random.normal(r,var,num)
    t_array = [ np.random.random()*2*np.math.pi for i in range(num)]
    data = [[r_array[i]*np.math.cos(t_array[i]),
             r_array[i]*np.math.sin(t_array[i])] 
            for i in range(num)]
    return data

def gen_gauss(mean,cov,num):     
    return np.random.multivariate_normal(mean,cov,num)
    
def gen_clusters():
    data = gen_ring(1,0.1,100)
    data = np.append(data,gen_ring(3,0.1,300),0)
    data = np.append(data,gen_ring(5,0.1,500),0)
    mean = [7,7]
    cov = [[0.5,0],[0,0.5]]
    data = np.append(data,gen_gauss(mean,cov,100),0)
    return np.round(data,4)