最优奇异值硬阈值 SVHD

原文地址：http://www.pyrunner.com/weblog/2016/08/01/optimal-svht/
本文地址：https://goodgoodstudy.blog.youkuaiyun.com/article/details/111905047

降维是许多基于 SVD 的算法中最常见的任务。通过 SVD 可以将高维、有噪声的数据集简化为低维干净的数据集。在理想情况下，专家将根据自己的判断进行降阶，但是在需要自动化的算法中没有专家参与。本文介绍一种自动化降维的算法。

一个 $m\times n$ 数据矩阵 $D$ 的 SVD 如下所示：
$$D=U\Sigma V^{\ast }$$
对数据矩阵进行 SVD ​​处理后，第一步就是快速查看 $\Sigma$ 中的奇异值，估计一下截断阶数 $r$ 的大小。有很多技术可以自动确定截断阶数，其中一种是由 Gavish 和 Donoho (2014)¹² 提出的最优奇异值硬阈值技术（Optimal Singular Value Hard Threshold）

---

SVHT

首先，建立一个数据矩阵，该矩阵包含一些结构和噪声。

选择纵轴代表空间 $x$，选择横轴代表时间 $t$。

import matplotlib.pyplot as plt
from numpy import dot, diag, exp, real, sin, cosh, tanh
from scipy.linalg import svd, svdvals

# define time and space domains
x = np.linspace(-10, 10, 100)
t = np.linspace(0, 20, 200)
Tm,Xm = np.meshgrid(t, x)

# create data
D = 5 * (1/cosh(Xm/2)) * tanh(Xm/2) * exp((1.5j)*Tm) # primary mode
D += 0.5 * sin(2 * Xm) * exp(2j * Tm)                # secondary mode
D += 0.5 * np.random.randn(*Xm.shape)                # noise

#plot
plt.matshow(np.real(D))
plt.yticks([])
plt.xticks([])
plt.ylabel('x')
plt.xlabel('t')

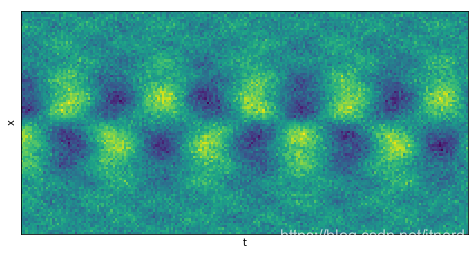
数据包含两种模式和少量正态分布 $\mathbf{N}(0,{\sigma }^2)$ 的噪声，$\sigma =0.5$

在绘制 D 的奇异值时，可以看到两个大的、分隔良好的奇异值，其余的则小得多，并且逐渐趋近于零。因此截断阶数应为 $r=2$

OSVHT 算法 将告诉我们大约在哪里截断奇异值，即确定最优截断阶数 ${\tau }^{\ast }$ 以保留数据的重要成分。

${\tau }^{\ast }$ 的计算一般分两种情况：噪声水平 $\sigma$ 已知或未知。

噪声水平未知的情况

对于未知的σ，可以用
$${\tau }^{\ast }=\omega (\beta )\cdot y_{med}$$
其中 $\beta =\frac{m}{n}$，$m,n$为数据矩阵的位数且 $m\le n$，$y_{med}$ 是 D的奇异值的中位数，而 $\omega (\beta )$可以近似为
$$\omega (\beta )\simeq 0.56{\beta }^3-0.95{\beta }^2+1.82\beta +1.43$$
注意，精确计算$\omega$也是可以的，但要求用数值方法计算 Marchenko-Pastur分布的中位数 ${\mu }_{\beta }$³。Gavish 和 Donoho 提供了MATLAB源代码补充，演示了如何进行此操作²。一旦有了${\mu }_{\beta }$，则精确的$\omega$ 由下式给出：
$$\omega (\beta )=\frac{{\lambda }^{\ast }(\beta )}{\sqrt{{\mu }_{\beta }}}$$
其中 ${\lambda }^{\ast }(\beta )$ 稍后解释

def omega_approx(beta):
    """Return an approximate omega value for given beta. Equation (5) from Gavish 2014."""
    return 0.56 * beta**3 - 0.95 * beta**2 + 1.82 * beta + 1.43

# do SVD and find tau star hat
U,sv,Vh = svd(D, False)
beta = min(D.shape) / max(D.shape)
tau = np.median(sv) * omega_approx(beta)

#plot
plt.plot(sv, 'b*', label='sigular values')
plt.plot([0,len(sv-1)],[tau,tau], 'r--', label=r'$\tau^*$')
plt.legend()

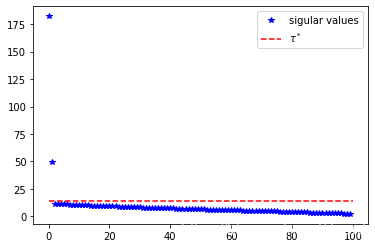
在上面的奇异值图中，红线表示 ${\tau }^{\ast }$。

现在我们有了最佳的 SVHT，可以截断 SVD 并重建数据。重建后的数据相当于经过了降噪！

sv2 = sv.copy()
sv2[sv < tau] = 0
D2 = dot(dot(U, diag(sv2)), Vh)

#plot
plt.matshow(np.real(D2))
plt.yticks([])
plt.xticks([])
plt.ylabel('x')
plt.xlabel('t')

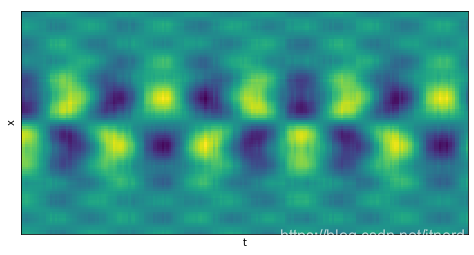
噪声水平已知的情况

当 $\sigma$ 已知时，公式略有不同：
$${\tau }^{\ast }={\lambda }^{\ast }(\beta )\cdot \sqrt{n}\cdot \sigma$$
其中 $n$ 是数据矩阵维度的较大者，
$${\lambda }^{\ast }(\beta )=\sqrt{2(\beta +1)+\frac{8\beta }{\beta +1+\sqrt{{\beta }^2+14\beta +1}}}$$

以下代码假定噪声水平 $\sigma =0.5$

def lambda_star(beta):
    """Return lambda star for given beta. Equation (11) from Gavish 2014."""
    return np.sqrt(2 * (beta + 1) + (8 * beta) / 
                   (beta + 1 + np.sqrt(beta**2 + 14 * beta + 1)))

# find tau star
tau = lambda_star(beta) * np.sqrt(max(D.shape)) * 0.5

plt.plot(sv, 'b*', label='sigular values')
plt.plot([0,len(sv-1)],[tau,tau], 'r-', label=r'$\tau^*$')
plt.legend()

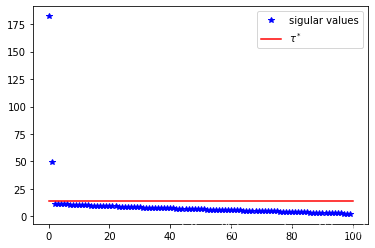
综上所述

把两种情况的代码合并

def svht(X, sigma=None, sv=None):
    """Return the optimal singular value hard threshold (SVHT) value.
    `X` is any m-by-n matrix. `sigma` is the standard deviation of the 
    noise, if known. Optionally supply the vector of singular values `sv`
    for the matrix (only necessary when `sigma` is unknown). If `sigma`
    is unknown and `sv` is not supplied, then the method automatically
    computes the singular values."""

    try:
        m,n = sorted(X.shape) # ensures m <= n
    except:
        raise ValueError('invalid input matrix')
    beta = m / n # ratio between 0 and 1
    if sigma is None: # sigma unknown
        if sv is None:
            sv = svdvals(X)
        sv = np.squeeze(sv)
        if sv.ndim != 1:
            raise ValueError('vector of singular values must be 1-dimensional')
        return np.median(sv) * omega_approx(beta)
    else: # sigma known
        return lambda_star(beta) * np.sqrt(n) * sigma

# find tau star hat when sigma is unknown
tau = svht(D, sv=sv)
print(tau)

# find tau star when sigma is known
tau = svht(D, sigma=0.5)
print(tau)

例子

1. 纯噪声

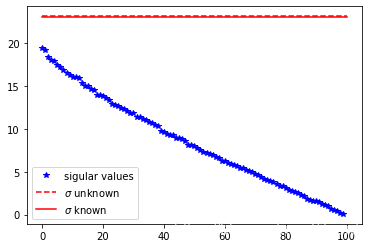
当数据矩阵是纯噪声时，算法给出的建议是把所有奇异值舍弃！！

# create matrix of random data
D = np.random.randn(100, 100)

plt.matshow(D)
plt.yticks([])
plt.xticks([])

# do SVD and find tau stars
U,sv,Vh = svd(D, False)
tau1 = svht(D, sv=sv) # sigma unknown
tau2 = svht(D, sigma=1) # sigma known
plt.plot(sv, 'b*', label='sigular values')
plt.plot([0,len(sv-1)],[tau1,tau1], 'r--', label=r'$\sigma$ unknown')
plt.plot([0,len(sv-1)],[tau2,tau2], 'r-', label=r'$\sigma$ known')
plt.legend()

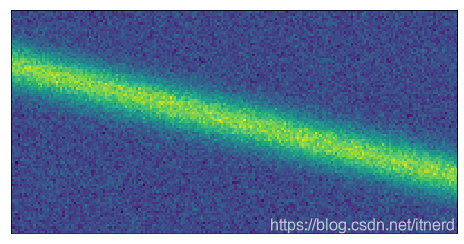
2. 平移不变性（？）

# create data with a single mode traveling both spatially and in time
D = exp(-np.power((Xm-(Tm/2)+5)/2, 2))
D += 0.1 * np.random.randn(*Xm.shape) # noise
plt.matshow(D)
plt.yticks([])
plt.xticks([])

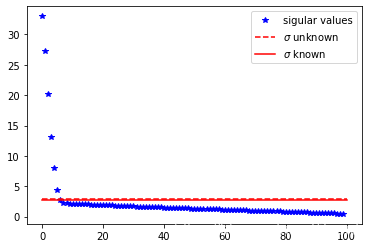
# do SVD and find tau stars
U,sv,Vh = svd(D, False)
tau1 = svht(D, sv=sv) # sigma unknown
tau2 = svht(D, sigma=0.1) # sigma known

# plot
plt.figure()
plt.plot(sv, 'b*', label='sigular values')
plt.plot([0,len(sv-1)],[tau1,tau1], 'r--', label=r'$\sigma$ unknown')
plt.plot([0,len(sv-1)],[tau2,tau2], 'r-', label=r'$\sigma$ known')
plt.legend()

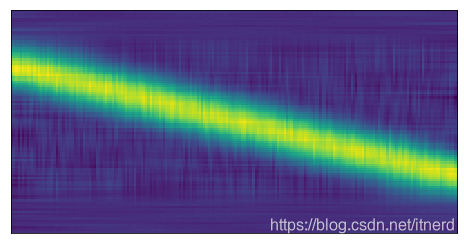
sv2 = sv.copy()
sv2[sv < tau1] = 0
D2 = dot(dot(U, diag(sv2)), Vh)
plt.matshow(D2)
plt.yticks([])
plt.xticks([])

参考文献

---

1. Gavish, Matan, and David L. Donoho. “The optimal hard threshold for singular values is.” IEEE Transactions on Information Theory 60.8 (2014): 5040-5053. ↩︎

2. Gavish, Matan, and David L. Donoho. Code supplement to “The optimal hard threshold for singular values is.” [Online]. Available: http://purl.stanford.edu/vg705qn9070 ↩︎ ↩︎

3. Wikipedia contributors. “Marchenko–Pastur distribution.” Wikipedia, The Free Encyclopedia. Wikipedia, The Free Encyclopedia, 29 May. 2016. Web. 31 Jul. 2016. ↩︎