针状手术腕部设计与实现

用于手术器械的针状手腕的设计、制造与测试

1 引言

随着外科器械的尺寸不断缩小，微创手术正持续被外科医生和工程师重新定义。器械越小，带来的好处越多，例如减少瘢痕和患者疼痛。针状器械甚至已被用于实施近乎无瘢痕的手术[1]，并且在儿科人群中应用也展现出令人兴奋的前景[2]。然而，随着这些器械直径的减小，制造灵巧性高的外科器械变得愈发困难。因此，现有的针状器械灵巧性有限，自由度数量也较少，限制了其潜在的应用价值。本文提出的腕部设计目标是为针状手术工具提供更多的自由度和更高的灵巧性。所增加的灵巧性和自由度可以增强现有用于微腹腔镜手术[3]、视网膜手术[4]和妇科手术[5]的针状器械，同时还能在解剖结构中导航尖锐拐角，例如在颅底[6,7]、中耳[8]和踝关节[9]中遇到的情况。

文献中已提出多种不同的腕部设计，包括基于传统机械连杆的设计，如球形关节[10]、万向节[11]、钢丝和滑轮[12–14]、丝杠[15,16]、并联串联机构[17]以及柔性铰链[18,19]。这些设计的尺寸范围从2.4到15毫米。尽管这些设计在一定程度上都可以缩小尺寸，但连续体结构通常比机械连杆更容易实现微型化。

已设计出多种形式的连续体腕部和灵巧结构，包括缆环设计[20]、滚动变中性线机构[21]、互锁纤维设计[22,23]、柔性多骨架设计[24]、柔顺滚动接触设计[25]以及柔性管状镍钛合金结构[26]等。目前正针对经鼻颅底手术进行研究的一种有前景的设计是参考文献[27]中提出的多驱动机构，该机构利用多根钢丝布线来构建单一可操控装置。有关现有可弯曲外科器械中所用关节的全面综述，请参见参考文献[28]。总体而言，组件更少的设计表现出更好的可扩展性，因此通过选择性去除圆柱基材材料以形成柔性元件的设计具有较大吸引力。

多个研究团队已对在镍钛合金管上制造柔性弯曲区域进行了研究。库策等人开发了一种用于关节镜手术的6毫米器械，该器械采用矩形对称切口[29]。魏等人在镍钛合金管上采用三角形切口来制造类似的操作器[30]。菲舍尔等人开发了一种用于内窥镜摄像头导向的10毫米器械[31]。多个研究团队开展了各种有限元分析，以辅助镍钛合金管中柔性弯曲区域的设计[32,33]。芳贺等人和贝尔等人均制造了带有可弯曲镍钛合金头端的导管[34][35]，而柳等人则利用加工镍钛合金管制造出一种可操控针尖[36]。

在本研究中，我们研制了一种用于针状手术工具的微型腕部，该腕部通过在镍钛合金管上加工非对称矩形切口制成，形成一个由单根肌腱驱动的柔顺弯曲区域。该腕部可装配各种手术末端执行器，用于在狭小空间内输送治疗（见图1）。我们的腕部设计最接近于参考文献[34–36]中的导管和针式设计，但其工作原理更为简单，并能实现更紧密的弯曲。我们的腕部结构易于制造，无需采用复杂的弹簧切口设计，也不依赖参考文献[34]中主动导管所使用的液压驱动。该腕部尺寸足够小，可用于针状器械，且不需要像参考文献[35]中主动导管设计所必需的镍钛合金复位弹簧。与参考文献[36]中的主动针设计相比，我们的腕部能在更小的曲率半径上实现更大的偏转角度。该腕部采用单根肌腱驱动，可通过低成本的制造方法进行原型制作。该设计具有可扩展性，能够方便地集成到针状手术工具中。

本工作的贡献包括验证了非对称切口腕部的运动学和静力学模型、一种低成本制造工艺、实现腕部尖端优先弯曲的设计方法，以及对腕部疲劳寿命和可扩展性的实验测试。本文部分结果的初步版本见于参考文献[37]。在参考文献[37]中推导了运动学和静力学模型，并提出了一种腕部原型。本归档论文的新增与改进内容包括一种新的肌腱连接方法、将腕部缩小至0.5 mm以下的物理演示，以及将该腕部集成到用于经鼻颅底手术的针状装置中。

2 设计概念

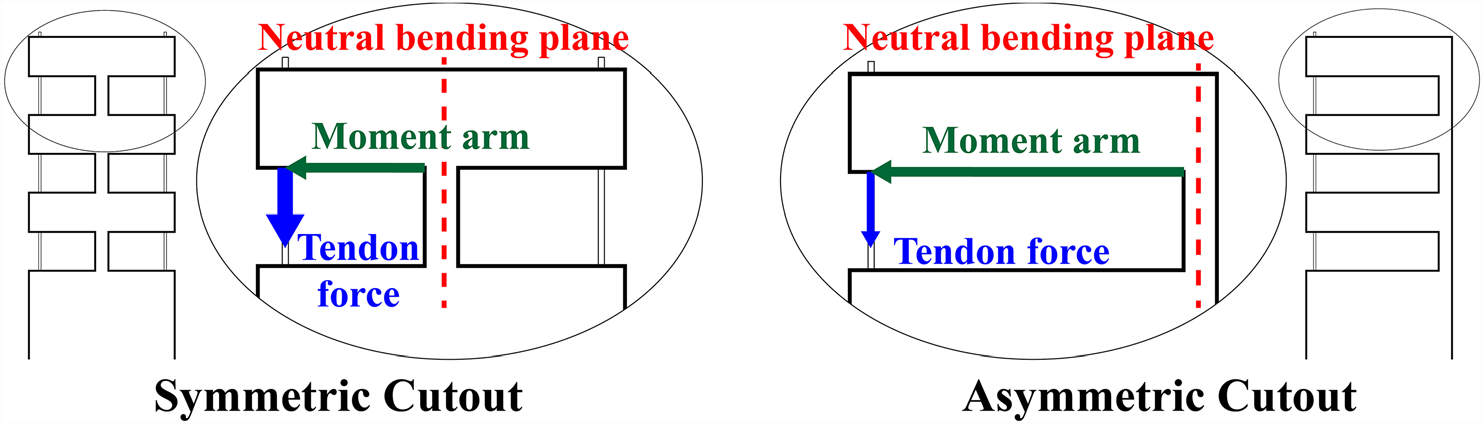
腕部由在镍钛合金管上加工的一系列非对称切口构成（见图1）。这些切口选择性地改变管尖沿长度方向的弯曲刚度，并通过单根肌腱实现腕部的驱动。尽管对称切口已在多种装置中得到研究[29,31,32]，但非对称切口几何结构相较于对称切口具有多项优势（见图2）。采用非对称切口可在肌腱与中性弯曲面之间形成更长的力臂，从而降低驱动所需的力。此外，非对称设计仅需一根肌腱即可驱动，相比对称设计简化了肌腱布线，并提升了设计的可扩展性。最后，非对称设计的中性弯曲面存在偏移，使得腕部中心线处的曲率半径更小。尽管非对称设计只能向一个方向弯曲，但只要整个装置能够旋转，这并不会成为主要问题。

我们微型腕部的另一个关键特点是易于与针状工具集成，这是通过直接在针体上加工腕部实现的。这种方法避免了使用粘合剂或其他机械紧固件将腕部固定在毫米尺度管末端的需求。其他腕部设计需要在腕部与工具轴之间建立连接（参见参考文献[15,19]等），而在毫米尺度下，这种连接最终可能存在问题，因为可用表面积通常不足以使用粘合剂，且无法获得合适的机械紧固件。

3 运动学模型

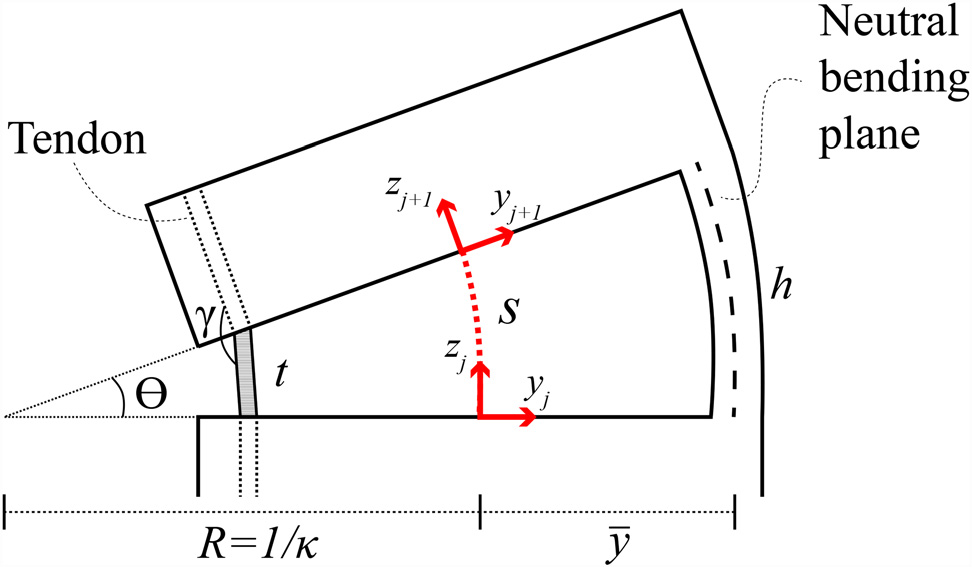
为了建立腕部的运动学模型，我们首先考虑单个切口。我们假设所有弯曲都发生在切口段，并且这些段变形为圆弧。以与参考文献相同的方式，[38]肌腱位移（执行器空间）被映射到弧形参数（构型空间），然后弧形参数被映射到任务空间。我们所求的曲率（j）和弧长（s）在图3中定义。关于下述运动学模型的完整推导，请参见参考文献[37]。

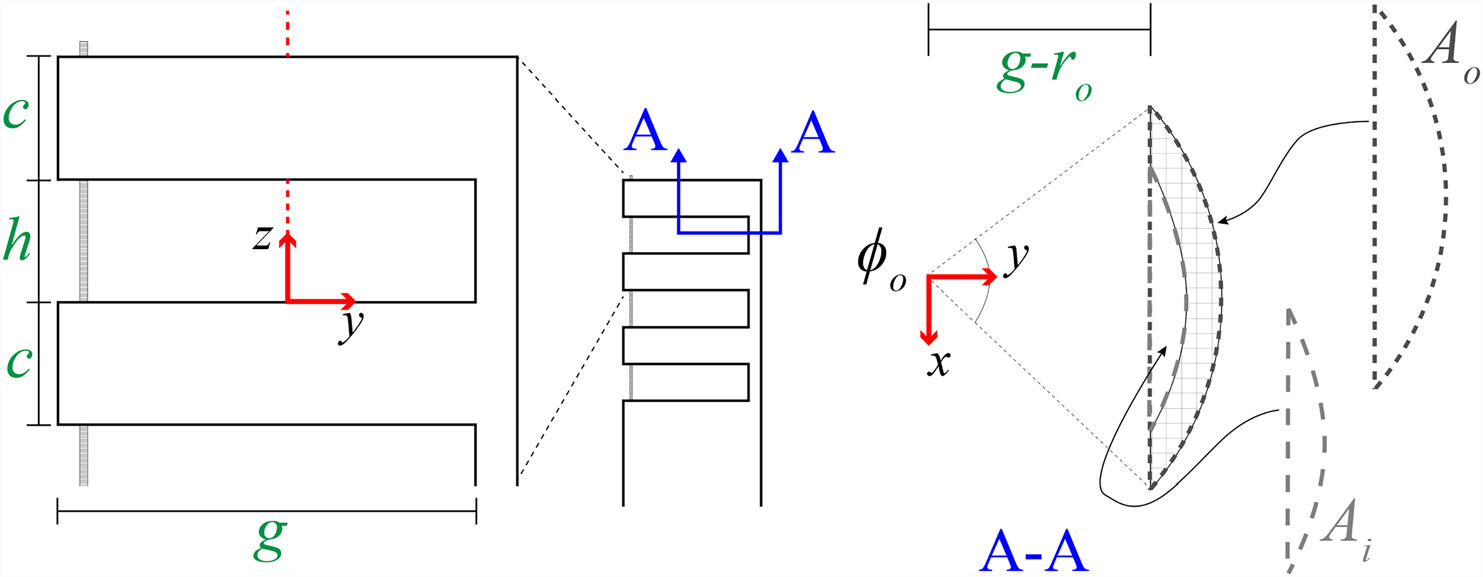
为了确定j和s，需对切口的中性弯曲面进行分析。中性弯曲面是构件中在弯曲时既不伸长也不缩短的区域。在弯曲过程中不产生纵向应变。对于我们的腕部，中性弯曲面 y假设与管的切口部分轴向截面的形心相交（见图4的A–A剖视图）。该 y的位置适用于切割深度至少等于管外半径的情况，其表达式为

$$
\bar{y} = \frac{\bar{y}_o A_o - \bar{y}_i A_i}{A_o - A_i}
$$

其中面积 $A_o$ 和 $A_i$ 在图4中定义，$\bar{y}_o$ 和 $\bar{y}_i$ 分别为它们的形心，而 $\theta_o$ 和 $\theta_i$ 为它们的中心角

$$
A_o = r_o^2 \theta_o - \frac{\sin(\theta_o)}{2}
$$

$$
A_i = r_i^2 \theta_i - \frac{\sin(\theta_i)}{2}
$$

$$
\bar{y}_o = \frac{4 r_o \sin^3 \left( \frac{1}{2} \theta_o \right)}{3 \theta_o - \sin(\theta_o)}
$$

$$
\bar{y}_i = \frac{4 r_i \sin^3 \left( \frac{1}{2} \theta_i \right)}{3 \theta_i - \sin(\theta_i)}
$$

$$
\theta_o = 2 \arccos \left( \frac{g - r_o}{r_o} \right)
$$

$$
\theta_i = 2 \arccos \left( \frac{g - r_o}{r_i} \right)
$$

利用 $\bar{y}$、弧形几何结构（见图3）以及小角度近似，现在可以求得给定肌腱位移（j）下的曲率（s）和弧长（Dl）

$$
j \approx \frac{Dl}{h (r_i + \bar{y}) - Dl \bar{y}}
$$

$$
s = h (1 + \bar{y} j)
$$

在坐标系j和j+1之间（如图3所定义）的齐次变换现在可以使用j和s来定义，如参考文献[37]所述。从基座到腕部末端的运动学变换可通过重复应用该齐次变换，并沿z_{j+1}轴进行平移，以考虑管体中不弯曲的刚性部分。每个部分的旋转角度可利用j和s求得，如下所示

$$
\theta_j(j) = \frac{h}{1 + \bar{y} j}
$$

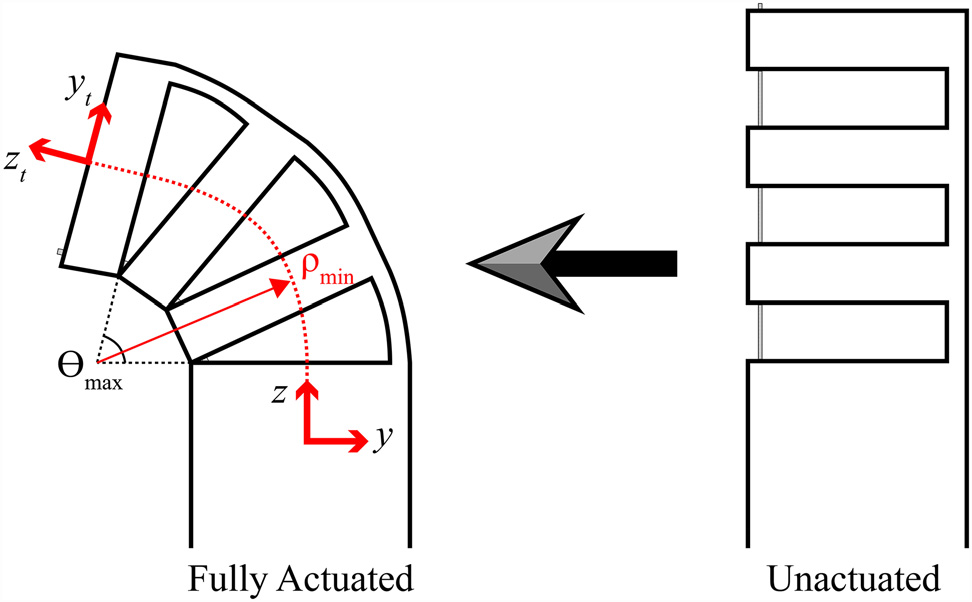
最大弯曲角度和最小曲率半径（通过完全偏转的腕部的近似圆弧；见图5）为

$$
\theta_{max} = n \frac{h}{r_o + \bar{y}}
$$

$$
\rho_{min} \approx r_o + \frac{(n - 1)c}{\theta_{max}}
$$

其中 $n$ 为切口数量。腕部运动学在第5.2节中进行了实验验证。

4 静力学模型

为了建立腕部的静力学行为模型，我们首先分析在弯曲状态下管状切口部分横截面上的应变，根据恒定曲率假设，该应变随弧长变化。

$$
\varepsilon(y, j) = \frac{j (y - \bar{y})}{1 + \bar{y} j}
$$

此处假设应变沿中性弯曲面呈线性分布，从而可以简单地计算应变能。然后可将应变能结合卡斯蒂利亚诺第一定理使用，以获得所需的驱动力。采用分段线性应力–应变曲线，本文使用了一种简化的镍钛合金材料模型，使得应力可以表示为应变的函数，如下所示：

$$
\sigma(\varepsilon) =
\begin{cases}
\sigma_{lp}, & \varepsilon < \sigma_{lp}/E \
E \varepsilon, & \sigma_{lp}/E \leq \varepsilon \leq \sigma_{up}/E \
\sigma_{up}, & \varepsilon > \sigma_{up}/E
\end{cases}
$$

其中，较低的平台应力 $\sigma_{lp}$ 对应压缩，较高的平台应力 $\sigma_{up}$ 对应拉伸，E为杨氏模量。应变能密度在此定义为应力–应变曲线下的面积 $W(\varepsilon) = \int_0^\varepsilon \sigma(\varepsilon) d\varepsilon$，因为材料变形被建模为轴向纤维的一维拉伸和压缩。腕部中存储的总应变能为 $U(j) = n \int_{V_c} W(\varepsilon(y, j)) dV$，其中体积 $V_c$ 通过剖视图A–A所示未开槽管的横截面（见图4）和开槽高度h计算得到。最后，可通过卡斯蒂利亚诺第一定理求得肌腱力F与腕部旋转角θ之间的关系。

$$
\frac{\partial U(j)}{\partial \theta} = M = F L
$$

其中 $L$ 定义了力臂长度，且 $\theta = n s j$。由于摩擦，肌腱在腕部末端施加的力将小于施加在肌腱上的驱动力。为了考虑这种摩擦损失，文献中建立了一个简单模型[37]，该模型考虑了肌腱在管的切口段单个拐角处必须经过的角度 $c$（见图3）。

肌腱经过单个拐角后施加的力定义为

$$
F = \gamma F_{tendon} = \frac{\sin(c/2) - \mu_s \cos(c/2)}{\sin(c/2) + \mu_s \cos(c/2)} F_{tendon}
$$

其中 $\mu_s$ 为静摩擦系数，$\gamma < 1$ 用于估算由于拐角引起的摩擦损耗。将公式(9)代入公式(8)，并使用 $2n$ 表示肌腱经过的拐角数量（每个切口有两个拐角），可得到肌腱力与腕部角度之间关系的方程

$$
F_{tendon} = \frac{1}{\gamma^{2n} L} \frac{\partial U(j)}{\partial \theta}
$$

静力学模型的完整推导过程参见参考文献[37]。静力学模型在第5.2节中通过实验进行了验证。

5 腕部制造与测试

对于图6中所示的原型，使用了外径（OD）为1.16 mm、内径（ID）为0.86 mm的镍钛合金管。该原型选择的切割深度为 $g = 0.965$ mm，对应的最大外层纤维应变约为10.4%。我们选择了切割高度 $h = 0.51$ mm，切口间距 $c = 0.51$ mm，以及 $n = 5$ 个切口，以实现至少90度的弯曲。这些参数选择使得腕部的最大旋转角度 $\theta_{max}$ 达到138度，最小曲率半径 $\rho_{min}$ 为1.42 mm。该腕部用于验证下文的运动学和静力学模型，并通过计算机数控（CNC）铣削工艺进行加工制造。

为了通过数控铣削制造腕部，我们首先通过在铝块中加工出一个槽来制作夹具（图7）。槽宽和深度等于镍钛合金管的外径。我们使用MicroProto系统MicroMill 2000型CNC铣床（一种小型台式数控机床，新机购买价格约为2500美元）进行端面铣削以加工该槽。镍钛合金管用氰基丙烯酸酯胶粘剂固定到夹具上。制作好夹具后，使用同一台CNC机床以及氮化铝钛涂层、双刃、碳化钨长刃方头立铣刀对镍钛合金管进行切口加工。通过此工艺制造的腕部示例如图6所示，且在图

去除切屑后的腕部表面光洁度详细视图如图8(a)所示。

我们还使用线切割放电加工（EDM）制造了与数控铣削腕部几乎相同的腕部，主要区别在于线切割EDM腕部的切口具有圆角（见图8(b)）。这些圆角是由进行切割的导线形成的，其半径由所用EDM导线的直径决定。从材料力学的基本角度来看，与方形切口设计相比，圆角应能在驱动过程中降低应力集中。然而，线切割EDM工艺产生的热量可能会在腕部材料中引入不良的材料特性。第5.3节对CNC加工的腕部和线切割EDM腕部的疲劳寿命进行了比较。

5.1 肌腱连接方法

在本研究中，腕部的驱动通过一根由NiTi合金制成的单根肌腱实现。已探索了多种将肌腱在腕部末端刚性固定的肌腱连接方法。首先，将肌腱绕过腕部末端，并穿过最远端的切口，然后返回至腕部基座[37]。还在肌腱导线末端打结（见图13）。本文所采用的方法是将肌腱固定在位于腕部末端的端盖上（见图9）。该端盖在管的外壁上有两个孔，肌腱先穿过其中一个孔，再从另一个孔回穿，最后终止于腕部末端。这种在

肌腱以及肌腱与端盖之间的摩擦可刚性固定肌腱的位置。与环状肌腱连接方法相比，该方法有助于减少摩擦对肌腱的影响，最终降低驱动腕部关节活动所需的驱动力[37]。此外，由于没有切口被导线环撑开（如参考文献[37]中所述），因此可实现腕部的完全关节活动。最后，采用单根肌腱增加了管内可用空间，以便容纳更多导线来驱动末端执行器或执行其他任务。

5.2 模型验证

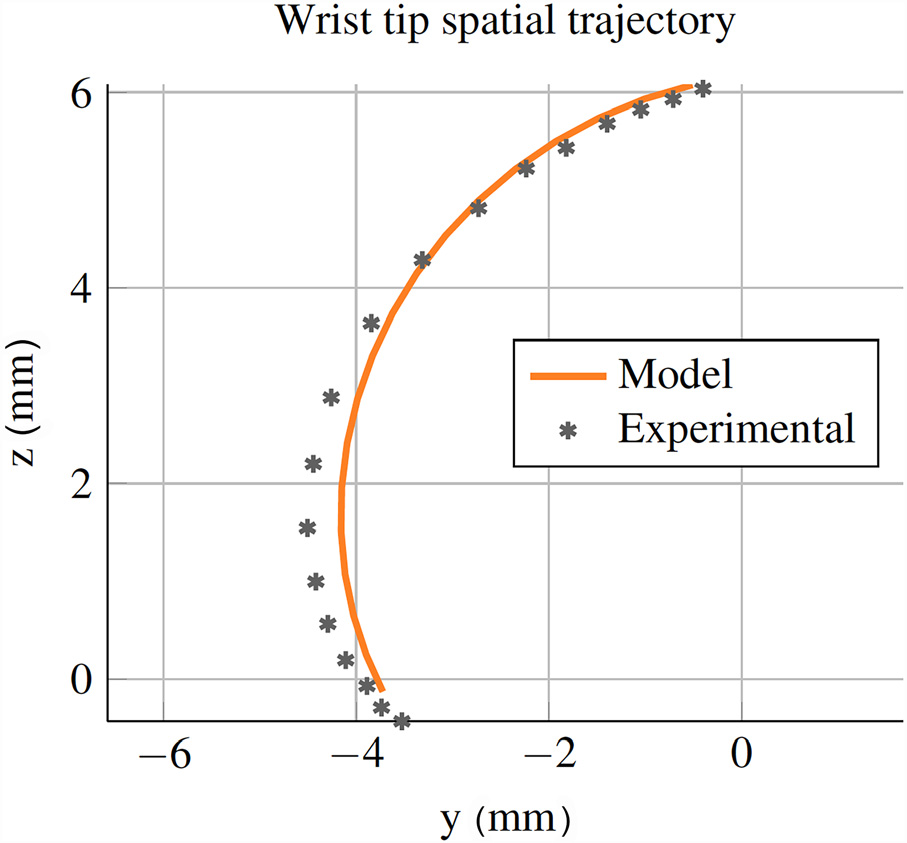
我们进行了实验，以同时探究运动学和静力学关系的准确性。使用分辨率为0.01 mm的线性滑台（Velmex A2512Q2-S2.5）来施加肌腱位移，并使用分辨率为3.125 mN的力传感器（ATI Nano 17）测量驱动腕部所需的力。力传感器安装在线性滑台上，滑台末端的夹头支架固定住腕部。一块亚克力板安装在力传感器前端，肌腱固定在该亚克力板上。肌腱在腕部末端通过端盖进行固定。通过每次增加0.2 mm的肌腱位移来使腕部逐步偏转，并利用带摄像头附件的显微镜在每个点拍摄偏转后腕部的图像（见图10）。

每幅图像均手动处理，以确定腕部的尖端位置，其与运动学模型的对比结果如图11所示。

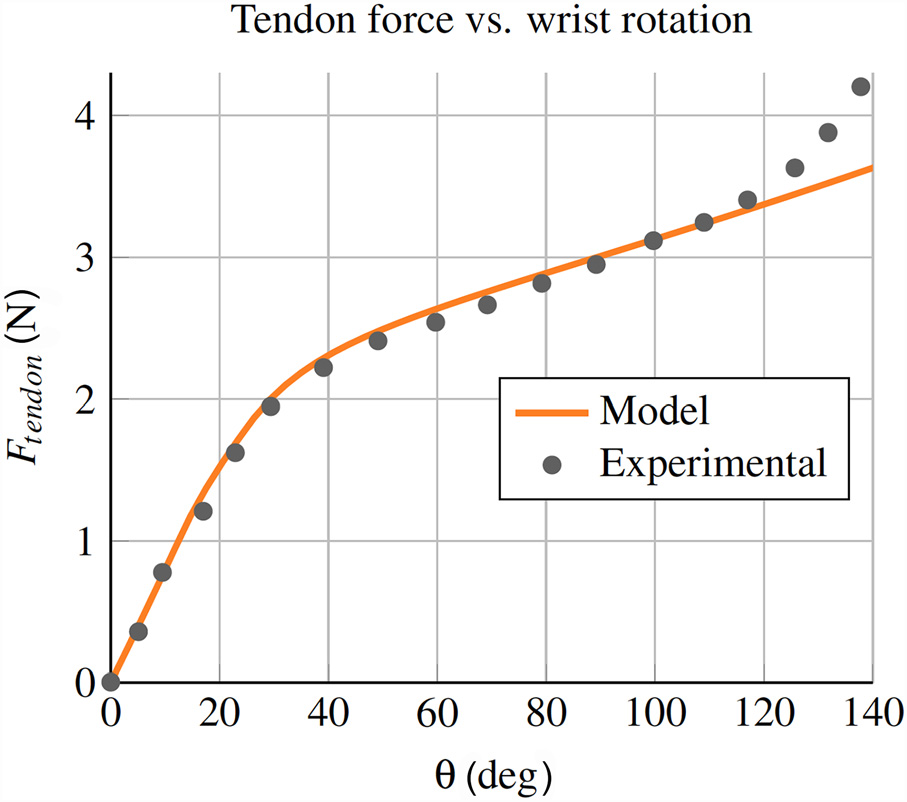
静态模型的实验对比结果如图12所示。关于材料特性，需注意镍钛合金在拉伸和压缩状态下具有非对称应力–应变关系。我们假设平台应力为 $\sigma_{lp} = -750$ MPa 和 $\sigma_{up} = 500$ MPa，杨氏模量为 $E = 60$ GPa，这些值均处于制造商和文献报道的范围内[39,40]。选取0.2的摩擦系数以考虑

肌腱经过切口的尖锐拐角时所经历的摩擦损耗。通过敏感性分析发现，静力学模型对切割深度最为敏感，切割深度变化1%会导致所需驱动力变化超过11%。相反，杨氏模量、平台应力和摩擦系数各自变化1%时，所需驱动力的变化均小于1%。

由于模型对切割深度的敏感性以及加工公差的不确定性，我们对切割深度进行了模型拟合。图12中所示模型所采用的拟合切割深度为0.988 mm，与实验数据吻合最佳。需要注意的是，该模型清晰地捕捉到了材料的超弹性非线性行为。实验数据末端的拖尾现象可能对应于已转变为马氏体的镍钛合金管部分的弹性变形[41]，而该现象未被模型捕捉到。

5.3 疲劳试验

我们进行了一项实验，以测试腕部的疲劳寿命，确保该设计在外科应用中使用时的安全性，在这些应用中，腕部可能在一次手术过程中被偏转数百次。为了测试疲劳寿命，我们构建了一个电动装置，可反复将腕部在0到90度的弯曲范围内进行驱动，同时测量肌腱的驱动力，以确定腕部何时发生断裂。数控铣削腕部在总共8397次循环后失效，而线切割EDM腕部在总共8121次循环后失效。我们还对第6.2节所述的数控铣削尖端优先弯曲腕部进行了疲劳试验，该腕部在5858次循环后断裂（请注意，该腕部的切口几何形状导致其最大关节活动角度为84度）。鉴于该腕部旨在作为一次性使用或限次使用器械（类似于达芬奇手术工具），其失效循环次数已足够充分，能够提供合理的安全系数。

6 可扩展性与尖端优先弯曲

本研究提出的腕部设计具有两个优点：一是由于机械部件数量有限且驱动方案简单，易于实现小型化；二是能够选择性地改变装置沿其长度方向的刚度。

6.1 腕部的可扩展性

通过使用单根镍钛合金管制造腕部，并采用单根肌腱驱动该腕部，理论上可将其缩小至目前可用的最小直径镍钛合金管（撰写本文时为0.178毫米[42]）。这种小型带腕部工具的一种外科应用是视网膜手术，其中所使用的工具直径通常小于0.5毫米[4]。医生通常必须在直型工具和预弯型工具之间做出选择

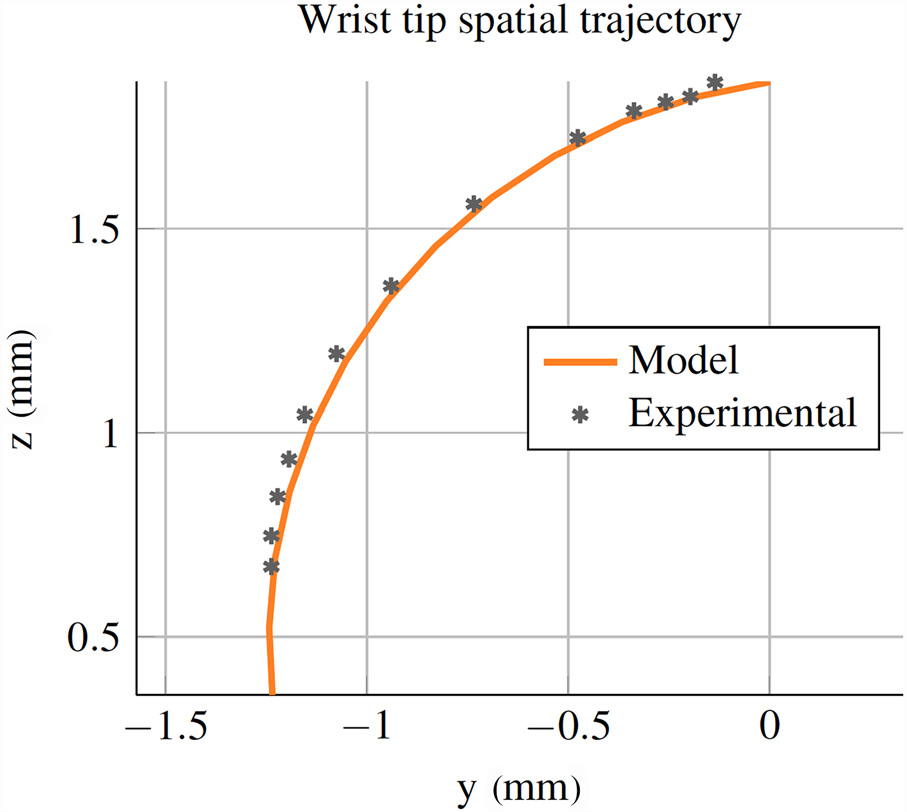
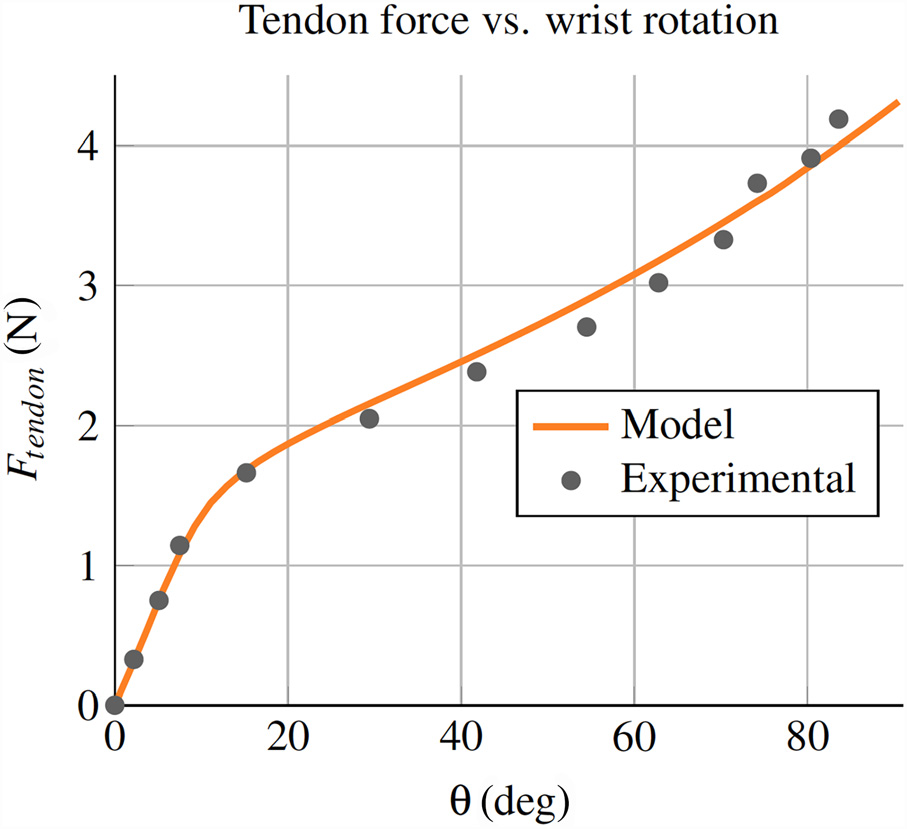
视网膜手术，因此能够选择性地偏转工具将是有益的。为了验证我们设计的可扩展性，我们使用线切割放电加工从0.46毫米外径和0.28毫米内径的镍钛合金管制造了一个微型腕部机构（见图13）。该腕部设计包含五个切口，切深为0.33毫米，切割高度为0.15毫米，切口间0.15毫米间距。我们采用第5.2节中描述的相同程序对腕部进行了实验测试，并将腕部的运动以及驱动所需力与运动学和静力学模型进行了比较。所用的镍钛合金属性与第5.2节中的相同，切深和摩擦系数通过拟合数据以达到最佳一致性。实验结果如图14和15所示，表明我们的模型可用于不同腕部几何结构。

6.2 腕部尖端优先弯曲

在空间受限的情况下，通常希望首先弯曲尖端部分，因为这样可以为每个弯曲角度实现最小的曲率半径。这种运动方式中，最远端切口首先弯曲，随后是次远端切口，依此类推，这与大多数其他肌腱驱动装置（如可操纵导管）的工作方式相反。通过调整每个切口的切割高度，我们能够在腕部实现尖端优先弯曲，使得最远端切口具有最大的切割深度，因此驱动力最小，而越靠近近端的切口其切割深度逐渐变浅。

为了实现尖端优先弯曲，我们首先选择切口数量n和切口高度h，以确定腕部的弯曲半径。然后确定最靠近近端切口的切割深度，因为我们希望该切口需要最大的驱动力并最后弯曲。最靠近近端切口的切割深度

选择近端切口，使得在完全弯曲时未切割区域承受最大允许材料应变，由 $\varepsilon_{max} = \varepsilon(r_o, 1/r_o) = (r_o - \bar{y})/(r_o + \bar{y})$ 给出。我们结合该公式与公式(1)和(2)来确定近端段的最大允许切割深度 $g_p$。然后选择最远端切口的切割深度为 $g_d = r_o + r_i$，这对应于最低允许的驱动力和材料应变。最后，通过 $g_i = (g_d - g_p)/(n - 1)$ 线性选择剩余的切割深度，其中 $g_i$ 表示从最近端切口向最远端切口方向，每个剩余切口的切割深度增量。

尖端优先弯曲16中可见，其中近端切口深度为0.965 mm，中间切口深度为0.985 mm，远端切口深度为1.005 mm。用于制造该腕部的NiTi管外径为1.16 mm，内径为0.86 mm。该腕部采用第5节所述的数控加工方法制造。

7 腕部与同心管机器人的集成

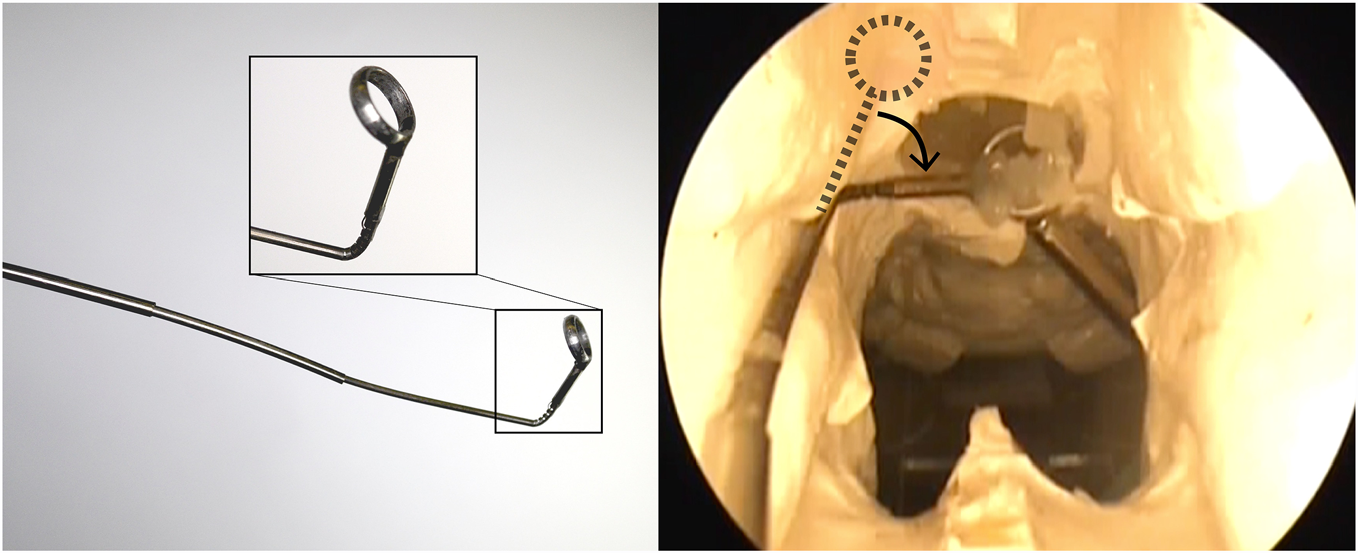
腕部最有用的特性之一是其易于集成到针状外科装置中。一种可受益于增加此类腕部的装置是同心管机器人。同心管机器人是一种针状机器人操作器，由一系列嵌套的、预弯曲的超弹性镍钛合金管组成，通常直径小于2 mm，常用于医疗应用[43]已研究将其用于前列腺切除[44]、心脏应用[45]、经鼻颅底手术[7]以及前列腺近距离放射治疗[46]。由于该腕部由镍钛合金管（与制造同心管机器人所用材料相同）制成，因此可直接在同心管机器人的最内层管上加工出腕部。这避免了需要将腕部与同心管机器人进行机械连接，从而简化了整体系统。通过使用单根肌腱驱动腕部，整个同心管机器人系统的增加的复杂性也极小。我们将该腕部集成到了参考文献[7]中提出的用于经鼻切除垂体瘤的同心管机器人中（见图17(a)）。随后，我们在相同的实验装置下，通过从颅底模型模拟体中吸除明胶来验证该腕部在此手术中的应用效果（参考文献[7]）。图17(b)显示了内窥镜视野下腕部偏转并将模拟肿瘤输送至吸除装置的过程。

8 讨论

本文所提出的腕部旨在为针状直径的手术工具提供额外的自由度和灵巧性。未来，这种腕部甚至可能实现目前使用现有刚性针状内窥镜工具无法完成的手术方法。通过将腕部直接制造在工具轴上，可轻松实现与当前刚性针状内窥镜工具的集成。建模结果能够预测装置的行为，并支持针对特定手术任务的腕部设计。该腕部结构简单、制造成本低，且设计具有可扩展性。我们还展示了在手术场景中将该腕部与同心管机器人结合使用的实例。

尽管设计简单，但仍有很大的设计空间来改变腕部性能。在本研究中，我们仅关注分析矩形切口，这种切口可利用常规微铣削技术低成本制造。采用矩形切口轮廓时，设计者可以选择切口的高度、深度以及切口之间的间距，此外还可以选择切口数量和管的外半径与内半径。通过本文中的模型和设计原则，用户可以设计出具有所需性能特性的腕部，例如最小曲率半径、最大弯曲角度和最大肌腱驱动力。

腕部最重要的两个特征是管的半径和切割深度，因为它们决定了中性弯曲面的位置，从而影响运动学、镍钛合金弯曲部分的应变以及驱动力。切割高度对腕部性能的影响不如切割深度关键，但它确实会影响弯曲半径

腕部，且必须注意不要使切割高度过大，否则会增加屈曲风险，且恒定曲率的假设将不再成立。减小切口之间的间距会减小腕部的曲率半径，因此应选择能够承受所需驱动力而不发生断裂的最小间距。非均匀切割深度的使用也会影响腕部的性能，如第6.2节所示，该能力在某些解剖场景或任务中可能具有实用价值。尽管在尖端优先弯曲设计中无法完全避免近端段的部分驱动，但第6.2节中描述的尖端优先弯曲方法可为腕部的尖端优先弯曲提供良好的近似。

模型中一个可能的误差来源是公式(6)中隐含的假设，即横截面在弯曲过程中不发生变形，这是梁弯曲分析中的常见假设。然而，由于腕部最终将由医生在直接视觉反馈下进行控制，因此这些未被捕捉到的影响可以通过人在回路中轻松校正。这一点同样适用于运动学模型与实验数据之间的任何差异。此外，实验中在极端旋转角度下的驱动力高于模型预测值，这为安全起见允许设置一个简单的最大力限制。

疲劳试验中的一个有趣观察结果是，数控加工腕部的失效循环次数比线切割EDM腕部更多。考虑到线切割EDM切口具有圆角，人们可能会预期这些圆角能够改善腕部的疲劳寿命，但此处的结果恰恰相反。进一步的疲劳试验有助于研究这两种制造方法在失效循环次数上的差异。还值得注意的是，摩擦系数这一未知参数是为了使模型与实验数据相吻合而选定的，它取决于表面光洁度和几何结构等因素。未来的研究可以探讨不同制造方法之间的其他差异，包括线切割放电加工制造是否会向镍钛合金管引入更多热量，从而改变镍钛合金的材料特性并影响腕部性能。此外，仍存在许多其他值得研究的方向，例如针对特定解剖任务的最优腕部设计，以及采用非矩形切口[36]以提升腕部性能。

9 结论

随着外科医生通过使用更小的工具不断降低手术的侵入性，为这些针状内窥镜器械的尖端提供灵活性成为迫切需求。在本研究中，我们提出了一种针状尺寸的肌腱驱动腕部，其制造简单，并可在较小的曲率半径下实现弯曲，非常适合针状内窥镜器械常需使用的狭小解剖空间。本文还提出了一种建模框架针对该腕部，使用在台式数控机床上自主制造的原型腕部对运动学与静态模型进行了验证。文中提出了简单的腕部驱动方法，并证明了该腕部设计和模型具有可扩展性。通过采用非均匀切口实现了在狭小空间中理想的尖端优先弯曲特性，并在解剖模型中展示了针状腕部的实用性。本文提出的腕部设计未来可能为外科医生提供在现有刚性工具无法使用的狭小解剖空间中进行操作所需的灵巧性，从而降低侵入性，并有望开启令人期待的新手术方法。