leetcode 797所有可能的路径

797.所有可能的路径
这个是一个典型的求路径的题(图论),也是递归方法/层序方法的实际应用,也就是我们常说的DFS和BFS在实际问题中的应用
给你一个有 n 个节点的 有向无环图（DAG），请你找出从节点 0 到节点 n-1 的所有路径并输出（不要求按特定顺序）

graph[i] 是一个从节点 i 可以访问的所有节点的列表（即从节点 i 到节点 graph[i][j]存在一条有向边）。

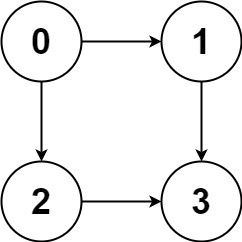
输入：graph = [[1,2],[3],[3],[]]
输出：[[0,1,3],[0,2,3]]
解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

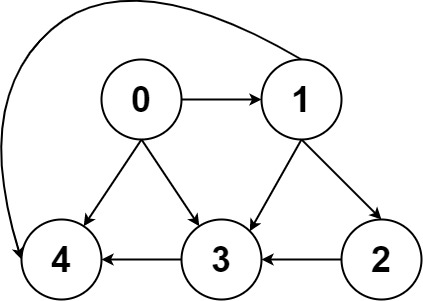
输入：graph = [[4,3,1],[3,2,4],[3],[4],[]]
输出：[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

有向无权图dfs搜索过程.需要用到回溯

class Solution:
    def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:
    		result = []
    		current_path = []
    		target = len(graph) - 1 # 一定要先定好目标是什么
    		def dfs(current_node, current_path):
    			if (current_node == target):
    				result.append(current_path)
    				return
    			for neighbor in graph[current_node]:
    				current_path.append(neighbor)
    				dfs(neighbor, current_path)
    				current_path.pop()
    		
			dfs(0, [0])
			return result

咋一看好像没啥问题,但是其实答案永远都是输出0,这是为什么呢,因为对于result.append(curren_path)来说,存入的是current_path的引用,此时如果current_path变化,result也就会跟着变化,所以需要注意,我们再使用append装数组的时候,需要通过copy来存储副本:

result.append(current_path.copy()]

最终的解答为

class Solution:
    def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:
    		result = []
    		current_path = []
    		target = len(graph) - 1 # 一定要先定好目标是什么
    		def dfs(current_node, current_path):
    			if (current_node == target):
    				result.append(current_path.copy)
    				return
    			for neighbor in graph[current_node]:
    				current_path.append(neighbor)
    				dfs(neighbor, current_path)
    				current_path.pop()
    		
			dfs(0, [0])
			return result

本质上就是一个二维数组的递归遍历,其实也是DFS的方法.还有一中更加简单的写法

class Solution:
    def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:
    	self.result = []
    	self.path = []
    	self.target = len(graph)-1

		self.traverse(graph, 0)
		return self.result

	def traverse(self, graph, current_node):
		# 前序
		self.path.append(current_node)
		if current_node == self.target:
			self.result.append(self.path.copy())
			self.path.pop()
			return
		
		for neighbor in graph[current_node]:
			self.traverse(graph, neighbor)
		# 后序
		self.path.pop() # 移除节点s

如果要用BFS,那么可以这样实现

class Solution:
    def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:
        result = []
        target = len(graph) - 1
        current_path = [0]
        q = deque()
        q.append(current_path)

        while q:
            last_node = current_path[-1]
            current_path = q.popleft()
            if current_path[-1] == target:
                result.append(current_path.copy())
                continue
            for neighbor in graph[last_node]:
                new_path = current_path.copy()
                new_path.append(neighbor)
                q.append(new_path)

        return result
						

这里唯一的注意点就是bfs找路,遍历的过程要用deque记录的是路径而不是节点,所以deque.popleft提取的是一条一条的路,直到这条路满足到达终点的硬性条件.