最小二乘融合gps与lidar定位的结果

通过最小二乘法来对两条轨迹进行拟合，然后输出对应的gps转map的外参：

import rosbag
import numpy as np
import matplotlib.pyplot as plt
from scipy.spatial import KDTree
from scipy.linalg import svd
import datetime


def latlon_to_utm(latitudes, longitudes):
    """
    将经纬度坐标转换为UTM坐标
    """
    sa = 6378137.000000
    sb = 6356752.314245
    e2 = (sa ** 2 - sb ** 2) / sa ** 2
    e = np.sqrt(e2)
    lat_rad = np.deg2rad(latitudes)
    lon_rad = np.deg2rad(longitudes)
    zone = np.floor((np.rad2deg(lon_rad) + 180) / 6) + 1
    lambda0 = ((zone - 1) * 6 - 180 + 3) * np.pi / 180
    N = sa / np.sqrt(1 - e2 * np.sin(lat_rad) ** 2)
    T = np.tan(lat_rad) ** 2
    C = e2 * np.cos(lat_rad) ** 2 / (1 - e2)
    A = np.cos(lat_rad) * (lon_rad - lambda0)
    M = sa * ((1 - e2 / 4 - 3 * e2 ** 2 / 64 - 5 * e2 ** 3 / 256) * lat_rad
              - (3 * e2 / 8 + 3 * e2 ** 2 / 32 + 45 * e2 ** 3 / 1024) * np.sin(2 * lat_rad)
              + (15 * e2 ** 2 / 256 + 45 * e2 ** 3 / 1024) * np.sin(4 * lat_rad)
              - (35 * e2 ** 3 / 3072) * np.sin(6 * lat_rad))
    x = 500000 + (N * A * (1 + A ** 2 * (1 - T + C) / 6 + A ** 4 * (5 - 18 * T + T ** 2 + 72 * C - 58 * e2) / 120))
    y = M + N * np.tan(lat_rad) * (A ** 2 / 2 + A ** 4 * (5 - T + 9 * C + 4 * C ** 2) / 24 + A ** 6 * (61 - 58 * T + T ** 2 + 600 * C - 330 * e2) / 720)
    y[latitudes < 0] += 10000000
    return x, y


def rostime_to_datetime(rostime):
    """
    将ROS时间戳转换为Python的datetime对象
    """
    return datetime.datetime.fromtimestamp(rostime.secs + rostime.nsecs * 1e-9)


def fit_rotation_translation(A, B):
    """
    通过最小二乘拟合旋转和平移矩阵
    """
    centroid_A = np.mean(A, axis=0)
    centroid_B = np.mean(B, axis=0)
    AA = A - centroid_A
    BB = B - centroid_B
    H = np.dot(AA.T, BB)
    U, _, V = svd(H)
    R = np.dot(V.T, U.T)
    if np.linalg.det(R) < 0:
        V[:, -1] *= -1
        R = np.dot(V.T, U.T)
    t = centroid_B.T - np.dot(R, centroid_A.T)
    return R, t


# 读取bag文件
bag = rosbag.Bag('2024-12-03-17-11-37.bag')  # 将这里替换为实际的bag文件名

# 提取gps_imu数据
gps_imu_data = []
gps_timestamps = []
for topic, msg, t in bag.read_messages(topics=['/gps_imu']):
    gps_imu_data.append([msg.x, msg.y, msg.z])
    gps_timestamps.append(rostime_to_datetime(t))
gps_imu_data = np.array(gps_imu_data)
num_messages = len(gps_imu_data)

# 提取map_pose数据
map_pose_data = []
map_timestamps = []
for topic, msg, t in bag.read_messages(topics=['/map_pose']):
    map_pose_data.append([msg.x, msg.y, msg.z])
    map_timestamps.append(rostime_to_datetime(t))
map_pose_data = np.array(map_pose_data)

bag.close()

# 使用KDTree进行最近邻时间戳匹配
tree = KDTree([(ts.timestamp(), 0) for ts in map_timestamps])
_, idx_map = tree.query([(ts.timestamp(), 0) for ts in gps_timestamps])

# 对齐点云数据
A = gps_imu_data
B = map_pose_data[idx_map]

# 拟合旋转和平移矩阵
R, t = fit_rotation_translation(A, B)

# 验证变换
B_transformed = np.dot(R, A.T).T + t
error = np.linalg.norm(B_transformed - B, axis=1)
rmse = np.sqrt(np.mean(error ** 2))

# 计算逆旋转矩阵和逆平移向量
R_inv = R.T
t_inv = - np.dot(R_inv, t)

# 从旋转矩阵计算roll, pitch, yaw（以度为单位）
yaw = np.rad2deg(np.arctan2(R_inv[1, 0], R_inv[0, 0]))
pitch = np.rad2deg(-np.arcsin(R_inv[2, 0]))
roll = np.rad2deg(np.arctan2(R_inv[2, 1], R_inv[2, 2]))

# 打印结果
print(f"逆旋转矩阵 R_inv:\n{R_inv}")
print(f"逆平移向量 t_inv:\n{t_inv}")
print(f"最终的旋转平移结果为:")
print(f"x: {t_inv[0]}")
print(f"y: {t_inv[1]}")
print(f"z: {t_inv[2]}")
print(f"roll: {roll}")
print(f"pitch: {pitch}")
print(f"yaw: {yaw}")
print(f"变换后的均方根误差: {rmse}")

# 绘制原始点云和变换后的点云
plt.figure()
# 绘制原始map_pose的x,y坐标（这里假设为雷达定位对应的坐标）
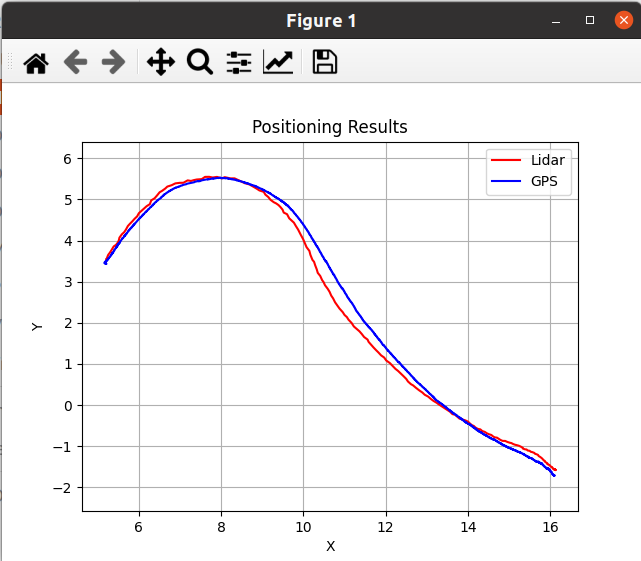
plt.plot(B[:, 0], B[:, 1], 'r-', label='Lidar')
# 绘制变换后与gps_imu对应的x,y坐标（这里假设为GPS定位对应的坐标）
plt.plot(B_transformed[:, 0], B_transformed[:, 1], 'b-', label='GPS')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('定位结果')
plt.legend()
plt.grid(True)
plt.axis('equal')
plt.show()