欧拉降幂 a^b%c ʕ •ᴥ•ʔ

最新推荐文章于 2024-12-12 03:03:57 发布

henucm

最新推荐文章于 2024-12-12 03:03:57 发布

阅读量498

点赞数 1

CC 4.0 BY-SA版权

分类专栏：欧拉降幂数论

本文链接：https://blog.youkuaiyun.com/henucm/article/details/82725457

数论同时被 2 个专栏收录

51 篇文章

订阅专栏

欧拉降幂

5 篇文章

订阅专栏

本文介绍了一种快速计算A^BmodC的方法，利用欧拉公式和快速幂算法，解决了大数幂运算的问题。通过代码实现展示了如何在短时间内处理大规模的数学运算。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Description

Given A,B,C, You should quickly calculate the result of A^B mod C. (1<=A,C<=1000000000,1<=B<=10^1000000).

Input

There are multiply testcases. Each testcase, there is one line contains three integers A, B and C, separated by a single space.

Output

For each testcase, output an integer, denotes the result of A^B mod C.

Sample Input

3 2 4
2 10 1000

Sample Output

1
24

Hint

Source

FZU 2009 Summer Training IV--Number Theory

题意：A^B mod C

欧拉公式不得不说欧拉太强了！！

这道题用的是公式三

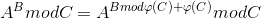
然后就是上代码！

#include<cstdio>
#include<cmath>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<map>
#include<vector>
#define N 750010
#define ll long long
using namespace std;
ll ol(ll x)
{
	int ans=x;
	for(ll i=2;i*i<=x;i++)
	{
		if(x%i==0)
		{
			ans=ans/i*(i-1);
			while(x%i==0)
			{
				x/=i;
			}
		}
	}
	if(x!=1)
	ans=ans/x*(x-1);
	return ans;
}
ll power(ll a,ll b,ll mod)
{
	ll ans=1;
	while(b)
	{
		if(b&1)
		{
			ans=ans*a%mod;
		}
		a=a*a%mod;
		b>>=1;
	}
	return ans;	
}
int main()
{
	ll a,c;
	char s[1000006];
	while(~scanf("%lld %s %lld",&a,s,&c))
	{
		ll ans=0;
		ll tmp=ol(c);
		ll len=strlen(s);
		for(ll i=0;i<len;i++)
		ans=(10*ans+s[i]-'0')%tmp;
		ans+=tmp;
		printf("%lld\n",power(a,ans,c));
	}
	return 0;
}