本文介绍了欧拉函数的性质，包括其积性、与质数的关系及重要性质。阐述了欧拉定理及其扩展，用于解决大数幂运算中的降幂问题。并讨论了当a和n互质或不互质时如何利用欧拉定理和扩展欧拉定理进行计算。最后，提供了欧拉函数的代码实现，包括递推和线性筛两种方法。
大数幂运算指数太大的时候，我们需要进行降幂操作。
首先呢，认识欧拉定理之前 先了解一下欧拉函数
欧拉函数性质
- 若p是一个质数，那么Φ(p)=p-1
- 欧拉函数是积性函数，所以Φ(nm)=Φ(n)Φ(m)
- 若n=p^k且p为质数，那么Φ(n)=p^k-p^(k-1)。（证明：因为p为质数，那么p^k能被p整除的就有p^(k-1）个，如此说来，不能被p整除的就是两者相减咯）
- 当n为奇数时，有Φ(2*n)=Φ(n)
- ∑(d|n)Φ(d)=n 非常重要的性质！！
欧拉定理
我们将欧拉函数写作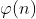
欧拉定理就是a、n为正整数且a、n互质，那么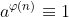 
(mod n)
那么根据欧拉定理的式子，我们可以转化为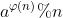 
%n=1
那么既然
最低0.47元/天 解锁文章
扫一扫
484
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
