C++ 找到平行四边形的缺失点(Find the Missing Point of Parallelogram)

给定三个坐标点 A、B 和 C，求缺失点 D，使得 ABCD 可以构成平行四边形。

如果您喜欢此文章，请收藏、点赞、评论，谢谢，祝您快乐每一天。 

示例： 

输入： A = (1, 0) 
        B = (1, 1) 
        C = (0, 1)输出： 0, 0

解释：

三个输入点与点 (0, 0) 形成一个单位正方形输入： A = (5, 0) 
        B = (1, 1) 
        C = (2, 5)输出： 6, 4

如下图所示，可能有多种输出，我们需要打印其中的任意一种。 

如果四边形的对边平行且长度相等，则该四边形称为平行四边形。 

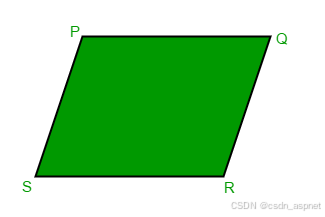
给定平行四边形的三个点，我们就能求出缺失边的斜率以及它们的长度。 
该算法解释如下：
设 R 为缺失点。根据定义，我们有 
 

• PR 的长度 = QS 的长度 = L1 （对边相等）
• PR 的斜率 = QS 的斜率 = M1 （对边平行）
• PQ 的长度 = RS 的长度 = L2（对边相等）
• PQ 的斜率 = RS 的斜率 = M2 （对边平行）

因此，我们可以找到距离 P 点 L1 且斜率为 M1 的点，如下文所述： 

在给定斜率的直线上，找到给定距离的点：

Javascript 在给定斜率的线上找到给定距离处的点：https://blog.youkuaiyun.com/hefeng_aspnet/article/details/149936134
C# 在给定斜率的线上找到给定距离处的点：https://blog.youkuaiyun.com/hefeng_aspnet/article/details/149936112
Python 在给定斜率的线上找到给定距离处的点：https://blog.youkuaiyun.com/hefeng_aspnet/article/details/149936088
Java 在给定斜率的线上找到给定距离处的点：https://blog.youkuaiyun.com/hefeng_aspnet/article/details/149936046
C++ 在给定斜率的线上找到给定距离处的点：https://blog.youkuaiyun.com/hefeng_aspnet/article/details/149935654

现在，其中一个点将满足上述条件，这很容易检查（使用条件 3 或 4）。

以下是上述方法的实现： 

// C++ program to find missing point of a
// parallelogram
#include <bits/stdc++.h>
using namespace std;

// struct to represent a co-ordinate point
struct Point {
    float x, y;
    Point()
    {
        x = y = 0;
    }
    Point(float a, float b)
    {
        x = a, y = b;
    }
};

// given a source point, slope(m) of line
// passing through it this function calculates
// and return two points at a distance l away
// from the source
pair<Point, Point> findPoints(Point source,
                              float m, float l)
{
    Point a, b;

    // slope is 0
    if (m == 0) {
        a.x = source.x + l;
        a.y = source.y;

        b.x = source.x - l;
        b.y = source.y;
    }

    // slope if infinity
    else if (m == std::numeric_limits<float>::max()) {
        a.x = source.x;
        a.y = source.y + l;

        b.x = source.x;
        b.y = source.y - l;
    }

    // normal case
    else {
        float dx = (l / sqrt(1 + (m * m)));
        float dy = m * dx;
        a.x = source.x + dx, a.y = source.y + dy;
        b.x = source.x - dx, b.y = source.y - dy;
    }

    return pair<Point, Point>(a, b);
}

// given two points, this function calculates
// the slope of the line/ passing through the
// points
float findSlope(Point p, Point q)
{
    if (p.y == q.y)
        return 0;
    if (p.x == q.x)
        return std::numeric_limits<float>::max();
    return (q.y - p.y) / (q.x - p.x);
}

// calculates the distance between two points
float findDistance(Point p, Point q)
{
    return sqrt(pow((q.x - p.x), 2) + pow((q.y - p.y), 2));
}

// given three points, it prints a point such
// that a parallelogram is formed
void findMissingPoint(Point a, Point b, Point c)
{
    // calculate points originating from a
    pair<Point, Point> d = findPoints(a, findSlope(b, c),
                                      findDistance(b, c));

    // now check which of the two points satisfy
    // the conditions
    if (findDistance(d.first, c) == findDistance(a, b))
        cout << d.first.x << ", " << d.first.y << endl;
    else
        cout << d.second.x << ", " << d.second.y << endl;
}

// Driver code
int main()
{
    findMissingPoint(Point(1, 0), Point(1, 1), Point(0, 1));
    findMissingPoint(Point(5, 0), Point(1, 1), Point(2, 5));
    return 0;
}

输出 ： 

0, 0 
6, 4

时间复杂度： O（log（log n）），因为使用内置的 sqrt 和 log 函数 

辅助空间： O（1）

替代方法： 

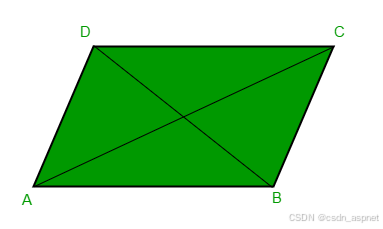
由于对边相等，AD = BC 且 AB = CD，我们可以计算出缺失点 (D) 的坐标：

AD = BC 
(Dx - Ax, Dy - Ay) = (Cx - Bx, Cy - By) 
Dx = Ax + Cx - Bx 
Dy = Ay + Cy - By

参考文献： https://math.stackexchange.com/questions/887095/find-the-4th-vertex-of-the-parallelogram 以下是上述方法的实现：

// C++ program to find missing point
// of a parallelogram
#include <bits/stdc++.h>
using namespace std;

// main method
int main()
{
   int ax = 5, ay = 0; //coordinates of A
   int bx = 1, by = 1; //coordinates of B
   int cx = 2, cy = 5; //coordinates of C
    cout << ax + cx - bx << ", "
         << ay + cy - by;
    return 0;
}

输出： 

6、4

时间复杂度： O(1) 

辅助空间： O(1)

如果您喜欢此文章，请收藏、点赞、评论，谢谢，祝您快乐每一天。