定义2
设(X,ρ)为一个度量空间,实数![]() ,称
,称

![]() 表示的集合,为X中的数y满足条件 y和x的距离小于
表示的集合,为X中的数y满足条件 y和x的距离小于![]()
为度量空间X中以x为中心,以 ![]() 为半径的球形邻域
为半径的球形邻域



定理1
两个球形邻域的交,表示为多个球形邻域的并


![]()

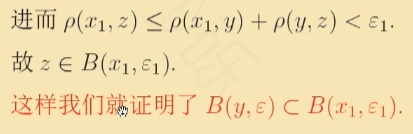
![]()












![]()








![]()




Δ一元二次方程是否有解的判断方程




![]()

左右开根号

 本文探讨了度量空间中的球形邻域定义及其性质,包括球形邻域的交集与并集的关系,并将这些概念与一元二次方程的解的存在判断相结合。通过实例解析,展示了数学理论在实际问题中的应用。
本文探讨了度量空间中的球形邻域定义及其性质,包括球形邻域的交集与并集的关系,并将这些概念与一元二次方程的解的存在判断相结合。通过实例解析,展示了数学理论在实际问题中的应用。
定义2
设(X,ρ)为一个度量空间,实数![]() ,称
,称

![]() 表示的集合,为X中的数y满足条件 y和x的距离小于
表示的集合,为X中的数y满足条件 y和x的距离小于![]()
为度量空间X中以x为中心,以 ![]() 为半径的球形邻域
为半径的球形邻域



定理1
两个球形邻域的交,表示为多个球形邻域的并


![]()

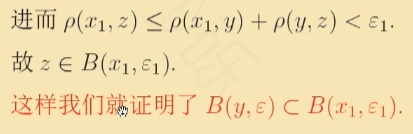
![]()












![]()








![]()




Δ一元二次方程是否有解的判断方程




![]()

左右开根号

 772
772
 8778
8778

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


