工程师 - 卷积的数学定义

卷积（Convolution）是数学、信号处理、图像处理和深度学习中至关重要的运算，其核心思想是通过两个函数的“翻转-平移-叠加”操作，描述它们之间的相互作用关系。以下从不同领域出发，用通俗语言和示例解释卷积的本质与应用。

数学定义：连续与离散卷积

卷积的数学定义是两个函数 f(t) 和 g(t) 的积分运算，描述其中一个函数在另一个函数上的“翻转和平移”叠加效果。

1. 连续卷积

对于连续函数 f(t) 和 g(t)，其卷积 (f∗g)(t) 定义为：

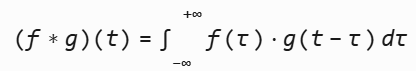
• 关键操作：

  • 翻转：将 g(τ) 关于 τ=0 翻转，得到 g(−τ)；

  • 平移：将翻转后的 g(−τ) 向右平移 t 个单位，得到 g(t−τ)；

  • 叠加：将 f(τ) 与平移后的 g(t−τ) 逐点相乘，再对所有 τ 积分求和。

2. 离散卷积

实际应用中（如数字信号、图像），函数是离散的，卷积简化为求和运算。对于两个长度为 N 的离散序列 f[n] 和 g[n]，其卷积 (f∗g)[k] 定义为：

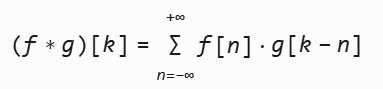
• 关键操作：

  • 翻转：将 g[n] 翻转得到 g[−n]；

  • 平移：将翻转后的 g[−n] 平移 k 个单位，得到 g[k−n]；

  • 叠加：将 f[n] 与平移后的 g[k−n] 对应点相乘，再求和（仅取有效重叠部分）。