工程师 - 模拟滤波器和数字滤波器-优快云博客

本文链接：https://blog.youkuaiyun.com/guoqx/article/details/149523355

数字滤波器专为离散系统设计，其通过数字乘法器、加法器进行运算，改变输入离散信号的数字代码，从而实现对信号频谱的精确控制。数字滤波器的这种特性使其不仅可以在计算机软件中实现，也可以通过大规模集成数字硬件进行构建，提供高度的稳定性和精度。

数字滤波器是一种基于数字信号处理（DSP）技术的算法或系统，其核心功能是对离散时间数字信号（由连续模拟信号采样量化后得到）进行频率选择或特性修改。它通过数学运算（如卷积、差分方程）对信号的各个频率成分进行分析和处理，最终实现对目标频率的保留、抑制或增强。

一、核心原理：离散信号的数学处理

数字滤波器的本质是对离散数字信号进行数学变换。其工作流程通常包括：

1. 采样与量化：将连续模拟信号通过模数转换（A/D）变为离散数字信号（时间离散、幅度离散）。

2. 算法处理：利用预先设计的数学算法（如差分方程、冲激响应）对离散信号进行运算，改变各频率成分的幅度或相位。

3. 重构输出：处理后的数字信号可通过数模转换（D/A）还原为模拟信号，或直接作为数字信号使用（如音频播放、图像显示）。

二，关键参数

描述数字滤波器性能的核心参数与模拟滤波器类似，但需结合数字信号的特性调整：

* 截止频率（fc）：通带与阻带的边界频率（通常定义为增益下降3dB时的频率）。

* 通带波纹（Passband Ripple）：通带内增益的波动幅度（单位：dB，理想滤波器无波纹）。

* 阻带衰减（Stopband Attenuation）：阻带内信号被衰减的最小幅度（如-40dB表示信号衰减为原幅度的 1/100）。

* 群延迟（Group Delay）：信号各频率分量通过滤波器后的延迟差异（线性群延迟可避免信号失真）。

* 阶数（Order）：决定滤波器复杂度和性能的关键参数（阶数越高，频率选择性越强，但计算量越大）。

三，数字滤波器的实现依赖软件算法或硬件平台：

* 软件实现：通过编程语言（如MATLAB、Python、C/C++）编写滤波算法，处理离散信号。

* 硬件实现：通过专用芯片（如DSP、FPGA）或嵌入式系统（如STM32）运行滤波算法，适合实时处理场景（如手机音频处理、工业传感器信号调理）。

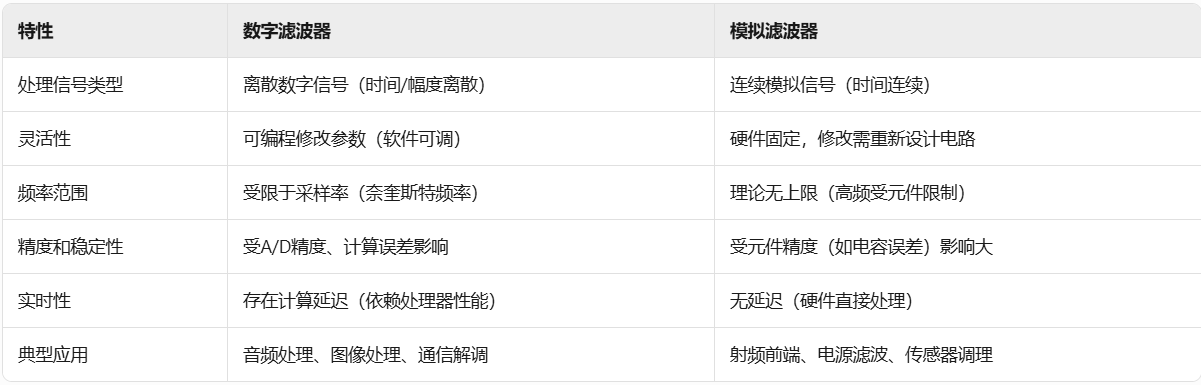
四，与模拟滤波器的对比

总结

数字滤波器是数字信号处理的核心工具，通过算法对离散信号进行频率选择或特性修改。其优势在于可编程性、灵活性和高精度，广泛应用于需要后期处理的场景（如音频编辑、生物医学信号分析）。理解其分类（FIR/IIR）和参数（截止频率、阻带衰减）有助于根据具体需求（如实时性、频率选择性）选择合适的滤波器设计方法。

模拟滤波器是一种基于模拟电子电路（连续时间信号处理）的频率选择装置，其核心功能是对输入的连续模拟信号进行频率筛选——允许特定频率范围内的信号通过（通带），同时抑制或衰减其他频率的信号（阻带）。它是模拟信号处理中最基础的工具之一，广泛应用于通信、音频、传感器信号调理等领域。

模拟滤波器适用于连续时间系统，被广泛应用于离散系统中。模拟滤波器可以分为有源和无源两种类型。有源滤波器主要由运算放大器结合电阻和电容构成，而无源滤波器则主要依赖电阻、电感和电容。然而，模拟滤波器面临诸如电压漂移、温度漂移和噪声等问题，但因其多样化的元件组合，仍然在许多应用中表现优异。

一，核心原理：频率选择性

模拟滤波器通过电路元件（电阻、电容、电感、运算放大器等）的组合，对不同频率的信号产生不同的响应。其本质是利用元件的频率特性（如电容的容抗随频率升高而降低，电感的感抗随频率升高而升高），改变信号中各频率分量的幅度或相位，最终实现对目标频率的选择性传输。

二，关键参数

描述模拟滤波器性能的核心参数包括：

* 截止频率（fc）：通带与阻带的边界频率，通常定义为增益下降至通带最大值的1/2（-3dB）时的频率（如低通滤波器中，高于fc的信号被衰减）。

* 通带带宽（BW）：通带的有效频率范围（如低通滤波器的带宽为0∼fc）。

* 阻带衰减（Astop）：阻带内信号被衰减的最小幅度（单位：dB，如-40dB表示信号衰减为原幅度的 1/100）。

* 纹波（Ripple）：通带或阻带内增益的波动幅度（理想滤波器无纹波，实际滤波器因设计复杂度可能存在小幅波动）。

* 相位响应：信号通过滤波器后的相位变化（线性相位滤波器可保持信号各频率分量的相位关系，避免失真）。

三，分类方式