[USACO06JAN]冗余路径Redundant Paths

题目描述

In order to get from one of the F ($1<=F<=5,000$) grazing fields (which are numbered $1..F$) to another field, Bessie and the rest of the herd are forced to cross near the Tree of Rotten Apples. The cows are now tired of often being forced to take a particular path and want to build some new paths so that they will always have a choice of at least two separate routes between any pair of fields. They currently have at least one route between each pair of fields and want to have at least two. Of course, they can only travel on Official Paths when they move from one field to another.

Given a description of the current set of R ($F-1<=R<=10,000$) paths that each connect exactly two different fields, determine the minimum number of new paths (each of which connects exactly two fields) that must be built so that there are at least two separate routes between any pair of fields. Routes are considered separate if they use none of the same paths, even if they visit the same intermediate field along the way.

There might already be more than one paths between the same pair of fields, and you may also build a new path that connects the same fields as some other path.

题目大意

给你一个无向连通图，问你至少再加多少条边可以使得任意两点间有两条没有一条重合的边的路径。
#Solution
看到这题第一眼，就想到了一个模型，如果这个无向联通图是一棵树的话，那么答案就是叶子节点个数 + 1 / 2, 具体构造方法它咕掉了。
然后想度数为1点个数 + 1 / 2就是答案了。（虽然学校数据水到这样都能AC）
之后被下面这种情况卡到当场去世。

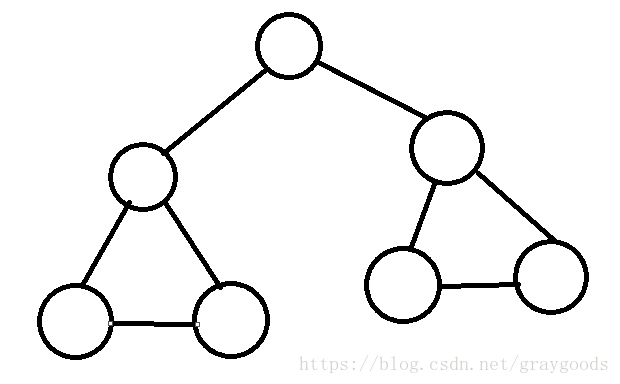
那怎么办呢，通过观察我们可以发现，在一个无向图中，如果出现了一个环，那么这个环上所有的点都满足条件，这样，这些点就可以当做一个点了。
然后我们把在同一个环上的节点缩成一个点，再建出一个新图，就是一棵树了，统计叶子节点个数即可。
之后思考如何缩点，发现题目的要求就是边双联通分量的的定义，直接Tarjan缩点即可。

#include<cstdio>
#include<cstring>
#include<stack>

const int maxn = 100007;  
const int maxm = 500007;

class Map {
private :
    struct Node {
        int u, v, nex;
        
        Node (int u = 0, int v = 0) :
            u(u),
            v(v),
            nex(0) {}
    };
    Node edge[maxm * 2];
    int head[maxn], cnt, dfn[maxn], low[maxn], id[maxn], vis[maxm * 2];
    int n, tot, degree[maxn];
    int col[maxn], sum;
    std :: stack<int> st;
    
public :
    void Init(int x) {
        n = x;
    }
    
    void AddEdge(int u, int v) {
        edge[++cnt] = Node(u, v);
        edge[cnt].nex = head[u];
        head[u] = cnt;
    }
    
    void Tarjan(int now) {
        if (!dfn[now]) {
            low[now] = dfn[now] = ++tot;
            id[dfn[now]] = now;
        }
        st.push(now);
        for (int i = head[now]; i; i = edge[i].nex) {
            int v = edge[i].v;
            if (vis[i]) {
                continue;
            }
            if (!dfn[v]) {
                vis[i] = vis[(i & 1) ? i + 1 : i - 1] = 1;
                Tarjan(v);
                vis[i] = vis[(i & 1) ? i + 1 : i - 1] = 0;
                low[now] = std :: min(low[now], low[v]);
            } else {
                low[now] = std :: min(low[now], dfn[v]);
            }
        }
        if (dfn[now] != low[now]) {
            return;
        }
        sum++;
        while (dfn[st.top()] != low[now]) {
            col[st.top()] = sum;
            st.pop();
        }
        col[st.top()] = sum;
        st.pop();
    }
    
    void Make() {
        Tarjan(1);
    }
    
    int Deal() {
        int res = 0;
        for (int i = 1; i <= cnt; i += 2) {
            int u = edge[i].u, v = edge[i].v;
            if (col[u] == col[v]) {
                continue;
            }
            degree[col[u]]++;
            degree[col[v]]++;
        }
        for (int i = 1; i <= n; i++) {
            if (degree[i] == 1) {
                res++;
            }
        }
        return res;
    }
};

class Solution {
private :
    int n, m, degree[maxn], sum, ans;
    Map mp;

public :
	Solution () {
		Get();
		Solve();
	}
    void Get() {
        scanf("%d %d", &n, &m);
        mp.Init(n);
        for (int i = 1; i <= m; i++) {
            int u, v;
            scanf("%d %d", &u, &v);
            mp.AddEdge(u, v);
            mp.AddEdge(v, u);
            degree[u]++;
            degree[v]++;
        }
    }
    
    void Solve() {
        mp.Make();
        for (int i = 1; i <= n; i++) {
            if (degree[i] == 1) {
                sum++;
            }
        }
        ans = mp.Deal() + 1 >> 1;
        printf("%d\n", ans);
    }
};
Solution sol;

int main() {}

不写主函数是信仰！