1031D - Minimum path

最新推荐文章于 2024-06-12 22:57:04 发布

原创最新推荐文章于 2024-06-12 22:57:04 发布 · 714 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#CF #BFS

CF 专栏收录该内容

3 篇文章

订阅专栏

本文解析了1031D-Minimum path问题，通过动态规划确定最少改变次数使路径字典序最小，再利用BFS寻找最优路径，最后通过DFS逆向输出答案。适用于算法竞赛和路径优化问题。

1031D - Minimum path

题目描述

传送门

题目大意

给你一个 $\times n$ 的只有小写字母的字符矩阵，你要从 $1, 1$ 走到 $n, n$ ，只能往下，往右走，同时你可以改变这个矩阵中的 $k$ 个字符，问你走到 $n, n$ 所经过的路径的最小字典序是多少。
$\le n \le 2000$

Solution

比赛的时候最后5分钟才过去，保我上蓝QwQ

首先这道题要求字典序最小，所以我们改变这个矩阵中的字符，一定是把不是 $a$ 的字符改成 $a$ ，而且我们走一条路径的时候，一定是把所有机会全用到（如果 $k$ 过大就可以全是 $a$ ），并且尽可能地要让前面变成 $a$ 。
所以我们设 $f [i] [j]$ 表示从 $1, 1$ 走到 $i, j$ 全走 $a$ 至少要改变多少次，由于只能向下和向右走，所以 $f [i] [j]$ 只可能从 $f [i - 1] [j], f [i] [j - 1]$ 转移过来。DP复杂度 $O(n^2)$ 。
之后，我们把 $\le k$ 点找出来，找出所有走得最远的点，作为接下来 $B F S$ 的起点（特别地，如果 $k = 0$ 就需要把 $1, 1$ 选出来当作起点）。
进行BFS，我们看图说话：

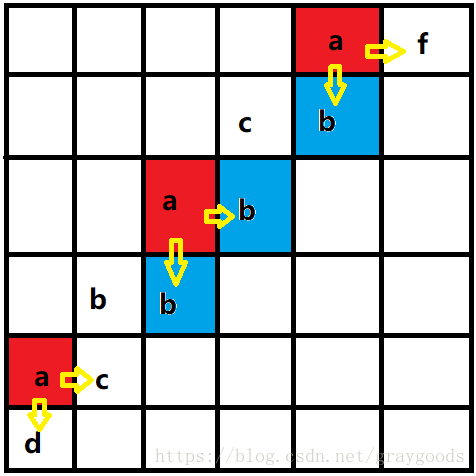
假设红色的点为现在的起点，那么黄色箭头表示现在的的起点能前往的格子，我们找出现在能到达的格子中最小的字符，然后把带有最小字符的格子（也就是上图中的蓝色格子）存起来（同时给这个格子打一个标记，说明这个格子可以当作答案的一步），当作下一次的起点，重复上树的操作知道到达 $n, n$ ，由于我们每进行一次操作，都相当于走了一步，所以最多进行 $n$ 次这样的操作。

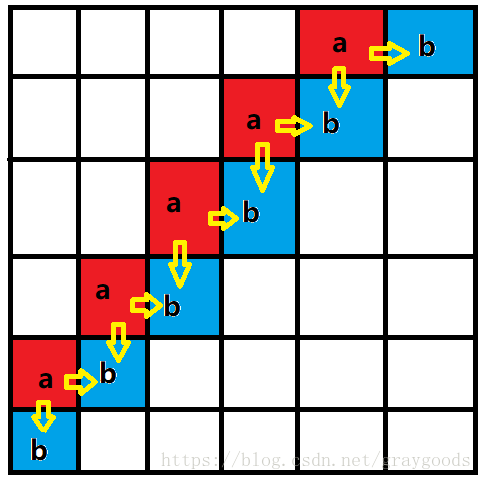
看起来似乎状态是呈指数级增长的，BFS会爆掉，但实际上，我们发现，最坏的情况就是上图的情况，但是每层的情况数最多也只会达到 $n$ 个，所以，BFS的复杂度为 $O(n^2)$
至于输出答案，我们可以从 $n, n$ 进行DFS，这个点上面或者左面哪一个点被打过标记，就往那边走，一直走到最初的起点。
之后输出 $a$ 和找到的路径即可。

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

const int maxn = 2e3 + 7;

class Solution{
private :
    int n, k, cnt;
    char s[maxn][maxn];
    int f[maxn][maxn];
    bool vis[maxn][maxn];
    
    char ans[maxn * 2];
    int tot;

    struct Node{
        int x, y;

        Node (int x, int y) :
            x(x),
            y(y) {}
    };
    
    int now, last;
    std :: queue<Node> q[2], tmp;

    void Make() {
        for (register int i = 1; i + cnt < n + n; i++) {
            char z = 'z' + 1;
            while (!q[last].empty()) {
                Node nd = q[last].front();
                tmp.push(nd);
                q[last].pop();
                if (nd.x < n) {
                    z = std :: min(z, s[nd.x + 1][nd.y]);
                }
                if (nd.y < n) {
                    z = std :: min(z, s[nd.x][nd.y + 1]);
                }
            }
            while (!tmp.empty()) {
                Node nd = tmp.front();
                tmp.pop();
                if (nd.x < n) {
                    if (s[nd.x + 1][nd.y] == z && !vis[nd.x + 1][nd.y]) {
                        vis[nd.x + 1][nd.y] = 1;
                        q[now].push(Node(nd.x + 1, nd.y));
                    }
                }
                if (nd.y < n) {
                    if (s[nd.x][nd.y + 1] == z && !vis[nd.x][nd.y + 1]) {
                        vis[nd.x][nd.y + 1] = 1;
                        q[now].push(Node(nd.x, nd.y + 1));
                    }
                }
            }
            std :: swap(now, last);
        }
    }
    
    void DFS(int x, int y) {
    	if (x <= 0 || y <= 0) {
    		return;
		}
    	if (x + y == cnt) {
    		return;
		}
		ans[++tot] = s[x][y];
		if (vis[x - 1][y]) {
			DFS(x - 1, y);
		} else {
			DFS(x, y - 1);
		}
	}
    
public :
    Solution() {
        now = 1;
        last = 0;
        Get();
        Solve();
    }

    void Get() {
        scanf("%d %d", &n, &k);
        for (register int i = 1; i <= n; i++) {
            scanf("%s", s[i] + 1);
        }
    }

    void Solve() {
        memset(f, 0x3f, sizeof(f));
        f[1][1] = s[1][1] == 'a' ? 0 : 1;
        for (register int i = 1; i <= n; i++) {
            for (register int j = 1; j <= n; j++) {
            	if (i == 1 && j == 1) {
            		continue;
				}
                f[i][j] = std :: min(f[i - 1][j], f[i][j - 1]);
                if (s[i][j] != 'a') {
                    f[i][j]++;
                }
            }
        }
        for (register int i = 1; i <= n; i++) {
            for (register int j = 1; j <= n; j++) {
                if (f[i][j] <= k && i + j > cnt) {
                    cnt = i + j;
                }
            }
        }
        for (register int i = 1; i <= n; i++) {
            for (register int j = 1; j <= n; j++) {
                if (i + j == cnt && f[i][j] <= k) {
                    vis[i][j] = 1;
                    q[last].push(Node(i, j));
                }
            }
        }
        if (q[last].empty()) {
        	vis[1][1] = 1;
        	q[last].push(Node(1, 1));
		}
        Make();
        DFS(n, n);
        for (register int i = 1; i < cnt; i++) {
        	putchar('a');
		}
		for (register int i = tot; i >= 1; i--) {
			putchar(ans[i]);
		}
		putchar('\n');
    }
};
Solution sol;

int main() {}