线性方程组（三）- 向量方程-优快云博客

本文链接：https://blog.youkuaiyun.com/github_40153370/article/details/87894269

本文介绍了向量的定义及其在R2和Rn中的表示，阐述了向量加法、标量乘法的几何意义，并通过实例展示了如何解向量方程。还探讨了Span的概念及其在几何上的解释，包括Span{v}和Span{u,v}所张成的空间。" 113993940,10544391,烹饪原料知识与保藏方法,"['食材知识', '食品保藏', '营养学', '烹饪技巧', '食品安全']

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

小结

向量的定义
向量方程的定义和求解
$v}\boldsymbol{Span\{v\}}$ 与 $u,v}\boldsymbol{Span\{u,v\}}$ 的几何解释

$R2\mathbb{R}^{2}$ 中的向量

仅含一列的矩阵称为&列向量，或简称向量。向量表示一组有序数。
包含两个元素的向量表示为： $w=[w1w2]\boldsymbol{w} = \begin{bmatrix} w_1 \\ w_2 \\ \end{bmatrix}$ ，其中 $w_1$ 和 $w_2$ 是任意实数。
所有两个元素的向量的集记为 $R2\mathbb{R}^{2}$ ， $R\mathbb{R}$ 表示向量中的元素是实数，而指数2表示每个向量包含两个元素。
$R2\mathbb{R}^{2}$ 中两个向量相等当且仅当其对应元素相等。即 $R2\mathbb{R}^{2}$ 中的向量是实数的有序对。
给定实数 $c$ 和 $R2\mathbb{R}^{2}$ 中两个向量 $u\boldsymbol{u}$ 和 $v\boldsymbol{v}$ ，它们的和 $u+v\boldsymbol{u}+\boldsymbol{v}$ 是把 $u\boldsymbol{u}$ 和 $v\boldsymbol{v}$ 对应元素相加所得的向量。 $u\boldsymbol{u}$ 和 $c$ 的标量乘法（或数乘）是把 $u\boldsymbol{u}$ 的每个元素乘以 $c$ ，所得向量记为 $cuc\boldsymbol{u}$ 。 $cuc\boldsymbol{u}$ 中的数 $c$ 称为标量（或数）。

给定 $u=[1−2]\boldsymbol{u}= \begin{bmatrix} 1 \\ -2 \\ \end{bmatrix}$ 和 $u=[2−5]\boldsymbol{u}= \begin{bmatrix} 2 \\ -5 \\ \end{bmatrix}$ ，求 $4u−3v4\boldsymbol{u}-3\boldsymbol{v}$
解： $4u−3v\quad4\boldsymbol{u} - 3\boldsymbol{v}$
$=4u+(−3)v=[4∗14∗(−2)]+[−3∗2−3∗(−5)]=[4−8]+[−615]=[4+(−6)−8+15]=[−27]\qquad= 4\boldsymbol{u} + (-3)\boldsymbol{v} \\ \qquad = \begin{bmatrix} 4 * 1 \\ 4 * (-2) \\ \end{bmatrix} + \begin{bmatrix} -3 * 2 \\ -3 * (-5) \\ \end{bmatrix}\\ \qquad = \begin{bmatrix} 4 \\ -8 \\ \end{bmatrix} + \begin{bmatrix} -6 \\ 15 \\ \end{bmatrix}\\ \qquad = \begin{bmatrix} 4 + (-6) \\ -8 + 15 \\ \end{bmatrix}\\ \qquad = \begin{bmatrix} -2 \\ 7 \\ \end{bmatrix}$

$R2\mathbb{R}^{2}$ 的几何表示

考虑平面上的直角坐标系。因为平面上每个点由实数的有序对确定，所以可把几何点 $(a, b)$ 与列向量 $[ab]\left[\begin{matrix} a \\ b \\ \end{matrix}\right]$ 等同。因此我们可把 $R2\mathbb{R}^{2}$ 看作平面上所有点的集合。
向量 $[3−1]\left[\begin{matrix} 3 \\ -1 \\ \end{matrix}\right]$ 的几何表示是一条由原点 $(0, 0)$ 指向点 $(3, - 1)$ 的有向线段。

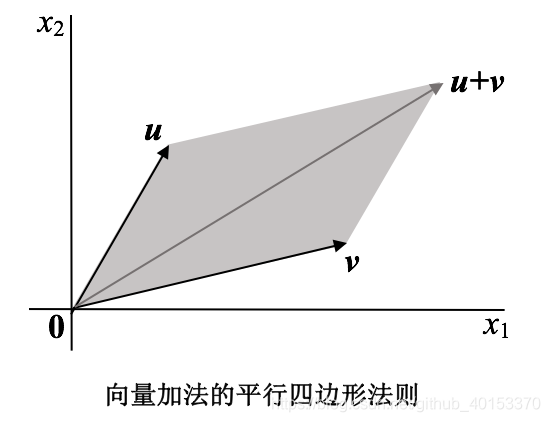
向量加法的平行四边形法则
若 $R2\mathbb{R}^{2}$ 中向量 $u\boldsymbol{u}$ 和向量 $v\boldsymbol{v}$ 用平面上的点表示，则 $u+v\boldsymbol{u} + \boldsymbol{v}$ 对应于以 $u\boldsymbol{u}$ ， $0\boldsymbol{0}$ 和 $v\boldsymbol{v}$ 为顶点的平行四边形的第4个顶点。
在这里插入图片描述

$Rn\mathbb{R}^{n}$ 中的向量

$R3\mathbb{R}^{3}$ 中向量是 $\times 1$ 列矩阵，有3个元素。它们表示三维空间中的点，或起点为原点的箭头。

若 $n$ 是正整数，则 $Rn\mathbb{R}^{n}$ 表示所有 $n$ 个实数数列（或有序 $n$ 元组）的集合，通常写成 $\times 1$ 列矩阵的形式， $u=[u1u2⋮un]\boldsymbol{u}= \begin{bmatrix} u_1 \\ u_2 \\ \vdots \\ u_n \end{bmatrix}$