基于几何区域的群体机器人避障

未知遮挡环境下基于几何区域的群体机器人路径规划

摘要

本文提出了一种基于几何区域的形状控制方法，用于引导具有凝聚力的机器人集群在存在未知障碍物遮挡的环境中向目标移动。在该控制方法中，初始时将机器人集群视为位于一个定义明确的虚拟圆形区域内，从而保持智能体间严格的凝聚力。然而，在行进过程中，为了规避严重受限的障碍物，允许该虚拟圆改变其形状，并在此过程中演化出不同的椭圆形状。本质上，为实现无碰撞路径，这种由圆到椭圆的收缩特性完全取决于群体中的智能体数量，同时也依赖于通过传感器感知的两个最近障碍物之间的距离，以确保收缩后的圆或虚拟椭圆能够顺利通过。因此，形状切换在整个群体行进过程中是一个动态且随机的过程。为实现上述目标，采用了两级分层控制策略。此外，在向目标聚集的过程中，可能发生单个或多个智能体的执行故障。从这一角度出发，所提出的控制律在整个路径中被自适应地更新，使得智能体故障不会阻碍任务的完成。最后，提供了广泛的仿真结果以及硬件实验，以验证所提方案的有效性。

索引词 —自主系统，容错性，避障，形状控制，群体机器人。

一、引言

THE 群体机器人方法涉及大量物理机器人的协调。群体的集体行为源于个体机器人与环境之间的相互作用。形成机器人集群的主要目的是实现一个共同目标，这种现象通常在生物群体中观察到，例如蜂群蜜蜂的[1],集群、鸟类的[2],群集或鱼群的[3],[4]聚集。近年来，针对机器人集群的协同控制已开展了大量研究，例如基于行为的技术[5],[6],、领导者‐跟随者策略[7]–[9]以及虚拟结构方法[10]。这些方法大多并非专为大规模群体设计，因此在智能体数量方面不具备可扩展性。

另一方面，基于人工势场的多智能体路径规划方案[11]–[13]具有可扩展性，使得所有智能体能够以群体形式保持在一起而不发生碰撞，即避免智能体间碰撞。然而，在该方法中，主要挑战是实现期望的智能体间编队[14]，并且该策略不能保证较强的智能体间凝聚力[15]。为了克服上述局限性并控制大量机器人智能体，最近发展出一种基于区域的形状控制策略[14],[16]，其中要求所有智能体在无碰撞的情况下收敛到一个预定义的几何区域内。然而，该方法不允许群体根据环境变化自适应地调整形状的大小和朝向（即未考虑智能体‐环境或群集‐环境交互）[17],[18]。在现实场景中，由于环境通常充满障碍物（静态或动态），显然，为了确保虚拟结构收敛到目标，引导机制应在穿越这些障碍物的过程中随着时间自适应演化[19]。

在此术语下，我们先前的工作[20],提出了一种自适应控制方案，该方案利用基于几何区域的虚拟形状控制技术，在未知遮挡环境中避障。此外，还引入了一种两级分层控制方案[21]；其中运行于每个智能体内部的本地控制器负责驱动每个机器人智能体在虚拟区域内运动，并维持其内部的特定构型。显然，本地控制器并非单一控制器，而是由收敛控制器和编队控制器两个控制器协同工作，以支持我们提出的自适应形状驱动的虚拟区域理念。另一方面，作为监督控制模式的全局控制器，负责通过利用所有智能体的感知信息，在每次迭代中检测附近障碍物并更新虚拟区域的参数。为了改变新创建区域内的智能体间构型，提出了一种新颖的spanning-tree-assisted-shape-matching算法[20]，该算法将更新智能体之间的当前构型，使其位于轮廓内部。

本文进一步扩展了上述工作[20]，以确保可扩展性、智能体间的凝聚性以及实时适用性。此外，在使用群机器人架构时，我们必须始终高度重视系统在智能体故障情况下的系统鲁棒性[22],[23]。一个或多个故障机器人可能导致群体性能[24]下降，并无法满足目标要求[25]。因此，尽早检测和识别系统中可能发生的故障至关重要。准确且及时的故障检测可以显著提高系统的效率、鲁棒性和运行能力[23]。基于此背景，我们总结了本工作的贡献如下。

1) 我们提出了一种多机器人路径规划策略，其中所有智能体都由一个几何虚拟区域引导至目标。在动态变化环境中，虚拟区域的形状可根据智能体的感知信息进行调整。所有智能体必须位于新生成的区域内，以始终保持严格的智能体间凝聚力。我们还证明了所提出的控制方案在面对代理故障时具有足够的鲁棒性。

2) 此外，我们证明了所提方案具有足够的可扩展性。为了支持我们的观点，我们使用多个性能指标（即智能体间凝聚性[26], 旅行方差指数（TVI）[27], 和运行时间计算[8],[27]）将所提研究与一些被广泛引用的群体导航方案（例如领航‐跟随技术及其变体）进行了性能比较。

3) 最后，为了验证所提出控制方案的有效性并支持我们的主张，本文进行了广泛的仿真研究和实时实验。为此，使用了树莓派控制的两轮移动机器人（本地制造）（SonPID），其具有Wi‐Fi（802.11）通信协议，并配备了由五个声呐传感器组成的阵列。我们强调，迄今为止尚未有报道提出过此类能够约束群体保持足够凝聚力的双层鲁棒自适应几何区域导航控制方案。

本文的其余部分组织如下。在第二节中，我们描述了之前关于形状控制方案的方法。在这方面，我们重新全面介绍了局部与全局控制律。基于圆到椭圆的导航策略在第三节中进行了阐述。接着，在第四节中，设计了用于管理智能体故障的更新的控制律。第五节报告了实验的详细结果，以验证所提方案在模拟环境以及实时环境中的有效性。最后，第六节对本文进行了总结。

II. 背景

在本节中，我们将简要描述我们之前关于基于区域的形状控制方案的工作[20]。整体概念以方框图的形式进行拓扑建模，并在图1(a)中展示。考虑一组 N机器人智能体在二维空间中同时向预定义目标T ∈2移动。位于pi ∈2的第 i个智能体的运动动力学可表示为[12]

$$
\dot{p}_i = u_i \quad \forall i={1, 2,…, N} \tag{1}
$$

其中 $u_i$表示第 i个智能体在保持群组内特定构型的同时朝向目标运动的控制动作。因此，控制输入需要建模为一种方式，使得在接近 T的过程中，所有智能体都能避开障碍物，并形成一种swarm状框架，以维持期望模式。为解决这一假设，我们借鉴了基于几何区域的形状控制方案[14]的思想。在本研究中，我们选择一个初始虚拟圆（如假设 1所述），要求所有智能体都聚集在其内部。在移动过程中，圆形参数将根据智能体的感知信息进行更新。为实现这一点，我们采用两级分层控制架构[28]来实现机器人集群的导航。

假设1 ：假设在未知环境中创建一个圆形虚拟结构，其中心位于 $O_c=[x_c, y_c]$，半径为 $r_c$（该半径应依赖于群体中的智能体数量）。

A. 本地控制器

如前所述，本地控制器可被视为一个两级控制器，由收敛控制器和随后的编队控制器组成[见图1(a)]。一旦创建了虚拟边界，每个智能体的本地控制器的第一层（即收敛控制器）将首先被触发，使智能体聚集到新创建的虚拟区域内，如图1(b)所示。当所有智能体都在虚拟区域内收敛后，本地控制器的第二层，即编队控制器，将被激活以实现期望的智能体间编队。因此，第 i个智能体的本地控制器的运动动力学可表示为（详细推导见[20]）

$$
\dot{p} i = -k_i^c(t) \times (p_i(t) - O_c(t)) + k_f \sum {j=1, j \neq i}^{N} \left[\exp\left(-\frac{|p_{ij}|}{[\lambda \circ \Delta]_{ij}}\right) \times (p_i(t) - p_j(t))\right] \tag{2}
$$

其中，$k_i^c(t)$是相关的收敛增益[20]，$O_c(t)=[x_c(t), y_c(t)]$是第$t$个时刻圆形区域的中心，$k_f$是广义构型增益，$|p_{ij}| = |p_i(t) - p_j(t)|$是代理$i$与代理$j$在第$t$个时刻的欧几里得距离，$\lambda \in \mathbb{R}^{N\times N}$是期望的代理间距离矩阵，$\Delta$是相关的邻接矩阵，算子$\circ$表示矩阵逐元素乘法或哈达玛积[29]。因此，项$[\lambda \circ \Delta]_{ij}$将表示从代理$i$到代理$j$的期望距离。

因此，我们可以重申，在本地控制器执行后，所有智能体将向虚拟圆移动，如图1(b)所示。假设在有限时间（τ）内，它们将进入由$[\lambda \circ \Delta]$定义的特定构型的区域内。定理1和定理2将证明这些假设。

定理 1 ：考虑一个由(2)式描述的具有 N个智能体数量的多机器人系统，第 i个智能体将收敛到由 $B_{r_c}(O_c)$定义的虚拟圆内，以形成群体，其中该圆的半径$(r_c)$将为

$$
r_c = \frac{N k_f}{k_i^c} [\lambda \circ \Delta] \times \exp(-1)
$$

并且收敛将在有限时间内发生

$$
\tau = \max_{i \in N} \left{-\frac{1}{2k_i^c} \ln\left(\frac{r_c^2}{2V_i(0)}\right)\right}.
$$

证明 : 该定理的证明可在附带的补充材料中找到。

定理 2 ：考虑由(2)式描述的具有 N个智能体数量的多机器人系统，在圆形区域 $B_{r_c}(O_c)$内，群体的所有成员将保持由$[\lambda \circ \Delta]$定义的特定构型。

证明 ：该定理的分析证明可在我们之前的论文[20]中找到。

因此，在本地控制器的作用下，所有智能体都位于具有期望模式的虚拟区域内。在此导航过程中，感知方案并行运行，以协助估计虚拟区域的下一个位置。该功能完全由专用的全局控制器控制，如图1(a)所示。在进入详细步骤之前，我们考虑两个主要假设。

假设2 ：团队中的每个代理都配备了“m”个距离传感器（如激光雷达[13]和声呐[16]），传感器之间相隔“z”弧度，使得单个代理能够覆盖总共 $2\pi$弧度的范围。

假设3 : 在虚拟区域内，第 i个机器人知道其邻近智能体的相对位置（$N_i$）。

B. 全局控制器

全局控制器（也可视作集中式控制器）的作用是检测前方自由空间（由全局控制器的第一级实现，即obstacle-detection控制器）以及在其中拟合一个虚拟圆，以实现群体在环境中的最安全导航（由全局控制器的第二层，即obstacle-avoidance控制器执行）。整个方案如图 1(a)所示。

在探索基于圆的导航技术时，我们经常意识到，在通过狭窄通道移动时，所提出的方法无法生成圆形参数的下一个足迹。因此，为了克服这一障碍，我们引入了一种基于椭圆的导航方案，即当虚拟圆难以放置在前方感知自由空间内时，通过更新全局控制规则来拟合一个与该圆具有相同面积的等效椭圆轮廓，具体解释见下节。

三、基于虚拟椭圆的导航

在本节中，我们讨论了更新的全局控制策略，以使用椭圆代替圆进行适配。

A. 更新的障碍物检测控制器：全局控制器的第一层级

根据假设2，在第 t个时刻，第 i个智能体周围的感知到的障碍物距离$d_i(t)$将为

$$
d_i(t) = {d_{ij}(t) \mid d_{ij}(t) \geq (r_c - |p_i(t) - O_c(t)|)} \tag{3}
$$

其中$d_i(t)$=[d_{i1}, d_{i2}, …, d_{im}]是第$i$个智能体的感知距离矩阵。基于该信息，可获得相对于全局参考坐标系的预测的障碍物位置 $\tilde{R} i(t)$=[\tilde{R} {ix}(t), \tilde{R}_{iy}(t)]^T

$$
\begin{bmatrix}
\tilde{R} {ix}(t) \
\tilde{R} {iy}(t)
\end{bmatrix}
=
\begin{bmatrix}
x_i(t) \
y_i(t)
\end{bmatrix}
+
\sum_{j=1}^{m} \left[ d_{ij}(t) \cdot
\begin{bmatrix}
\cos[(j - 1)z + \beta_i(t)] \
\sin[(j - 1)z + \beta_i(t)]
\end{bmatrix} \right] \tag{4}
$$

其中$p_i(t)$=[x_i(t), y_i(t)]^T是第$i$个智能体的当前位置，$\beta_i(t)$是该智能体在第$t$个时间点相对于全局参考坐标系的朝向。

在特殊情况下，可能会出现第$i$个智能体被遮挡的情况，使得$|p_i - p_j| > (r_c - |p_i(t) - O_c(t)|)$，这可能导致感知误差。在这种情况下，预测的障碍物位置将根据假设3进行更新

$$
\tilde{R}_i^{(x,y)}(t) = {\tilde{R}_i^{(x,y)}(t) \mid \tilde{R}_i^{(x,y)}(t) \neq p_j(t)} \quad \forall j \in N_i. \tag{5}
$$

现在，$\forall i \in [1, 2, …, N]$，可以计算感知到的障碍物位置（如图2所示）

$$
\tilde{R}^{(x,y)}(t) = [\tilde{R}_1^{(x,y)}(t), \tilde{R}_2^{(x,y)}(t), …, \tilde{R}_N^{(x,y)}(t)]. \tag{6}
$$

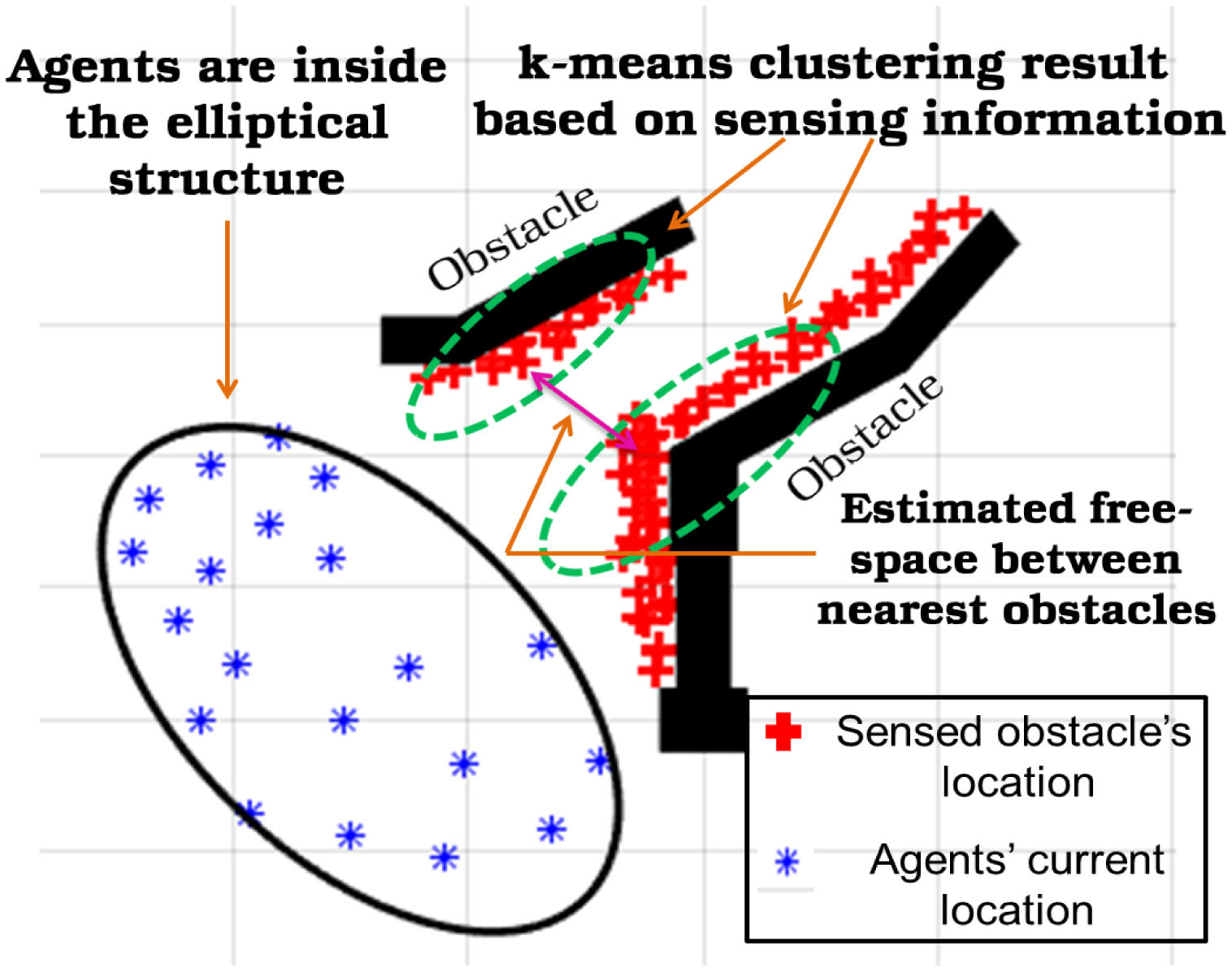
感知后，我们需要确定障碍物之间的最近距离，以适应虚拟圆或椭圆。在这方面，我们特别假设始终存在一条单一路径，群体可通过该路径向目标移动。为了计算感知到的障碍物位置之间的最小距离，我们需要首先将感知点划分为两个簇。为实现此目标，我们使用了著名的k-means聚类算法[30]来找出两个最近障碍物之间的自由空间。聚类后，我们测量各簇的质心，以获得它们之间的欧几里得距离，该距离即为障碍物间的最小距离。图2中展示了一个示例。

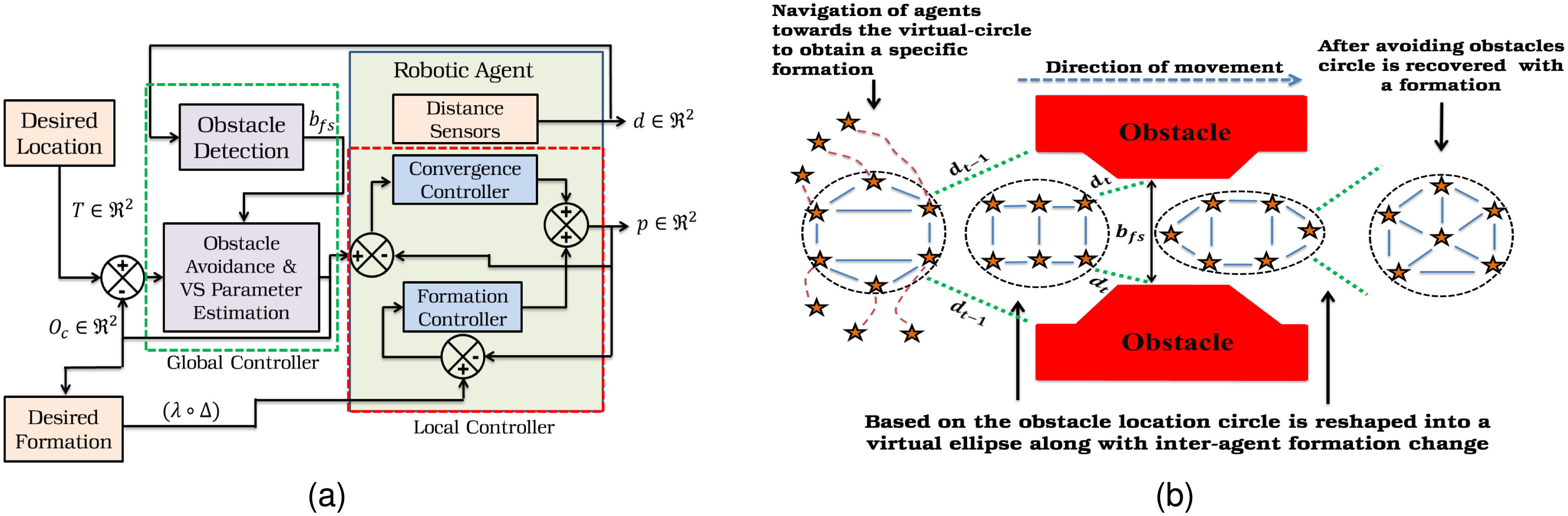
现在，我们假设在第 t个时间，从世界参考坐标系来看，所评估的两个最近障碍物位置分别为 $r_{o1}(t)$和$r_{o2}(t)$，其朝向分别为 $\theta_1$和$\theta_2$，相对于虚拟结构中心 $O_c(t)$，如图3(b)所示，其中 $b_{fs} = |r_{o1} - r_{o2}|$ 是障碍物之间的自由空间，虚拟结构需要被引导通过该区域。

然而，在动态障碍物场景中，该假设可能并非最优，因此，我们需要制定一种通用方法来在这种情况下寻找 $b_{fs}$。假设一个障碍物以恒定速度移动，并且位于群体的感知范围内。因此，在第 $t_1$个时间（$t_1 \in t$），所感知到的障碍物的预测位置为 $\tilde{R}^{(x,y)}(t_1)$，使得 $\tilde{R}^{(x,y)}(t_1) = {r_1, r_2, …, r_n} \in \mathbb{R}^{2\times n}$，且$[r_{o1}(t_1), r_{o2}(t_1)]$ 为最近障碍物位置[见图3(b)]。为了将一个虚拟圆/椭圆拟合到感知自由空间（$b_{fs}$）内，相对于 $\tilde{R}^{(x,y)}(t_1)$的每个元素，点$[r_{o1}(t_1), r_{o2}(t_1)]$的中点的平均欧几里得距离（AD($t_1$)）可以计算为

$$
AD(t_1) = \frac{1}{n} \sum_{i=1}^{n} \left{ |r_i - R| \mid r_i \in \tilde{R}^{(x,y)}(t_1) \right} \tag{7}
$$

其中 $R = \frac{r_{o1}(t_1) + r_{o2}(t_1)}{2}$是点$[r_{o1}(t_1), r_{o2}(t_1)]$的中点，$n$为感知到的障碍物数量。在第 $t_2$个时间（即 $t_2 > t_1$）进行类似的分析，考虑与之前相同的中点(R)。假设其对应的值为 $AD(t_2)$。现在，为了估计第 $t_2$个时间时环境中自由空间($b_{fs}(t_2)$)的大小，执行以下操作：

$$
b_{fs}(t_2) = |r_{o1}(t_1) - r_{o2}(t_1)| \quad \text{if } AD(t_2) \geq AD(t_1). \tag{8}
$$

现在，如果$AD(t_2) < AD(t_1)$，即移动障碍物遮挡了估计的自由空间，则将对第$t_3$次重复执行与(7)和(8)中相同的步骤。一旦自由空间被正确估计，我们的下一个目标是将一个圆形或椭圆轮廓放置在该区域内。

B. 更新的避障控制器：全局控制器的第二层级

为了适应感知自由空间内的虚拟区域，需要激活全局控制器的第二层。该专用控制器的主要目的是确定是拟合一个圆还是用椭圆替代，并相应地更新结构参数[31]。放置圆的方法将遵循我们之前论文中所述的相同步骤[20]。

然而，为了拟合椭圆，控制器需要根据可用自由空间重新更新结构参数，这将在下文重点说明。图3(a)展示了一个代表性虚拟椭圆，其中图3(a)，$O_e(t)=[x_e(t), y_e(t)]$为椭圆中心的位置，$v_e(t)$是朝向目标的速度向量$T(x_g, y_g)$，$\theta(t)$为椭圆长轴的朝向

C. 更新的构型控制器：本地控制器的第二级

为了在未知遮挡环境中实现大规模机器人群体的可靠高效导航，一种可行的方法是让智能体靠近队友，从而显著降低不同群体之间可能产生的干扰风险[12]。这种独特特性通常在生物系统中被观察到[1]–[4]。在群体机器人框架中，这一假设被称为智能体间凝聚性。在本研究中，为了达到类似目标，我们对构型控制器进行改进，使得随着智能体数量增加，群体能够保持一定程度的凝聚力。因此，(2)被修改为

$$
\dot{p} i = -k_i^c(t) \times (p_i(t) - O_e(t)) + k_f \sum {j=1, j \neq i}^{N} \left[\exp\left(-\frac{|p_{ij}|}{[R_s \circ \Delta]_{ij}}\right) \times (p_i(t) - p_j(t))\right] \tag{12}
$$

其中假设 $R_s$为团队中每个机器人在虚拟区域内为避免智能体间碰撞并保持强智能体间凝聚性，需与其邻近智能体保持的最小距离。定理3已给出以证明上述假设的合理性。

定理3 ：考虑一个包含 N个智能体的机器人系统，如(12)所示，位于椭圆形虚拟区域$B_{re}(O_e)$内，其长轴和短轴分别为 $a(t)$和 $b(t)$，第 $i$个智能体应与其邻近智能体保持一定距离 $R_s$，以实现稳定性

$$
|p_{ij}| \geq [R_s \circ \Delta]_{ij}
$$

群体中的所有成员都将在 $B_{re}(O_e)$内实现最大凝聚性，如果

$$
R_s = \sqrt{\frac{a(t) \times b(t)}{N}}.
$$

证明 : 该定理的证明可在所附的补充材料中找到。

IV. 代理故障处理

在任何类型的多机器人路径规划问题中，主要障碍是使系统具备容错性[22],[24], ，即一个或多个智能体的故障不应妨碍任务的完成。在机器人领域，智能体故障主要由感知故障或执行故障引起[22],[23]。在我们的方案中，感知故障可以通过监督控制器轻松处理，因为在导航过程中，每个机器人都需要向控制器传输感知信息。然而，在发生执行故障[25],时，机器人可能无法继续前进，但仍会向监督控制器发送错误信息，这可能会对虚拟结构下一个足迹的评估造成严重问题。

为了处理这一问题，我们在全局控制器中增加了一个决策模块，以便尽早检测智能体的故障。该模块在每次迭代中评估所有智能体相对于虚拟结构中心的误差裕度（e(t)）（$O_e(t)$）。因此，对于第 $i$个智能体，在第 $t$个时间的误差裕度（$e_i(t)$）将为

$$
e_i(t) = p_i(t) - O_e(t) \quad \forall i \in N. \tag{13}
$$

当代理内部发生执行故障时，误差裕度的时间导数仅由虚拟区域中心的相对速度决定。根据此信息，可轻松识别出故障代理。在检测到故障后，需要修改虚拟区域的结构信息以减少冗余区域需求。因此，控制输入 $u_a$将从(11)被修改为

$$
u_a = \frac{r_c^2}{u_b} \times \frac{N - N’}{N} \tag{14}
$$

其中$N’$表示失效代理的数量。

为了展示所提出控制器的性能，后续部分提供了软件仿真以及硬件实现。

V. 结果与讨论

结果部分分为两部分：第一部分展示了软件仿真结果以及对比研究，第二部分包含了基于树莓派控制的两轮移动机器人的实时实验。

A. 软件仿真

仿真在MATLAB 2015a软件环境中进行，处理器为 Intel-Core i7，配备16 GB内存。在此仿真研究中，我们设计了一个面积为 $80 \times 80$单位²的迷宫状遮挡环境，该环境中包含多个具有狭窄通道的障碍物，如图4所示。本研究中选择的参数值如下（见表I）。

1) 案例1. 基于椭圆的导航：

在此仿真研究中，一个由 50个机器人组成的团队应位于预定义虚拟圆形区域内，如图4中的“1”所示。为了将所有智能体容纳在内部以获得较强的智能体间凝聚力（图4中的“2”），初始轮廓已被收缩。为避免狭窄通道，该圆在全球控制器的执行下被重塑为椭圆（3,4,5”在图4中）。最终，所有智能体大约在$t= 150$s时到达目标位置。

2) 案例2. 代理故障：

为了研究所提出的控制动作在代理故障期间的性能，已在与前一节所述相似的环境中对 50个代理进行了仿真。整个结果如图5所示。在$t= 5$ s时，所有智能体在本地控制器的执行下向预定义的虚拟区域移动，以获得较强的智能体间凝聚性，如图5(a)所示。为避开障碍物，初始结构在$t= 14$ s时被重塑为椭圆[见图5(b)]。突然，团队中的少数智能体发生执行故障，但全局控制器尚未识别该故障。因此，收缩的椭圆结构被更新，如图5(c)所示。一旦失效代理被识别，全局控制器会更新一个新的椭圆轮廓，其面积小于前一个[见图5(d)]。在$t= 160$ s时，展示了另一个实例，其中一些智能体无法继续移动，并被相应的控制器正确检测到[见图5(e)]。最终，所有智能体在$t= 250$s时到达目标位置。

B. 性能评估

在本节中，我们分析了提出的控制器以及代理故障处理策略的性能。此外，为了研究所提方案的有效性，将智能体间凝聚性和TVI[27],[35]与一些近期文献进行了比较。结果如图6所示。

在比较虚拟区域的评估面积和轴长之前，我们想指出，我们的所有结果，如图6(a)所示，均是在第五节第V‐A节所述的未知环境中，使用50个代理进行模拟的。在导航过程中，虚拟区域的平均评估面积为57.65单位，标准差为1.09单位。因此，可以认为在探索过程中虚拟区域的计算面积几乎相同。为了比较智能体发生故障时虚拟区域的评估面积，观察到在5%、10%和20%的代理故障情况下，虚拟结构的最终计算面积分别为55.19、52.56和47.80单位，这与我们的理论结果(14)基本一致。从这一结果可以看出，在代理故障场景下，所提出的控制器表现符合预期。在比较上述各种情况下虚拟区域的轴长时，观察到当所有障碍物都被绕过之后，虚拟结构已重塑为一个圆，即椭圆的长轴和短轴收敛至相同的值，如图6(a)所示。

为了分析智能体间凝聚性，我们计算群体在所有迭代中的结构密度[26]。如果群体中两个智能体之间的欧几里得距离大于或等于 $R_s$ 且小于 $2R_s$ （见定理3），则认为这两个智能体是凝聚的。因此，结构密度($D(t)$)可以定义为凝聚链接数量与最大连接数（在丢弃自环之后），如下方公式所示：

$$
D(t) = \frac{\sum_{i=1}^{N}\sum_{j=1, j \neq i}^{N} g_{ij}(t)}{N(N - 1)}; \quad g_{ij} =
\begin{cases}
1 & \text{if } 2R_s > |p_{ij}| \geq R_s \
0 & \text{otherwise}
\end{cases} \tag{15}
$$

结果如图6(b)所示。从图中可以看出，当障碍物密度较高时，即机器人组完全被遮挡时，结构密度在我们所提出的方法中达到最大值。这确保了强大的代理间连接，从而最大化凝聚力。与其他技术相比，当智能体在移动过程中没有内部通信时，观察到最低的智能体间凝聚力[36]。在另一项研究[27],中，由于智能体在向目标推进过程中的自组织原则，凝聚力被发现有所降低。

为了分析行驶时间，我们利用了TVI[27]的概念，并结合群体中不同数量的智能体。它定义了所有智能体在导航过程中行驶距离的变化（即 $N$）。因此，其值可在 $1/N$（最差情况）到1（最佳情况）之间波动。TVI（LV）可解析地定义为[27]

$$
LV = \frac{(\sum_{i=1}^{N} p_i)^2}{N \times \sum_{i=1}^{N}(p_i)^2}. \tag{16}
$$

在我们的分析中，我们观察到，在所提出的方法中，随着智能体数量增加，TVI的值接近1。另一方面，对于无智能体间通信的情况[36] LV，其性能正在恶化。类似地，对于自适应组织方法[27], ，随着团队中智能体数量的增加，TVI逐渐下降。

C. 硬件实现

所提出的技术应用于无人地面车辆（UGV）模型（SonPID），这些模型通过运行本地控制器的基于树莓派的1.4 GHz ARM四核处理器进行控制。802.11 WiFi无线通信模块提供了UGV与中央服务器之间的通信通道，全局控制器在中央服务器上运行。在此控制方法中，每个UGV只需知道虚拟区域中心的坐标信息即可触发本地控制器。为了感知最近障碍物，每个机器人配备了五个间距为 450的超声波模块。采集到的声呐数据被传输至Pi板，并通过WiFi与中央服务器共享。根据这些感知信息，估算出虚拟结构的下一个足迹。

为了评估所提出的策略在复杂环境中的性能，我们进行了多次实验，实验中团队机器人的数量各不相同。该环境的尺寸为 $400 \times 175$厘米²，其中包含静态障碍物、边界和移动障碍物（例如可编程玩具车）。其中一个实验结果如图7所示。在此实验中，我们使用了六台两轮移动机器人。

从初始位置[（如图7(a)],所示）开始，所有智能体通过本地控制器的执行被触发。因此，所有机器人尝试聚集到虚拟椭圆区域内[（参见图7(b)],），而在最高层，全局或监督控制单元根据所有机器人的感知信息生成控制律。为了避开障碍物（包括静态和动态障碍物），如图所示，系统生成了多个相同面积的虚拟椭圆轮廓。具体而言，在 $t= 219$秒时，形成了一个狭窄椭圆区域（其长轴长度远大于短轴），为了适应狭窄通道，控制律迫使机器人形成一条直线[参见图7(c)]。最终，所有智能体成功到达目标位置。

本工作的基本前提是，在所有迭代中，虚拟区域的面积将保持恒定。然而，可以预见的是，传感器引起的感知不准确性可能会改变实际场景中的相同面积要求。为了分析这一事实，我们评估了上述实验中虚拟区域的面积，并将其与仿真结果进行了比较。我们观察到，虚拟区域的平均评估面积约为32.07 cm²，标准差为0.14 cm²,，由此得到变异系数（CV）为0.02。另一方面，在仿真研究中，CV值约为0.001（平均面积和标准差分别为32.067和 0.0074 cm²,），如图8(b)所示。导航过程中主轴和次轴的长度也在图8(a)中展示。从结果可以看出，在硬件实验中，虚拟区域的面积仅有轻微变化（并且也在相当可接受的范围内）。此外，为了对数据（即虚拟区域的评估面积）进行统计分析[，参考图8(c)],可以看出，随着团队中智能体数量的增加，虚拟区域的面积变化正在减小。这一模式在理论上可以得到证实。其背后的原因是，随着智能体数量的增加，实时感知点的数量也随之增加。因此，机器人感知过程相关的估计误差（正/负）几乎被抵消（理想情况），或显著降低（实际情况）。因此，我们发现，在本工作中，我们能够在硬件实验与软件仿真之间建立非常强的统计相关性。通过这些分析，我们可以得出结论：我们提出的控制策略对传感器噪声具有令人满意的免疫力。换句话说，本文合成的控制算法在应对传感器噪声方面表现出较强的鲁棒性。

为了检验所提出的策略在仿真和硬件实验中的有效性，我们评估了群体到达目标位置的运行时间，且具有可扩展性。团队中的智能体在相同环境中，如图7所示。为了进行比较，我们在当前工作中借鉴了领导者-跟随者框架[8]的概念，其中虚拟区域的调整由基于树莓派（4 GB内存）的领导者机器人完成。因此，全局控制器位于该机器人内部，本实验中未使用额外的集中式控制器。结果列于表II中。

从结果可以看出，尽管领导者‐跟随者方法能够成功实现目标，但其耗时比所提出的集中式控制方法更长。

六、结论

在本文中，我们将基于几何区域的机器人集群形状控制技术扩展到未知环境中以实现避障。为实现这一目标，最初考虑使用一个虚拟圆形区域，用于容纳所有智能体，并使其在轮廓内保持较强的智能体间凝聚力。为了躲避障碍物，将虚拟区域修改为具有等效圆形面积的椭圆。所有智能体被分布式地安置在新创建的区域内，以保持强凝聚力。此外，为应对导航过程中出现的智能体故障，所提出的系统能够识别故障机器人，并相应地更新虚拟自适应地获取区域信息。为了说明所提控制动作的性能，提供了多种场景下的大量仿真结果。对比结果表明了所提方案的有效性。此外，该技术还在真实环境中通过一组两轮移动机器人进行了验证。未来的工作包括将虚拟结构划分为多个子结构，以智能地绕过障碍物。