微分代数几何基础（1）

最新推荐文章于 2025-09-21 10:12:54 发布

原创最新推荐文章于 2025-09-21 10:12:54 发布 · 1.6k 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#线性代数 #学习 #几何学 #抽象代数

经典密码专栏收录该内容

14 篇文章

订阅专栏

四. 伪除法（Pseudo-division)

前言

吴文俊（1919-2017）曾出版《数学机械化》一书，旨通过计算机来分析数学问题，将方程求解与自动化推理结合起来。先生可称之为人工智能的先驱，首创符号主义，为铭记其贡献，现有冠名的奖项“吴文俊人工智能科学技术奖”。吴文俊，华罗庚，钱学森也是新中国首批获得国家自然科学一等奖的三位得主。

一. 特征列方法

构造性代数几何是通过构造性的观点来研究方程组。Van der Waerdern-Weil Style就是利用几何离散点，通过母点（generic point）以及特定化（specialization）作为主要的工具。其中最主要的构造性方法就是使用特征列方法（包含三角化方法）。

现比较Grobner基方法和特征列方法。

Grobner方法：消项，计算Spoly消去首项
特征列方法：伪除法消去主变元，零点分解

构造性的过程可见如下图：

举例 1

元朝年间，朱世杰曾在《四元玉鉴》中提出一个三变量二次的例子，如下：

$P_1=xyz-xy^2-z-x-y$

$P_2=xz-x^2-z-y+x$

$P_3=z^2-x^2-y^2$

利用升列和特征列形成并集如下：

其中 $C_1,C_2,C_3$ 表示如下：

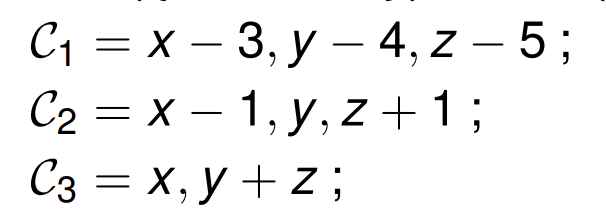
二. 微分代数几何的基本定义

多项式系数的域F代表基域。 $X=(x_1,x_2,\ldots,x_n)$ 为变量集合， $x_1<x_2<\ldots<x_n$ 称为变量的自然序（以角标确定大小序）。

设某个多项式 $P\in F[X]$ 。列举出所有重要的定义：

$deg(P,x_i)$ ：P关于 $x_i$ 的次数;
$clc(P)$ ：P的类（class），P中出现的 $x_c$ 的最大下标C。特例当P=0时，定义cls(P)=0;
$lvar(P)$ ：P的主变元。若cls(P)=c时， $lvar(P)=x_c$ 。此简写的全称为leading variable；
$deg(P)$ :此定义等于 $deg(P,x_c)$

举例 2

若 $P=2x_1^2+2x_3^3+x_2x_3^2+x_1x_2$ ，求 $lvar(P),cls(P),deg(P)$ 。

解：

$lvar(P)=x_3,cls(P)=3,deg(P)=3$

三. 多变元多项式的单变元形式

类为c>0的非常量多项式P可以写成如下正则形式：

$P=I\cdot x_c^d+x_c$ 低次项

正则形式可以看成关于 $x_c$ 的单项式。令 $c=cls(P)>0,d=deg(P)>0$ ，则I称为P的初式(initial)记为init(P)，低次的部分称为P的尾式。

举例3

令 $P=2x_1^2x_2x_3^3+x_2x_3^2+x_1x_2$ ，求cls(P)，主变元，初式I，尾式Q

解：

$P=Ix_3^3+Q$ ，由此 $cls(P)=3$ ,主变元 $x_3$ ，初式I为 $2x_1^2x_2$ ，I的本质也是一个多项式，尾式Q为 $x_2x_3^2+x_1x_2$ 。

四. 伪除法（Pseudo-division)

伪除法过程一共有四步如下：

设P,Q为非零多项式,c=cls(P),d=deg(P),I=init(P)
令R=Q，重复操作 $R:=IR-b_mx_c^{m-d}P$ ，其中 $b_m$ 是R关于 $x_c$ 的首系数，重复直到 $m=deg(R,x_c)<d$
观察重复过程，每次操作后m都是严格递减的。所以这个过程在某个阶段必定会终止
最终可得 $I^SQ=GP+R$

上述步骤中 $G,R\in R_q$ ，s是非零整数。最终的R=0或者 $deg(R,x_c)<d$ ，此时的R称为Q关于P的伪余式（Pseudo-remainder)，记作prem(Q,P)。