详解隐私放大（Privacy amplification）

写在前面：本文适合初学者。

Alice和Bob在进行密钥提取（key distillatiobn）时，会依次按顺序经历如下步骤：

优势建立-------- 信息调和 (Information Reconciliation)-------隐私放大 (Privacy Amplification)

可以看到隐私放大通常放在最后一步。

简单来讲，在经历信息调和后，Alice和Bob会获得一个共同的序列S（比如n比特长），经历隐私放大后，该序列被压缩为k比特长，于此同时Eve不会获得任何有用信息。

备注：在安全领域，Alice代表合法发送者，Bob代表合法接收者，Eve代表非法窃听者。

综合以上分析，我们来看看官方对于隐私放大的定义：

The role of privacy amplification is to process the sequence S obtained by Alice and Bob after reconciliation to extract a shorter sequence of k bits that is provably unknown to Eve.

接着我们来看三个平凡（trivial）的例子。

1. 如果Eve对序列S本身就一无所知，那么就不需要利用隐私放大技术，序列S本身就可以作为密钥（不要忘记隐私放大的本质就是想提取出一个私密的密钥）；
2. 如果Eve对序列S完全了解的话，则合法双发无法提取出任何有用的密钥；
3. 序列S一共n比特长，如果Eve知道其中的m比特，那么说明S还剩下n-m个比特可以作为私钥（secret key）;

但实际情况并非如此简单，比如我们无法确定Eve到底知道哪些比特，又到底不知道哪些比特。换句话说，合法用户只知道Eve能获得信息量的一个上界，并不能直接对应S的比特位置，难点可总结为：

Alice and Bob know a bound for Eve’s information that cannot be tied to bits of S directly.

当然，这个上界(bound）将决定Alice和Bob到底能提取多少比特的密钥。

补充密钥提取：从不完全随机的原始密钥（可能部分泄露给 Eve），提取出一个接近均匀分布、Eve 几乎无信息的秘密密钥。

在优势提取（advantage-distillation）与调和（reconciliation）的过程中，Eve也可以观察随机源，同时Alice与Bob在公开信道（public channel）上也会交互一些信息（message），这些信息Eve也能看到。

基于这些观察（observations）,Eve也可能计算出.

原始序列S最多能包含多少“不确定性”？

根据香农熵理论，这不就是H(S)。以防忘记，熵的计算公式如下：

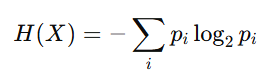
其中代表第i个事件的概率。

由此可推论，只要Eve获得信息量少于H(S)，那么就说明他估计出的在某些位置跟S一定不一样。

巧的是，Eve也不知道具体哪些位置的比特会不一样。

那么事情就好办了，我们可以执行如下图的操作：

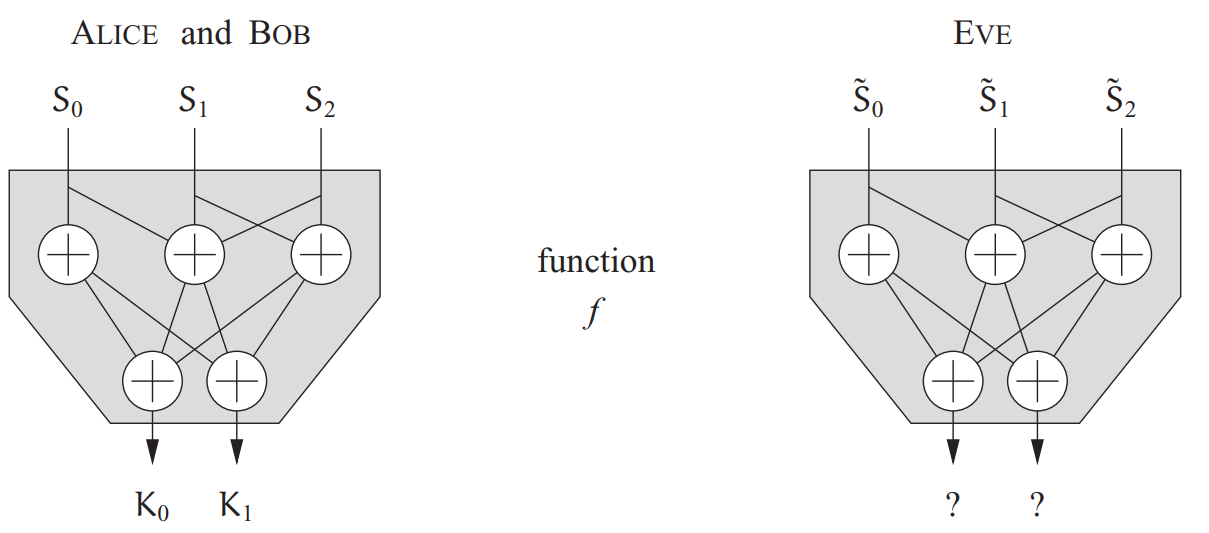
在该图中，Alice,Bob和Eve都可以对各自的序列S与执行函数f的操作。其中代表第0位置的比特（按照代码风格，从第0位置开始，然后第1位置，以此类推）。

函数f一般是公开的。由此获得的密钥可表示为：

由于输入的S与不同，图中左右两边的输出也会不一样。

只要我们能找到一个合适的函数f，则可以保证Eve估计的错误（error）在变换中被不断传播（propagate），导致最后他对K一无所知。

其中函数f可看成一种确定性的变换（deterministic transformation）,在变换中可以混淆（shuffle），也可以移除（remove）部分比特。

这中间的变换只要足够复杂，Eve也就无法预测其误差会如何扩展，从而影响最终的输出。

现在可能有两个问题。

一个是：这种函数变换现实中存在吗？

另一个是：如果让所有输出都能等可能，那么Eve则完全不知道密钥，能实现吗？

答案是可以的：直接利用哈希函数（hash function）。

在密钥提取的过程中，相比香农熵，有两个熵更重要：

1. 碰撞熵（collision entropy）
2. 最小熵（min-entropy）

其实碰撞熵就是阶数为2的Renyi熵。我们可以先看定义。对于任意离散的随机变量X，碰撞熵定义为：

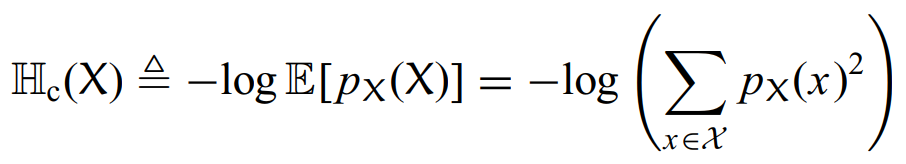
接着我们看Renyi熵的公式：

其中α代表阶数，可以发现当其为2时，公式就回到了刚才的碰撞熵！

接着可以再补充一下最小熵的公式：

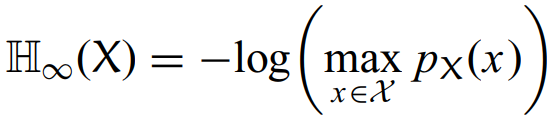
对于这两种熵的具体分析与理解，先买个坑，后续再慢慢更新。