目录
KL散度就是论文中经常出现的Kullback-Leibler Divergence。本文主要关注互信息与KL散度之间的关系。
一. 互信息(Mutual Information)
首先看看如何理解互信息。
直观上,互信息可以衡量两个随机变量之间的关系。既然有两个随机变量X与Y,可以先假设都为离散的(连续的变量也可以,只需要将后续的求和改成积分即可)。
X与Y的联合分布为p(x,y)。为防止有小伙伴忘记,联合分布与条件分布的公式如下:
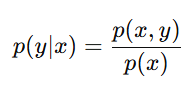
其中分母p(x)则表示边缘分布(marginal distribution)(有时也叫边际分布),可以计算为:
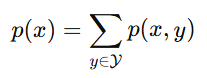
既然变量X能计算,变量Y的边缘分布也可以计算为:
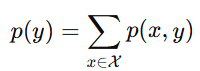
到此,我们就可以定义互信息的公式了,如下:
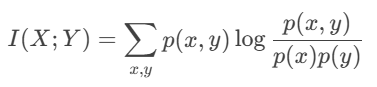
公式有了,怎么理解呢?
先看对数里面p(x,y)/p(x)p(y),不就是联合分布p(x,y)与边缘分布p(x)与p(y)乘积的比值嘛。
再看对数外面,x,y求和与概率p(x,y)放一起,这与期望有点像。
总结I(X;Y)的理解:联合分布p(x,y)与边缘分布乘积p(x)p(y)之间的对数比值的期望。
二. KL散度
接着我们来看KL散度的理解。
KL散度其实就是用来衡量两个概率分布之间的差异。
既然有两个概率分布,我们此处假设为P与Q,一般来讲这两个分布需要在同一个概率空间上。
备注:概率空间(probability space):一般代指样本空间,也就是变量可以取哪些值
那么KL散度的定义公式可以表示为:
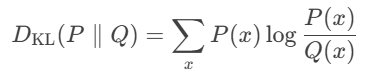
我们来看一种特殊的情况,比如概率P与概率Q完全相同时,也就是P=Q时会发生什么呢?
带入公式包含log1,也就是KL散度可以取0.
三. 从联合分布看待互信息与KL散度之间的关系
在刚才的讨论中,我们将互信息与KL散度的理解放一起:
- 互信息:衡量两个随机变量之间的关系;
- KL散度:衡量两个概率分布之间的差异;
这也太像了吧。
回看之间互信息的公式。如果将分母的p(x)p(y)整体上看成Q,将分子的p(x,y)整体看成P,这不就是KL散度的公式!
为了更加“数学化”,我们也可以将刚才的等效性表达为公式,如下:
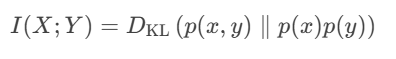
那么就可以从另一个角度来理解互信息了。
互信息:联合分布p(x,y)与边缘分布乘积p(x)p(y)之间的KL散度!
盯着KL散度括号内的公式观察。如果X与Y独立的话,两者相除不就为1了!这与我们以前学习的独立假设相关。
那么实际上,互信息还可以衡量联合分布与独立假设之间的差异。(不要忘记KL散度就是用来衡量两个分布之间的差异)。
四. 从条件分布看待互信息与KL散度之间的关系
接下来我们开始捣鼓互信息的公式。首先回顾其公式为:
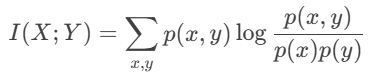
首先联合分布可以转为条件分布,也就是p(x,y)=p(x)p(y|x),带入原公式的分子与求和符号的后面,可得:
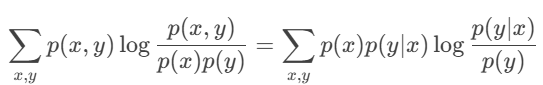
注意分子与分母约掉了一个p(x)。
接着求x,y的求和裂开,可得到:
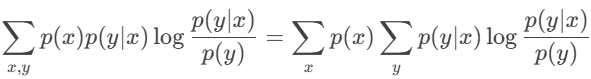
观察y求和的式子,将p(y|x)看成概率P,将p(y)看成概率Q,这不又是KL散度:
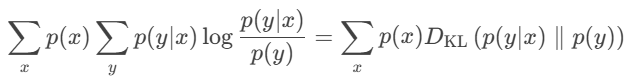
综合以上公式,互信息与KL散度之间的关系,则可以表达为:
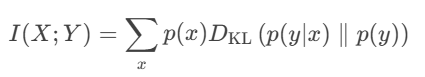
互信息是具有对称性的,换句话说,X与Y本身就是随机变量,互换位置也没问题,那么又可以得到:
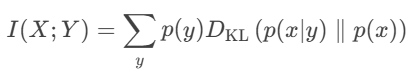
到此,我们也可以说互信息:条件分布与边缘分布之间的KL散度的期望。
五. 一些补充
再看物理层安全与窃听信道模型的论文,碰到一些公式不太理解,于是乎在此做一些补充。大家其实可以直接跳到六总结。
如果我们将x看成信道的输入,y看成信道的输出,那么条件概率p(y|x)则代表信道转移概率。可以是Bob的信道,也可以是Eve的信道。那么我们可以写为:
备注:信道转移概率:当输入符号为 x时,信道输出符号 y的概率。
p(y)是Eve接收端的边缘分布,但是我们连输入x都没有,这该怎么表达呢?
答案就是遍历所有的输入,那么边缘分布可计算为:
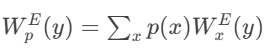
那么输入与输出的互信息则只与两个因素相关:一个是输入x的分布p(x),另一个是信道转移概率W,那么在信道编码理论中,可得:
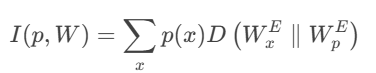
备注:信道编码(Channel Coding):在消息传输前,对信息进行冗余编码。在接收端,利用这些冗余信息,检测并纠正错误。
信道编码可以提高传输的可靠性。香农指出只要传输速率低于信道容量,就存在编码方式能使错误概率趋近于零。
六. 总结
互信息与KL散度的关系可以概括为:
-
互信息是联合分布与边缘分布乘积之间的KL散度。
-
互信息是条件分布与边缘分布之间的KL散度的期望。
在TIT期刊的论文经常使用KL散度的性质(如凸性和非负性)来推导互信息的界。






















 769
769

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










