详解密钥封装协议（KEM）

目录

一. 写在前面

二. 引入

三.密钥封装机制 

3.1 密钥生成算法

3.2 封装算法

3.3 解封装算法

3.4 小结

四. 混合加密

4.1 方案介绍

4.2 效率分析

4.3 参数实例化

五. 安全性分析

5.1 CPA安全

5.2 CCA安全

---

一. 写在前面

本文会用到的几个缩写：

KEM: key-encapsulation mechanism 密钥封装机制

DEM: data-encapsulation mechanism 数据封装机制

CPA: Chosen plaintext attack 选择性明文攻击安全

CCA: Chosen-Ciphertext Attack 选择性密文攻击安全

PPT: Probabilistic polynomial time 概率多项式时间算法

二. 引入

对于加密方案，名称上的一点说明：

公钥加密方案=非对称加密方案；

私钥加密方案=对称加密方案

在一般意义上，我们会认为私钥加密方案比公钥加密方案效率更高（不外加优化条件）。这是由于公钥加密方案会使密文扩张（ciphertext expanision）。

为了进一步优化算法，还可以将公钥加密方案与私钥加密方案进行级联，来形成混合加密方案（hybrid encryption）。如下图：

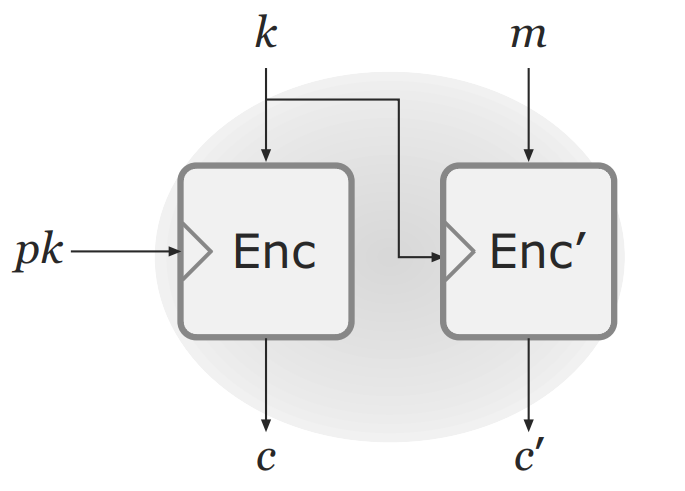
左边图：pk代表公钥，Enc代表公钥加密方案，k代表密钥，c是k的密文；

右边图：m是明文，Enc'是私钥加密方案，利用k对m进行加密形成c'；

在如上图的混合方案中，相当于利用公钥加密方案来形成共享密钥k，接着在私钥加密方案中，利用密钥k对明文m进行加密。

在接收端，利用非对称的私钥解密c得到公钥密钥k，接着使用k来解密恢复出原始信息m（message）。

由于发送端和接收端不需要提前共享密钥（secret key），所以这个方案其实更接近一个公钥加密方案（full-fledged public-key encryption）。

三.密钥封装机制 

在刚才的方案中，简单总结密钥k的作用：

（1）发送端一般均匀且随机的选取k

（2）发送端使用公钥加密方案来对k进行加密

那么这个过程其实就是密钥封装机制（key-encapsulation mechanism，KEM）。

与公钥加密方案类似，密钥封装机制也有三个PPT时间算法（Gen, Encaps, Decaps）。

3.1 密钥生成算法

Gen算法

输入：安全参数

输出：公私钥对(pk,sk）

一般认为n的具体取值由公钥pk决定（也就是由发送者决定）。通常情况下，公钥pk与私钥sk的比特长度都大于n。来看看官方表达：

3.2 封装算法

Encaps算法，总结为表达式：

输入：公钥pk

输出：密钥，对应的密文c。其中l(n)代表k的比特长度。

同时看看官方表达：

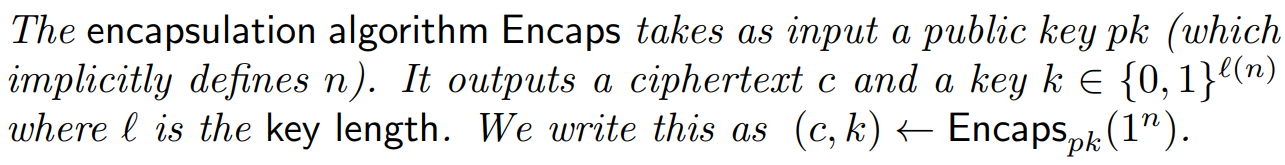
3.3 解封装算法

解封装算法Decaps是一个确定性算法，可总结为：

输入：私钥sk，密文c

输出：密钥k

需要注意的是，如果解封装失败的话，则会输出特殊的终止符号⊥。算法的官方表达：

3.4 小结

需要注意的是Gen算法与Encaps算法都具有随机性。

正确性要求:Encaps算法输出(c,k)，Decaps输入c，输出k。

在以上算法中，有的时候会做一点点修改，比如可以认为输出的密钥k是固定长度l的.

将公钥加密方案的明文，替换成一个随机的密钥k，也就是直观的KEM方案。

四. 混合加密

4.1 方案介绍

发送者调用Encaps算法来获得密文c以及密钥k。接着在私钥加密方案中，利用密钥k来加密明文m。

在这个过程中，私钥加密方案也可以看成数据封装机制（Data encapsulation mechanism, DEM）.

实际接收者可以得到两个密文c与c'，具体过程如下图：

在整个方案中涉及到两个解密私钥sk与k，具体的方案如下：

4.2 效率分析

现在，我们尝试回答一个问题：这样的混合加密其中包含了KEM，有什么好处吗？

首先固定k的比特长度为n。

假定密钥封装后的c的长度为，那么可以认为密钥封装的开销（cost）为。

对于私钥加密方案Enc'的每比特明文所生成的密文长度为，也就是cost per bit of plaintext。在私钥加密方案中可认为明文的长度大于密钥k的长度，也就是|m|>n（这样效率更高）。

在混合加密方案中，每比特明文所对应的密文长度有两部分c与c'，由此可计算为：

可以观察到，当m的长度足够大时，该值趋近于。换句话说，当明文长度足够大时，混合加密的开销与私钥加密的开销一致。那么，混合加密方案虽然披着公钥加密的框架，但是效率却可以接近私钥加密方案，这是混合加密方案的优势之一。

4.3 参数实例化

假定密钥k的长度为n，密文c的长度为L，密文c'的长度为n+|m|。那么，在混合加密方案中，密文总长度为：

如果我们直接使用公钥加密方案会怎么样？

加密n比特的消息，假定密文长度为L。

按照线性比列关系，加密|m|比特长度的消息，密文长度为：

考虑明文长度|m|足够大时，混合加密可以提升极大地效率。

举一个简单的例子。假定密钥k的长度n=128-bite。假设公钥加密之后的c的长度为256-bit。如果使用基础的公钥加密方案，当消息为1MB时，密文则为2MB。

接下来我们计算使用KEM的混合加密方案的效率。跟刚才一样，利用β代表私钥加密方案的每比特计算量，可以假设：

利用之前的公式，当消息为1MB时，混合加密的计算消耗为：

原始的公钥加密方案计算消耗为：

那么很明显计算效率提升16倍，密文长度优化了2倍。

备注：以上计算中使用到了

五. 安全性分析

很显然，混合加密方案的安全性依赖于密钥封装机制与私钥加密方案的安全性。此处可简单给出两个密钥封装协议的CPA与CCA安全。

5.1 CPA安全

假定KEM是CPA安全的，私钥加密方案符合基本的安全性，那么混合加密方案则也是CPA安全的。

实际上，我们可以感受到密钥封装协议可以保证密钥k的安全，且足够随机，每次加密k只使用一次，所以只要KEM满足CPA安全即可。

进一步，可以将KEM方案看成一个伪随机生成器（pseudorandom generator），那么则可以形成流密码。

5.2 CCA安全

假定KEM是CCA安全的，私钥加密方案也是CCA安全，那么混合加密方案则也是CCA安全的。