即使我们有着高精度的相机,我们得到的数据通常是受各种未知噪声影响的,运动方程和观测方程也只能近似的成立,因此需要研究如何在有噪声的数据中进行准确的状态估计。
1、状态估计问题
1.1、最大后验与最大似然
经典 SLAM 模型由一个运动方程和一个观测方程构成
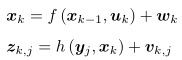
其中表示相机位姿,
表示传感器输入,
表示观测数据,
表示路标,
和
表示噪声,一般认为噪声服从零均值高斯分布
~
,
~
运动方程在视觉 SLAM 中没有特殊性,一般讨论观测方程。对于观测方程,希望通过带噪声的数据和
,推断位姿
和地图
(以及它们的概率分布),这构成了一个状态估计问题。主要的解决思路是使用滤波器、非线性优化
滤波器关心当前时刻的状态估计,而对之前的状态则不多考虑;而非线性优化使用所有时刻采集到的数据进行状态估计,一般认为优于滤波器
在非线性优化中,将待估计变量放入一个状态变量 中
对机器人进行状态估计,也就是求已知输入和观测
的条件下,状态
的条件概率分布
特别地,当我们没有测量运动的传感器,只有一张张的图像时,即只考虑观测方程带来的数据时,相当于估计 的条件概率分布。如果忽略图像在时间上的联系,把它们看作一堆彼此没有关系的图片,该问题也称为SfM,即如何从许多图像中重建三维空间结构,SLAM 可以看作是图像具有时间先后顺序的,需要实时求解一个 SfM 问题
利用贝叶斯法则估计状态变量的条件分布 ,其中左侧是后验概率,
是似然,
是先验
直接求后验分布是困难的,但是求一个状态最优估计,使得在该状态下,后验概率最大化(Maximize a Posterior,MAP),则是可行的
,
与待估计的状态
无关,因而可以忽略
上式说明,求解最大后验概率,相当于最大化似然和先验的乘积;进一步,如果我们不知道机器人的位姿(没有先验),则可以求状态的最大似然估计(Maximize Likelihood Estimation, MLE)
似然是指“在现在的位姿下,可能产生怎样的观测数据”。由于我们知道观测数据,所以最大似然估计,可以理解成:“在什么样的状态下,最可能产生现在观测到的数据”
1.2、最小二乘法
利用最小二乘法可以求解最大似然估计。对于某一次观测
![]()
假设噪声服从零均值高斯分布 ∼
,因此观测数据的条件概率也服从高斯分布





 本文探讨了在视觉SLAM中如何通过最大后验与最大似然方法,结合滤波器和非线性优化技术,处理受噪声影响的相机数据,以实现精确状态估计。重点介绍了最小二乘法在最大似然估计中的应用,以及高斯牛顿法和列文伯格—马夸尔特法在求解非线性最小二乘问题中的策略。
本文探讨了在视觉SLAM中如何通过最大后验与最大似然方法,结合滤波器和非线性优化技术,处理受噪声影响的相机数据,以实现精确状态估计。重点介绍了最小二乘法在最大似然估计中的应用,以及高斯牛顿法和列文伯格—马夸尔特法在求解非线性最小二乘问题中的策略。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 4195
4195

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








