视觉SLAM理论入门——（7）视觉里程计之特征点法—对极几何

最新推荐文章于 2025-10-10 23:45:00 发布

原创

最新推荐文章于 2025-10-10 23:45:00 发布 · 1.4k 阅读

·

1

·

CC 4.0 BY-SA版权

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

文章标签：

本文介绍了如何通过ORB特征匹配估计单目和双目的相机运动，包括对极约束、本质矩阵的求解方法，以及单应矩阵的计算和应用。重点讲解了对极几何的原理、本质矩阵的内在性质和求解过程，以及如何结合深度信息进行三角测量来估计点的三维位置。

提取ORB特征后，需要根据点估计相机的运动。根据相机的原理，可以分为下面几种情况：

1、当采用单目相机，只知道2D像素坐标，需要根据两组2D点估计运动，这时用对极几何求解

2、当采用双目相机、RGB-D相机，或者通过其他方法知道距离信息，需要根据两组3D点估计运动，这时用ICP求解

3、如果是一组3D点、一组2D点（也就是得到了一些3D点和它们在相机的投影位置），这时用PnP求解

1、对极约束

当希望求取两帧图像 $I_1, I_2$ 之间的运动，设第一帧到第二帧的运动为 $R,t$ 。两个相机中心分别为 $O_1, O_2$ 。现在，考虑 $I_1$ 中有一个特征点 $p_1$ ，它在 $I_2$ 中对应着特征点 $p_2$ 。这两个点是通过特征匹配得到的。如果匹配正确，说明它们确实是同一个空间点在两个成像平面上的投影

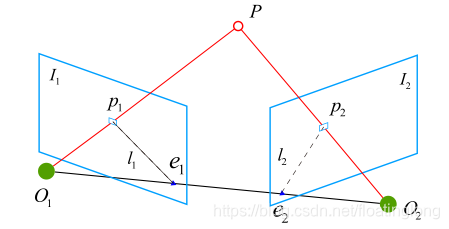
为了描述它们之间的几何关系，用到了极平面、极点、基线、极线等概念

极平面： $O_1,O_2,P$ 所在的平面

极点： $O_1, O_2$ 连线与像平面 $I_1, I_2$ 的交点 $e_1,e_2$

基线： $O_1, O_2$ 连线

极线：极平面与两个像平面 $I_1, I_2$ 之间的相交线

从第一帧的角度上看，射线 $\underset{O_1p_1}{\rightarrow}$ 是某个像素 P 可能出现的空间位置，如果不知道 P 的位置，那么当我们在第二个图像上看时，极线 $e_2p_2$ 是 P 可能出现的投影位置，也是射线 $\underset{O_1p_1}{\rightarrow}$ 在第二个相机中的投影。当我们通过特征点匹配，确定了 $p_2$ 的像素位置，从而能够推断 P 的空间位置以及相机运动

设 $P = [X,Y,Z]^T$ ， $s_1 p_1 = KP$ ， $s_2 p_2 = K(RP+t)$ （R,t描述第一个坐标系到第二个坐标系的运动）

最低0.47元/天解锁文章

评论

成就一亿技术人!

拼手气红包6.0元

还能输入1000个字符

添加红包

插入表情

表情包

代码片

HTML/XML
objective-c
Ruby
PHP
C
C++
JavaScript
Python
Java
CSS
SQL
其它

条评论被折叠查看

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。