假设有一组配对好的 3D 点
![]()
想要找一个欧氏变换 R,t,使得:
![]()
这个问题可以用迭代最近点(Iterative Closest Point, ICP)求解。ICP求解方法有两种方法:线性代数求解(SVD)、非线性优化求解
1、线性代数求解法
定义第 i 对点的误差为
![]()
定义两组点的质心:

构建最小二乘问题,求使误差平方和达到极小的 R,t:
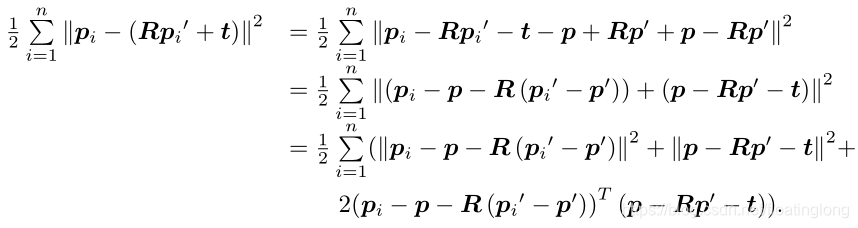
 该文详细介绍了如何通过线性代数和非线性优化方法解决3D点集配对的欧氏变换问题。线性代数方法利用最小二乘原理和奇异值分解(SVD)估计旋转矩阵R和平移向量t;非线性优化方法则涉及李代数和雅可比矩阵,寻找误差函数的极小值。文中还讨论了ICP问题可能存在的唯一解或无穷多解的情况。
该文详细介绍了如何通过线性代数和非线性优化方法解决3D点集配对的欧氏变换问题。线性代数方法利用最小二乘原理和奇异值分解(SVD)估计旋转矩阵R和平移向量t;非线性优化方法则涉及李代数和雅可比矩阵,寻找误差函数的极小值。文中还讨论了ICP问题可能存在的唯一解或无穷多解的情况。
假设有一组配对好的 3D 点
![]()
想要找一个欧氏变换 R,t,使得:
![]()
这个问题可以用迭代最近点(Iterative Closest Point, ICP)求解。ICP求解方法有两种方法:线性代数求解(SVD)、非线性优化求解
定义第 i 对点的误差为
![]()
定义两组点的质心:

构建最小二乘问题,求使误差平方和达到极小的 R,t:
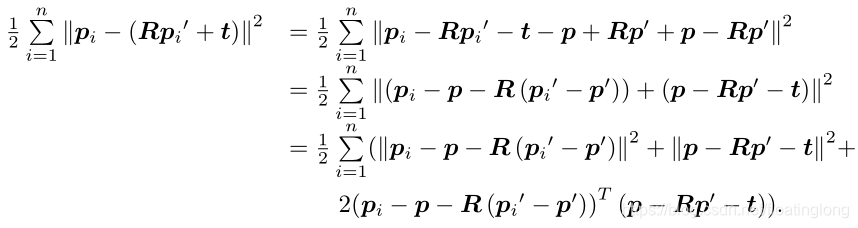
 3037
3037
 1203
1203
 3587
3587

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


