求对着目标物体环绕拍摄的相机参数lookAt

原创已于 2022-10-01 18:06:25 修改 · 1.3k 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#计算机视觉 #图像处理 #算法

于 2022-10-01 17:37:50 首次发布

本文探讨了两种实现环绕拍摄的方法：欧拉角旋转与lookat方案，并详细解析了lookat方案的具体实现步骤及代码示例。

求对着目标物体环绕拍摄的相机参数lookAt

求对着目标物体环绕拍摄的相机参数lookAt

目标

在物方原点处存在一个目标，我们希望获得围绕目标的“观看”的相机pose，从而渲染目标
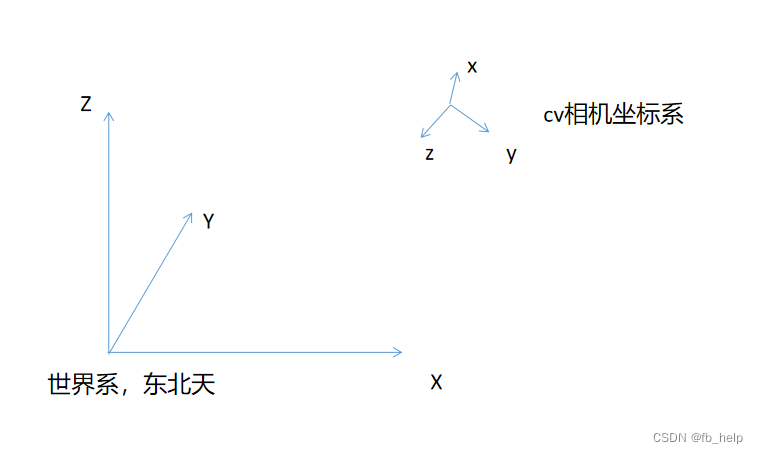
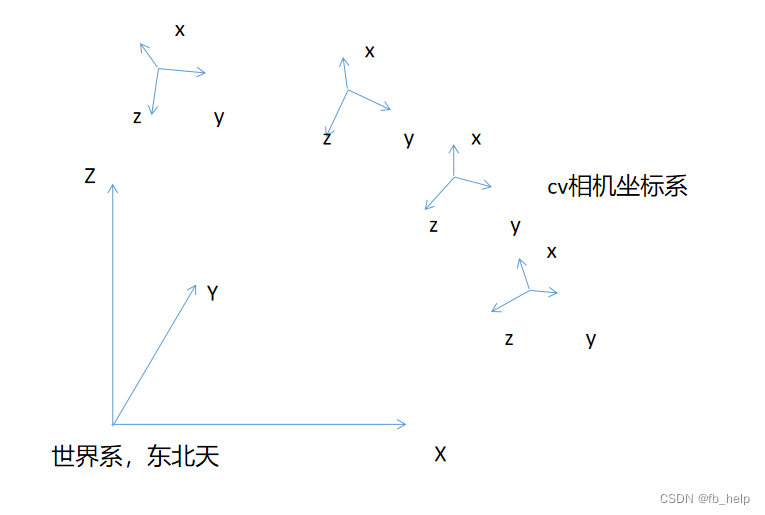
在这里插入图片描述

第一个想法：旋转坐标系（欧拉角旋转）

目标是将世界系变换到相机系

通过旋转世界坐标系，让它变到相机坐标系，记录下该过程的变换矩阵M。

我的想法：
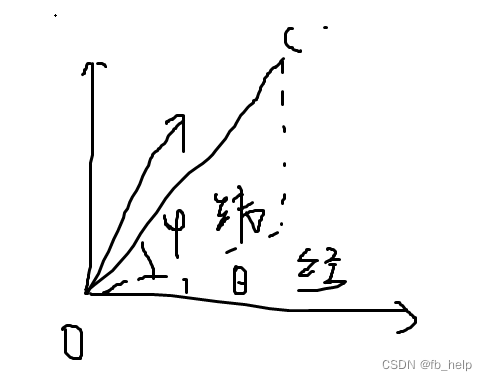
在这里插入图片描述

相机原点的经纬度可以通过角度计算出来，将世界系（0,0,1）根据经纬度的计算的欧拉角对坐标系进行旋转变换

最终这个方案失败了
有几点我没弄清楚：

这个旋转过程是需要内旋还是外旋
这个旋转过程需要旋转哪些轴，以及哪些轴需要旋转多少度（实验中是先旋转Z轴经度，再旋转y轴纬度）
每一次旋转记录的旋转矩阵到底是world2camera还是camer2world
欧拉角的24种旋转方法搞不懂
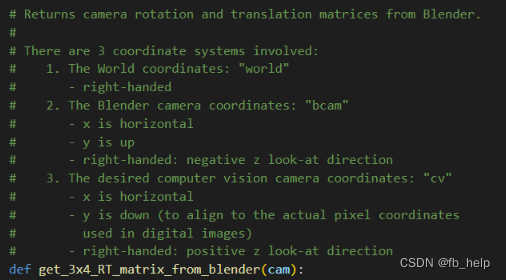
欧拉角广泛应用于图像学的渲染领域，参考opengl的教程得到的是图形学的相机，最后还需要转换到cv相机（与cv相机z朝外，y朝下不同，图像学相机z朝里，y朝上）（它们之间的转换见下图）
这个过程中的耦合度太高，不宜检查出出错的地方。

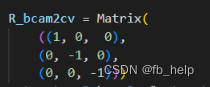
因此，这种方案我放弃了，改用了lookat方案

第二个想法：lookat方案（或者称为矩阵分析方案）

环绕拍摄有一个特点，相机一定朝向原点。我们基于这个约束可以对矩阵进行分析，最终求得需要的变换矩阵。

重点 矩阵分析：

对于world2camera的变换矩阵M（4*4）它满足这些条件：对于相机坐标系的o_cam（0,0，0,1）,M@o_cam
=M[:3,3] = 相机在世界系下的坐标。对于相机坐标系的Z轴（0,0，1，1） M@Z = M[:3,2] = 相机Z轴在世界系下的方向向量。（对于lookat来说，就是相机原点到物方原点的单位向量）对于相机坐标系的X轴（1,0，0，1）
M@X = M[:3,0] =
相机X轴在世界系下的方向向量。（对于环绕拍摄来说，x轴一定在x0y平面上，且其t在x0y上的投影与x轴的夹角为经度+90）
对于相机坐标系的Y轴（1,0，0，1） M@Y = M[:3,1] 由于XYZ三轴垂直，因此Y = coss(Z,X) 注意这里是右手系，Z到X才为Y轴

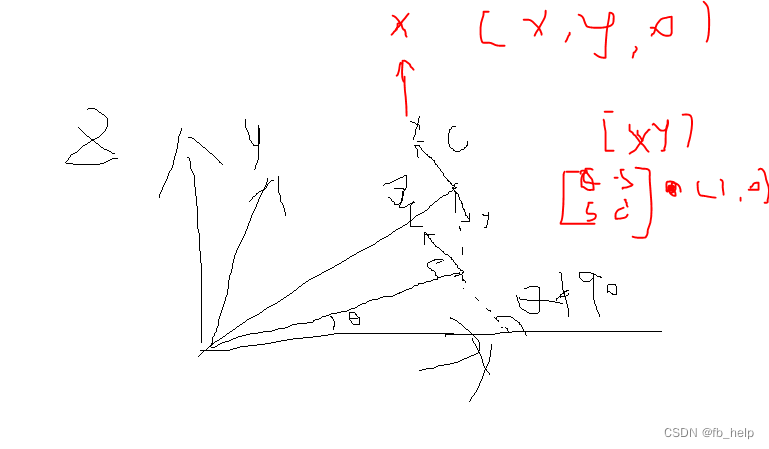
在这里插入图片描述
我们发现经过矩阵分析后，矩阵M的前三行都可以根据实际Z轴和X轴的朝向而计算出来。
我们的变换矩阵被填充完了。即完成了变换。最终获得camera2world的变化矩阵M

代码：

def pose_look_at_q(jingdu, weidu, radius): #经度纬度半径
    # 计算相机Z轴在世界系下向量的坐标

    jingdu = jingdu/180.*np.pi
    weidu = weidu/180.*np.pi

    x = radius*math.sin(weidu)*math.cos(jingdu)
    y = radius*math.sin(weidu)*math.sin(jingdu)
    z = radius*math.cos(weidu)

    Z = -np.array([x,y,z]) #注意这里要取负号，相机z轴在世界系下的方向向量，是C到O

    # 计算相机X轴在世界系下向量坐标
    x_world_2d_ori = np.array([1,0])
    jingdu_X = jingdu+0.5*np.pi
    transform = np.array([
        [np.cos(jingdu_X),-np.sin(jingdu_X)],
        [np.sin(jingdu_X), np.cos(jingdu_X)]
    ])
    x_world_2d_cam = transform@x_world_2d_ori
    X = np.array([x_world_2d_cam[0],x_world_2d_cam[1],0])  #这里乘的顺序
    
    # 计算相机Y轴在世界系下坐标  叉乘的顺序
    Z = Z/ np.linalg.norm(Z) #归一化

    Y = np.cross(Z,X) #叉乘的顺序,右手法则
    #print(np.linalg.norm(Z))
    #print(np.linalg.norm(X))
    #print(np.linalg.norm(Y))
    Y = Y/ np.linalg.norm(Y)
    #print(np.array([x,y,z])+Y)

    # c2W 
    P = np.array([
        [1,0,0,0],
        [0,1,0,0],
        [0,0,1,0],
        [0,0,0,1.]])
    P[:3,0] = X
    P[:3,1] = Y
    P[:3,2] = Z
    P[:3,3] = [x,y,z]

    P = torch.Tensor(np.array([[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]])) @ P
    return P
render_poses = torch.stack([pose_look_at_q(angle, 30, 1) for angle in np.linspace(0,360,25)[:-1]], 0)

举一反三

如果并不想对着原点环绕拍摄，而是想对着[x,y,z]环绕拍摄。
那么先按照上述方法对着原点拍摄，即 camera2ori, 再 ori2obj。则M（camera2obj）= M（camera2ori）*M（ori2obj）

一些其它材料

pose 对不对的检查方法

如果w2c的矩阵最后一列不是0,0，r就是错误的，因为位置一般都是对的，如果再相机主光轴朝向原点，那姿态也对了

w2c的最后一列是不是0，0，R
c2w的最后一列是不是相机中心在世界系下坐标即C

在这里插入图片描述
https://blog.youkuaiyun.com/xinxiangwangzhi_/article/details/124650910

旋转的方法的一个问题：乘以了一个矩阵后，不知道是向量变化了还是基底变化了。

https://blog.youkuaiyun.com/weixin_45632220/article/details/117735223?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522166459883816782425196130%2522%252C%2522scm%2522%253A%252220140713.130102334…%2522%257D&request_id=166459883816782425196130&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2_alltop_positive~default-1-117735223-null-null.142^v51control,201^v3control_1&utm_term=%E6%97%8B%E8%BD%AC%E7%9F%A9%E9%98%B5&spm=1018.2226.3001.4187