约束优化问题
权重衰退

这里是一个不等式约束
回顾等式约束的处理方法:
sub (wi = xi)
min l(w,b) + (wi - xi)2
为了让能量函数最小,wi要靠近xi,这是等式约束,
对于不等式约束:

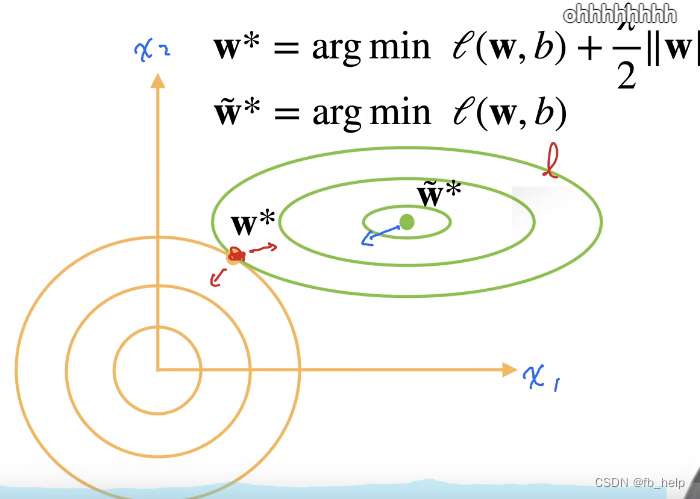
对于不等式约束,我们通过权重来实现软约束。
为了让能量函数最小,||W||2要尽量小。,这里为什么没有出现sigma。
原因是:让||W||2小,也就是让||W||2小于sigma,它们是等价的。sigma为任何值都是让||W||2小,||W||2不需要像等式约束那样接近sigma。
控制||W||2重要性的指标是它前面的权重。
目标函数关于第二项的导数恒为lamdaW,即每次迭代w都会衰减,第一项需要w优化到真值,两者通过lamda平衡
当第一项解决真值时,其相关梯度会变小,梯度会更考虑正则化项项。反之,过于考虑正则化项后,数据项梯度又会增大,会考虑数据项(第一项)最终形成平衡
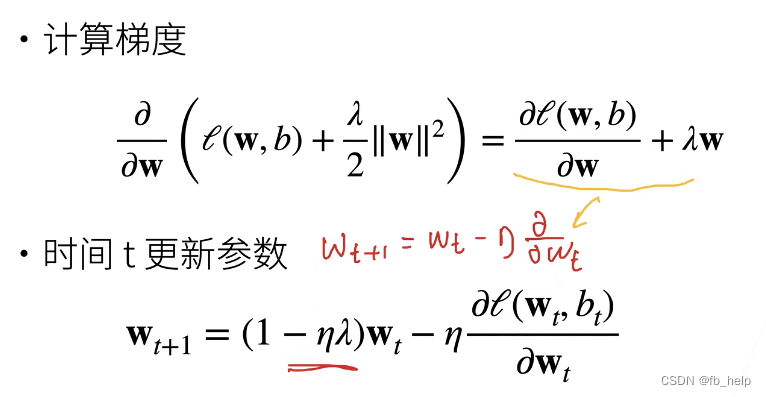




 本文探讨了约束优化问题,重点在于权重衰退在处理不等式约束中的作用。通过让能量函数最小化,权重向量的范数被控制以满足软约束。权重衰退使得在优化目标和正则化项之间达到平衡,当数据项优化接近真值时,正则化项开始起主导作用,反之亦然,从而在训练过程中找到一个合适的平衡点。
本文探讨了约束优化问题,重点在于权重衰退在处理不等式约束中的作用。通过让能量函数最小化,权重向量的范数被控制以满足软约束。权重衰退使得在优化目标和正则化项之间达到平衡,当数据项优化接近真值时,正则化项开始起主导作用,反之亦然,从而在训练过程中找到一个合适的平衡点。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








