softmax回归详解

softmax回归

softmax回归

相较与线性回归softmax回归的输出有多个，适用于多分类问题。

softmax的估计值

线性回归的估计值是y_hat，只有一个一维值（这个值的范围有时归一到0~1，线性函数的输出不一定是0 ~ 1），而softmax回归的输出有多维，那么它的估计值应该也是一个同维数向量，仿照线性回归，我们可以将这个向量每个值先进行exp（x）运算，再归一化：

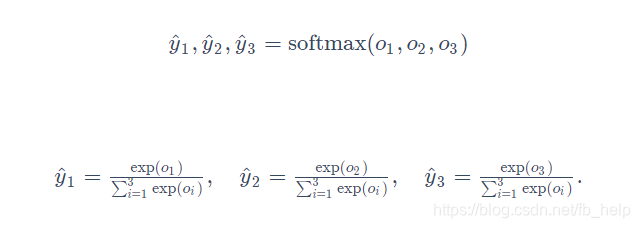
这样就将一个输出向量变成了一个概率分布，即该输出向量即估计向量，表达了其属于每一类的概率，且所有维之和为1，这样符合我们想要的假设：针对一个输入向量，我们计算出了它属于每一类的概率，且所有类概率和为1（只能属于这几类）。

softmax的损失函数

线性回归的损失函数衡量的是估计值与真值的差（或称相似度），而softmax输出的估计值，是归一化的向量，其中每一维值表示该输入属于每一维的概率。而对于真值来讲，按照softmax估计值的形式真值应为【1,0,0,0】或【0,0,1,0】这种形式，因为这种向量形式表达了属于某一类的概率为1，其它类的概率为0。
损失函数描述的是估计值与真值之间的差（或相似性），对于softmax来说，真值和估计值为同维的向量，可以将线性回归的平方差损失函数用在此处，让两个向量做差求模平方。但相比于平方差损失函数，softmax的损失函数更好的是交叉熵损失函数:

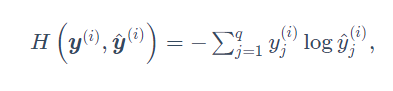
交叉熵损失函数计算的是量向量之间的熵或者称相似性，如果两向量更相似也说明了两向量的损失小。

使用交叉熵损失函数的另一个原因是，我们希望衡量两个向量的趋势，即在某一类概率远大于其他类即可。没有必要让这个特征只能是某一类而其他类是0（这与我们日常生活也是相符的，小猫与小狗有很多相似特征，我们对他们的识别概率不能一定是1或0）