NCC归一化互相关(详解)

NCC归一化互相关(详解)

NCC是什么

NCC（Normalized cross-correlation）是模板匹配中较为常见的互相关计算方法。
来描述两个同维向量，窗口或样本之间的相关性。其取值范围是-1~1，-1代表两向量不相关，1代表两向量相关

应用

NCC常做作为相似性的度量。当NCC为-1时，两向量负相关（你东我就西），当NCC为0时，两向量不相关（你东我随意），当NCC为1时，两向量正相关（你东我就东）。因此，NCC值越大，两向量越相似。反正不相似。

NCC的计算公式

NCC的计算公式网上有多种：

1. https://blog.youkuaiyun.com/weixin_42104289/article/details/83088043
   
2. https://blog.youkuaiyun.com/jia20003/article/details/53021614
3. https://blog.youkuaiyun.com/qq_32261049/article/details/78666654
   
4. NCC

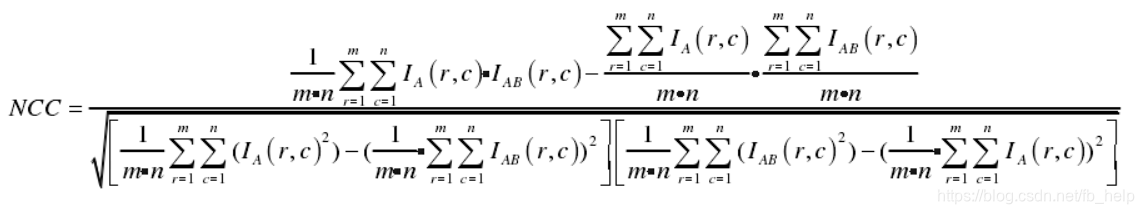
这些结果存在问题：

第一NCC这个叫法是有歧义的，特别是图像模板匹配领域的人，对NCC和ZNCC有区分，详情见 NCC与ZNCC。由于其存在多义性，本篇所说的NCC，以公式为其标识。

简约的计算公式

网上多数结果过于复杂，不好理解，简便而优美的公式见：

其中，f(),t(),为两个向量或样本，n为向量维数或窗口的大小，σ为各种样本的标准差，μ为各自样本的均值。

理解

NCC与相关系数

不难发现，NCC的计算公式与相关系数的计算公式一致，及：

相关系数就更好理解了，描述两样本的相关性，其实NCC就是计算两影像窗口内像素的相关系数。

NCC与向量夹角

另外NCC可以看作两个影像窗口内各像素组成的向量之间的夹角。详情见 NCC与ZNCC。