使用频率扫描微波传输的新密度无关湿度测量方法

1 引言

有机材料的含水量对其加工技术具有显著影响。定义如下：

$\psi = \frac{m_w}{m_w + m_d} \cdot 100\%$

其中， $m_w$ 和 $m_d$ 分别表示水分和干物质的质量。通常，通过干重法来测定含水量，但这种方法既费时又繁琐。然而，微波技术在这一方面的应用相比其他非接触测量方法（如辐射测量或红外设备）显示出许多优势。

微波能够穿透显著的深度，因此能够提供材料整体的平均含水量。衰减（以Np为单位）和相移（以弧度为单位）可分别表示为：

$\frac{\omega}{c} \cdot L \cdot R(\rho) \cdot g_1(\varepsilon_r(\psi))$

和

$\Phi = \frac{\omega}{c} \cdot L \cdot R(\rho) \cdot g_2(\varepsilon_r(\psi))$

其中，材料层相对于自由空间的衰减和相移与含水量相关，这通过复介电常数 $εr=ε′−jε′′\varepsilon_r = \varepsilon' - j\varepsilon''$ 表示。

但也依赖于密度 $ρ\rho$ （ $ω\omega$ 为角频率， $c$ 为真空中光速）。实验发现， $A$ 和 $Φ\Phi$ 显示出几乎相同的密度函数依赖性 $R(ρ)R(\rho)$ ，而 $g_1$ 和 $g_2$ 是复介电常数（从而也是含水量）的不同函数。

2 密度无关的含水量测量

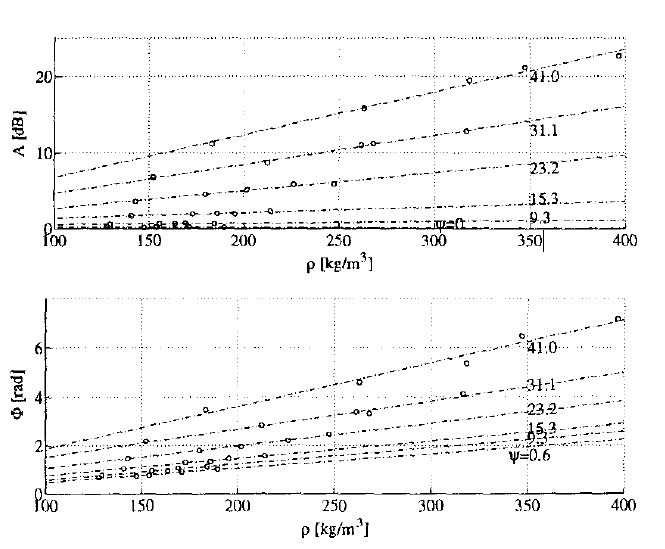
图1：不同烟草的含水量 $ψ\psi$ 值下的衰减和相位随密度的变化（10GHz）

仅使用微波的两参数测量中，密度无关的微波含水量测量最早由 [1] 于1977年提出，之后于1980年由 [2] 进一步发展。对 [1] 的进一步改进见 [3, 4]。根据 [1]，密度的依赖性被假定为 $R(ρ)=ρR(\rho) = \rho$ ，从而得到

$\frac{A}{\rho L} = M_1(\psi) \quad \text{和} \quad \frac{\Phi}{\rho L} = M_2(\psi) \quad (4)$

$M_1$ 和 $M_2$ 是与含水量有关的函数，而不依赖于密度。对 $ρ\rho$ 的线性依赖关系通常满足。

正如图1中对烟草的例子所示，这种情况并不总是成立。通过结合方程 (4)，关系

$X_1 = \frac{A}{\Phi} = M(\psi) \quad (5)$

仅是含水量的函数。在实际应用中，需要对具有不同含水量的材料进行 $A$ 和 $Φ\Phi$ 的校准测量。此外， $(ρL)(\rho L)$ 产品需要通过实验测定。然后， $M_1$ 和 $M_2$ 可以通过适当选择的函数进行数值拟合。最终， $M(ψ)M(\psi)$ 可以被计算，并在某些情况下通过解析方法求逆，以得出

$\psi = M^{-1} \left( \frac{A}{\Phi} \right) \quad (6)$

按照文献 [3] 的方法，密度无关的

$X_2 = \frac{\varepsilon'(\psi, \rho) - 1}{\varepsilon''(\psi, \rho)} \quad (7)$

被提出并通过实验测量进行了验证。然而， $εr\varepsilon_r$ 只能在已知 $L$ 的情况下通过传输测量确定，这种情况较为少见。因此，[3] 中指出，当 $ε′\varepsilon'$ 和 $ε′′\varepsilon''$ 取低值时， $X_2$ 可以通过以下方式近似：

$X_2(\psi) \propto \frac{\Phi(\psi, \rho)}{A(\psi, \rho)} \quad (8)$

这是一个与 $L$ 和 $ρ\rho$ 无关的函数。在实践中，对于给定的材料，含水量 $ψ\psi$ 是可变的。在固定的含水量和给定的密度下，将 $A$ 和 $Φ\Phi$ 的测量值映射在 $Φ\Phi$ - $A$ 图中。该图中的第二个点是原点，然后通过两个点定义一条直线。假设含水量与该曲线的斜率成比例。

从 [5] 中可以推导出该过程的进一步改进，[5] 通过改变密度或层厚 $L$ 来绘制 $Φ\Phi$ - $A$ 图，以确定给定的 $ψ\psi$ 。

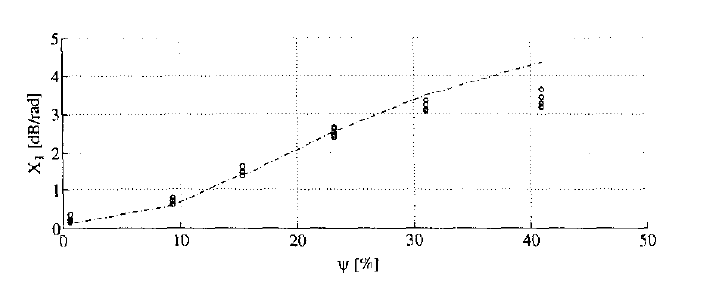
图2：烟草的含水量 $X_1$ 与校准曲线及测量值的关系（10GHz）

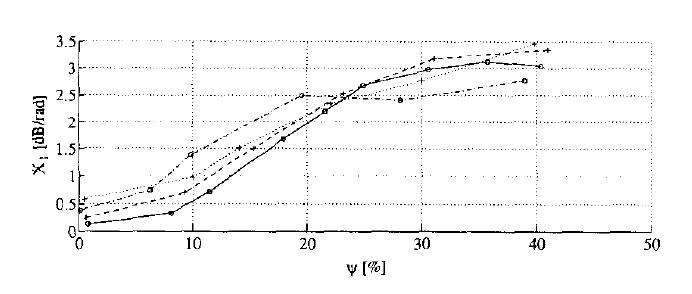
图3：测量的 $X_1$ 与含水量的关系，适用于油菜籽（- ·）、燕麦（··）、烟草（- -）和墨角兰（-）（10GHz）

从一组测量点中得到的直线斜率代替了仅使用一个测量点和原点的情况。

为了进一步说明所描述的密度无关含水量测定方法，基于烟草的测量给出了一些实验结果。根据 [1]，通过对图1中的 $A$ 和 $Φ\Phi$ 的测量点进行直线插值，可以绘制出 $ρ=常数\rho = \text{常数}$ 的曲线，作为 $ψ\psi$ 的函数。生成的点通过抛物线函数拟合：

$\frac{A}{\rho L} = a \cdot \psi^2 + b \psi + c \quad (9)$

和

$\frac{\Phi}{\rho L} = d \cdot \psi^2 + e \psi + f \quad (10)$

得到一个校准曲线

$X_1 = \frac{a \psi^2 + b \psi + c}{d \psi^2 + e \psi + f} \quad (11)$

通过反转该公式，可以得到 $ψ(X1)\psi(X_1)$ 。

这种依赖关系在图2中有所描述，并显示了来自 [3] 的测量点。可以看出，两种方法在含水量 $ψ≈8−25%\psi \approx 8-25\%$ 之间效果很好。得到了一条S形的校准曲线。对于许多其他有机材料（例如油菜籽、燕麦和墨角兰），也可以观察到类似的结果，如图3所示。

对于较低的 $ψ\psi$ 值，水分与材料紧密结合。衰减和相移随 $ψ\psi$ 的增加缓慢上升。大约在10%到25%之间，衰减的增加速度快于相位，且测量过程效果良好。对于较高的含水量，只有自由水增加， $A$ 和 $Φ\Phi$ 的行为相似。这意味着校准曲线变平甚至可能失去唯一性。在 $A$ 和 $Φ\Phi$ 中的微小测量误差会导致关联的 $ψ\psi$ 值出现较大偏差，使整个测量方法变得不切实际。

总结已建立的密度无关的含水量测量方法的特点，可以做出以下声明：

各种方法效果相当好，因为它们基于比值 $AΦ\frac{A}{\Phi}$ ；
校准需要大量的工作，因为对于恒定的含水量 $ψ\psi$ ，需要改变层厚和/或密度；
这些方法仅在有限的含水量范围内效果良好。

本论文的目的是引入新的密度无关测量方法，这些方法极大地简化了校准过程，并且在高达40%甚至更高的含水量下也能正常工作。通过适当选择操作参数，可以避免在高含水量时校准曲线的变平。因此，由于曲线斜率更陡，测量精度得到了极大提高。关于校准，不需要实验室参考测量，也不需要层厚或密度变化，从而实现用户使用测试材料进行现场校准。

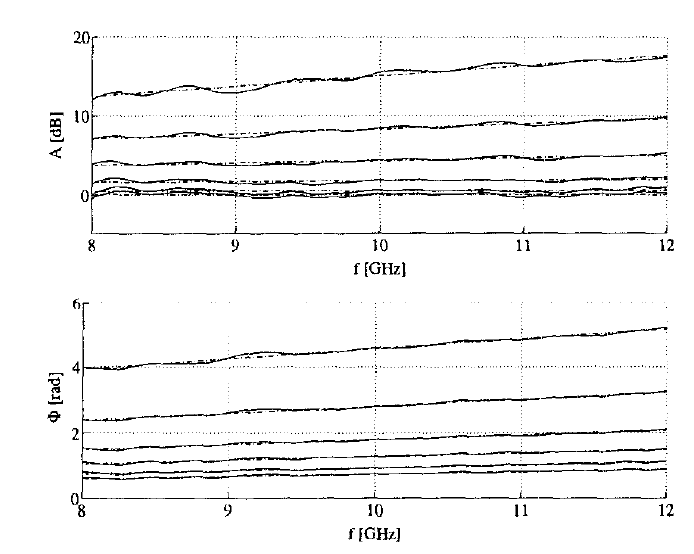
图4：不同含水量的烟草在不同频率下的衰减和相移

3 新方法

新的测量方法基于在宽频率范围内的衰减和相位测量。使用频率扫描数据并不是新方法，但之前仅用于插值，以提高特定频率下的精度，然后在进一步计算中使用。在新的方法中，记录并评估了 $A$ 和 $Φ\Phi$ 随频率的变化。

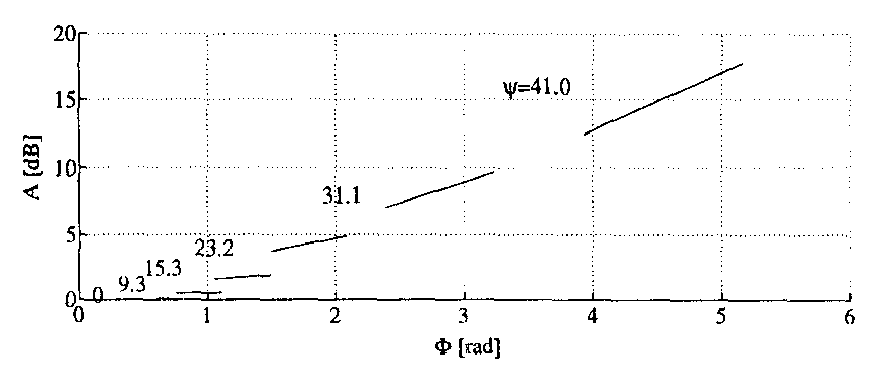
图5：不同含水量下烟草的衰减与相移关系

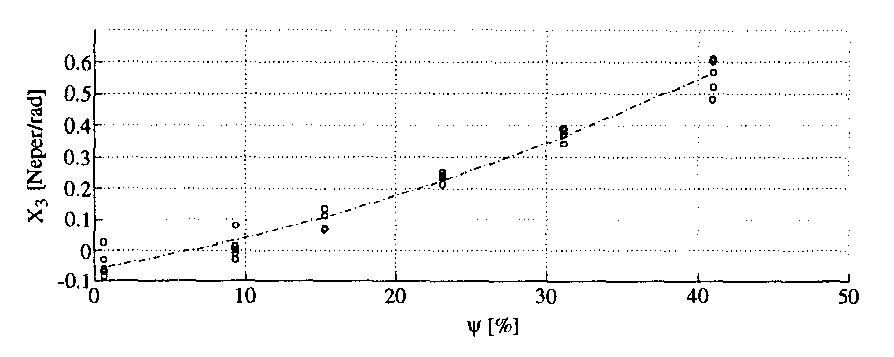
图6：不同密度下烟草的 $A−ΦA-\Phi$ 图的斜率与含水量的关系

通过这种方法，作为第一个新特性，在线校准过程得以实现。观察方程 (2) 和 (3) 显示，只要 $εr\varepsilon_r$ 近似恒定，频率变化就会像层厚和密度一样改变幅度和相位。对于低于 3 GHz 的微波频率，这是适用的情况，此时水的 $ε′\varepsilon'$ 几乎恒定，并且从离子导电到偶极弛豫损耗的过渡使得 $ε′′\varepsilon''$ 在很大程度上保持频率无关性。将 $A$ 与 $Φ\Phi$ 作图有助于获取直线的斜率，这是一种密度无关的含水量测量方法。随着频率的增加， $εr\varepsilon_r$ 的色散增大，从而导致 $g_1$ 和 $g_2$ 依赖于频率。然而， $A/ΦA/\Phi$ 的比值依然是密度无关的，并且是含水量的函数。该函数的斜率虽然通常不同于之前解的斜率（5）或（8），但仍然可以作为含水量的测量值。

新的测量方法在X波段（8-12 GHz）通过烟草的测量结果进行了说明。如图5所示，衰减 $A$ 和相移 $Φ\Phi$ 依然几乎线性地依赖于频率，尽管自由水的介电常数在使用的频率范围内显示出显著色散 [6]。直线斜率随含水量 $ψ\psi$ 的增加而随频率增大。因此，绘制 $A−ΦA-\Phi$ 图再次得出直线，这与之前的方法相同。

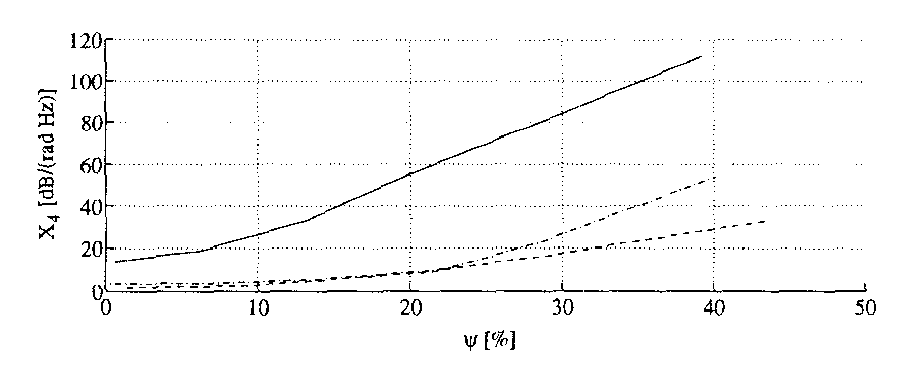
图7：不同含水量下烟草（- -）、墨角兰（- ）和油菜籽（-）的 $X_4$ 值

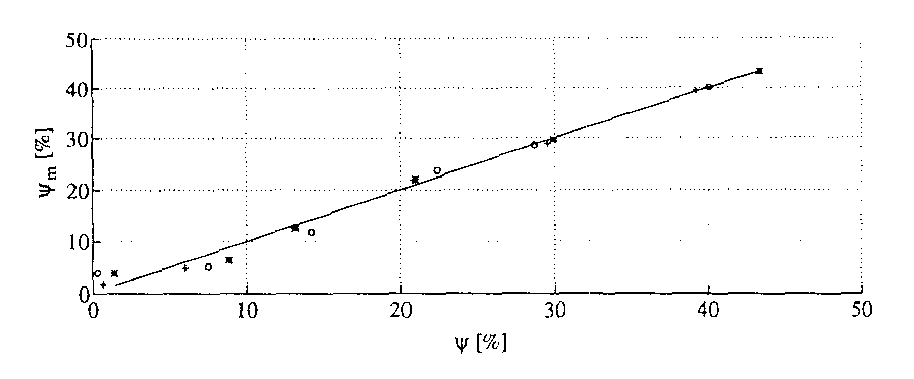
图8：测量的含水量 ( $X_4$ ) 与烟草 (o)、墨角兰 (★) 和油菜籽 (+) 的含水量的关系

图6显示了一个校准曲线：

$X_3 = \frac{\Delta A(\omega) / \Delta \omega}{\Delta \Phi(\omega) / \Delta \omega} \propto \frac{\Delta g_1(\varepsilon_r(\omega))}{\Delta g_2(\varepsilon_r(\omega))} \quad (12)$

与先前的曲线（图2和图3）相比，可以看到一个显著的改进。该函数的斜率变得平滑，且高含水量处的平坦现象完全消失。这是由于频率范围的选择，即 $εr\varepsilon_r$ 的色散导致的。通过调整频率范围来针对 $ε′\varepsilon'$ 和 $ε′′\varepsilon''$ 的色散，可以获得不同的函数依赖关系，这取决于所测量的材料。在实际应用中，可以使用适当的函数（多项式或指数曲线）来拟合校准曲线，并通过直接反演获得测量值与含水量之间的关系：

$\psi = f(X_3) \quad \text{例如, } \psi = k_1 X_3^2 + k_2 X_3 + k_3 \quad (13)$

根据 (12) 进行评估并不是唯一的可能性，还可以使用其他函数。计算比值

$X_4 = \frac{d}{d\omega} \left( \frac{A}{\Phi} \right) = \frac{A}{\Phi} \left( \frac{1}{A} \frac{dA}{d\omega} - \frac{1}{\Phi} \frac{d\Phi}{d\omega} \right) \quad (14)$