非线性控制学习笔记（一），模型预测控制简单案例

去Deepseek提问弄到的简单案例，当入门理解感觉还挺合适，写在这里当个记录。

问题描述

假设我们控制一辆汽车，使其以设定的速度巡航。驾驶员设定了一个期望速度$v_{ref}$。我们的任务是设计一个MPC控制器，通过调节油门/刹车（控制输入 $u$），使汽车的实际速度$v$尽可能平稳且准确地跟踪$v_{ref}$ ，同时要满足约束：油门和刹车不能无限大，即$u_{min}\le u\le u_{max}$。

第一步：建立预测模型

首先，我们需要一个能够描述汽车速度如何响应油门/刹车的数学模型。我们使用一个非常简化的模型。
根据牛顿第二定律，假设车辆在平直路面上行驶，忽略风阻和滚动阻力，有：




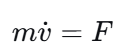
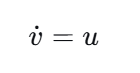
这是一个连续时间的微分方程。为了在数字控制器中实现，我们需要将其离散化。
采用前向欧拉法，采样时间为$T_s$：

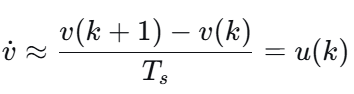
其中 k 表示第 k 个采样时刻。
整理得到我们的离散时间状态空间模型：

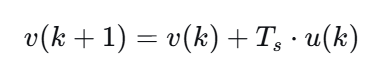
我们定义状态变量$x(k)=v(k)$。由于系统只有一个状态（速度），所以这是一个一阶系统。输出变量 $y(k)=v(k)$（我们测量速度）。
所以预测模型为：


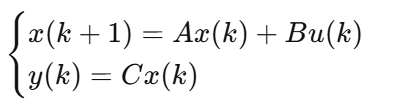
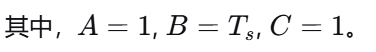
这个模型将用于预测未来时刻的系统状态。

第二步：定义优化问题

这是MPC的核心。在每个时刻 k，我们都要解决一个优化问题。

1. 预测时域

我们定义预测时域为 N。这意味着在时刻 k，我们将预测从 k 到 k + N 的未来状态。

2. 代价函数

我们希望速度跟踪准确，同时控制动作不要过于剧烈。因此，我们定义一个经典的二次型代价函数：


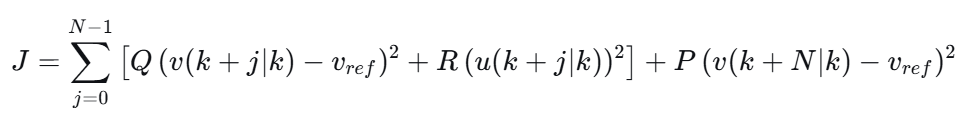
（笔者注：这里P、Q、R一般来说应该是正定矩阵，然后代价函数是二次型矩阵相乘的形式，这里因为是简单例子退化为标量）
为了简化，我们设 P=0，代价函数简化为：

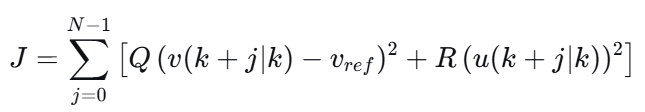
3. 约束

在我们的问题中，只有控制输入约束：

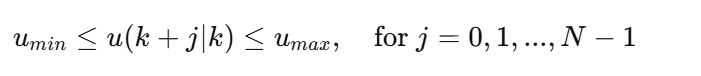
第三步：推导预测方程（核心推导）

为了求解上面的优化问题，我们需要将代价函数 $J$ 中的未来状态 $v(k+j\mid k)$用当前状态 $v(k)$ 和未来的控制输入 $u(k\mid k),u(k+1\mid k),...$ 来表示。
我们从模型 $x(k+1)=Ax(k)+Bu(k)$ 出发，进行迭代：

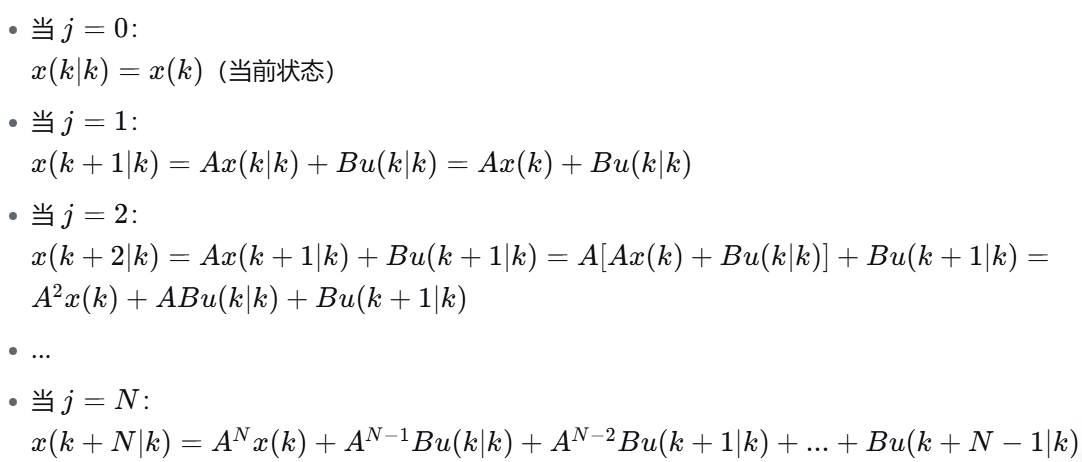
由于在我们的例子中 $A=1$, $B=T_s$，这些方程大大简化了：

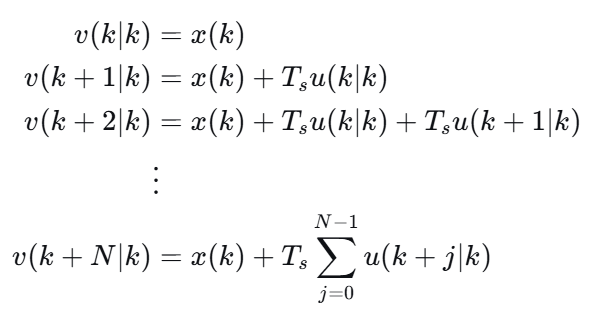
（笔者注：这里AI把表示状态的字母变量$x$和$v$混用了，应该统一一下比较好）
现在，我们可以将代价函数 J 完全表示为关于当前状态 $x(k)$ 和控制序列 ${U=[u(k\mid k),u(k+1\mid k),...,u(k+N-1\mid k)]}^T$的函数。
定义向量：

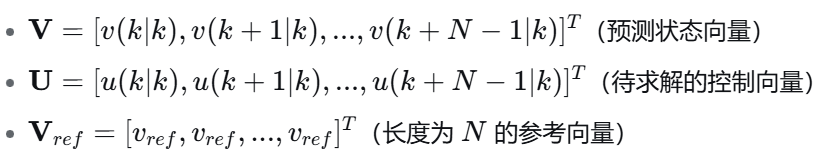
（笔者注：这里应该是简化模型把参考速度轨迹弄成定值了）
根据上面的预测方程，我们可以写出：

（笔者注：$x(k)$即当前状态$v(k)$）
其中：

现在，代价函数可以写成向量形式：

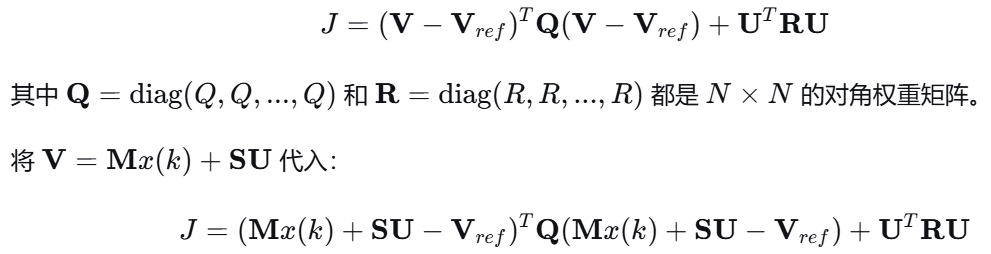
第四步：求解优化问题并应用

上面的代价函数 $J$ 是关于 $U$ 的二次函数，约束是 $U$ 的上下限（箱型约束）。

这是一个二次规划问题。在每一个控制周期 $k$：
1、测量或估计当前速度 $v(k)$。
2、求解如下QP问题：

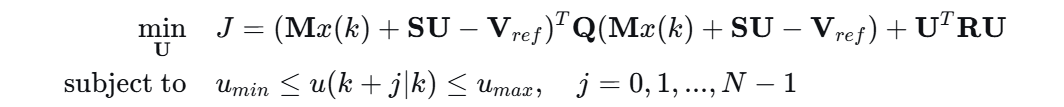
（笔者注：后面笔者有时间再去研究一下QP问题的求解，另外再发一篇笔记）
3、求解器会返回最优的控制序列${\mathbf{U}}^{\ast }=[u^{\ast }(k\mid k),u^{\ast }(k+1\mid k),...,u^{\ast }(k+N-1\mid k)]$。
4、MPC控制器只取这个序列的第一个元素 $u^{\ast }(k\mid k)$ 作为实际的控制输入$u(k)$施加给汽车。
5、到下一个采样时刻 $k+1$，重复整个过程（测量$x(k+1)$，重新求解优化问题）。

总结与直观理解