论文笔记：三维速度障碍法（Three-Dimensional Velocity Obstacle，3DVO）

前言

原论文标题：《Three-Dimensional Velocity Obstacle Method for Uncoordinated Avoidance Maneuvers of Unmanned Aerial Vehicles》，论文标题太长，没法放到这篇文章的标题上。
DOI：10.2514/1.g001715
这篇论文是笔者读研的时候曾经引用过的论文，也尝试复现过它的方法。最近求职的时候需要复盘自己以前做过的课题，所以把论文中的方法放到笔记里做个记录。
三维速度障碍法（Three-Dimensional Velocity Obstacle，3DVO）的基础是速度障碍法（Velocity Obstacle，VO），VO是一种经典的底层避障算法，具体原理这篇文章介绍得比较好：
https://zhuanlan.zhihu.com/p/662684761
3DVO除了把VO拓展到三维空间，还增加了许多细节的设计，下面章节介绍3DVO的具体实现。

论文中的一些相关的数学概念

碰撞锥

3DVO算法的背景是无人机避障，所以引入了保护区（protected zone）的概念，说白了就是以移动障碍物为中心，半径为$r_{pz}$的一个球体，双方距离小于该球体半径，视为碰撞：

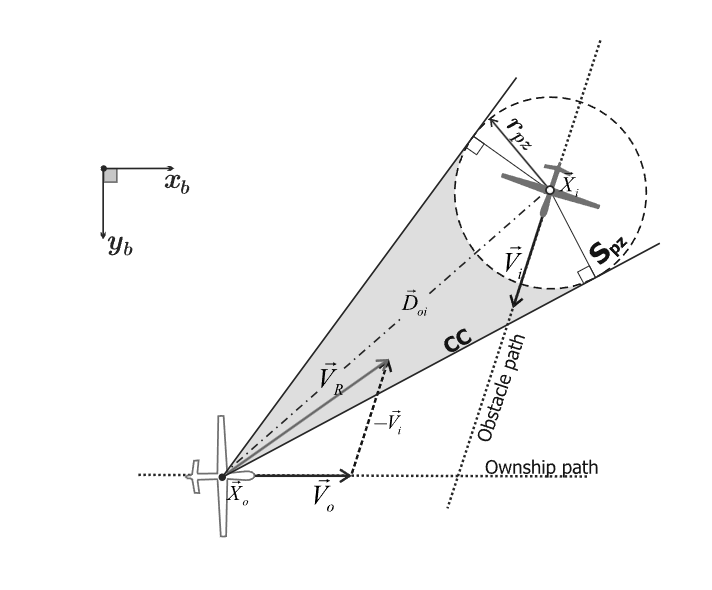
位于坐标$X_o$处的无人机为己方（owner）操控的无人机，位于坐标$X_i$处的无人机为移动障碍物，且双方无任何通信或合作关系（说白了，把移动障碍物当傻子，移动障碍物行为不可预测）。和VO算法类似，3DVO中只要$X_o$相对于$X_i$的速度$V_R$的延长线经过保护区，则有碰撞危险（前提是双方一直保持速度不变），延长线经过球形保护区的速度矢量集合组成一个锥体（见上图），称为碰撞锥（Collision Cone，CC）。

VO集

碰撞锥是相对速度$V_R$的危险集合，但我们的研究对象是己方无人机避障，需要的是己方无人机绝对速度$V_o$的危险集合。己方无人机绝对速度$V_o$的危险集合就是所谓的VO集（velocity obstacle set，VO set）。VO集的获取很简单，直接将碰撞锥的顶点沿移动障碍物的速度矢量平移即可（数学表达和经典的速度障碍法类似，可翻阅上面贴的相关文章）：

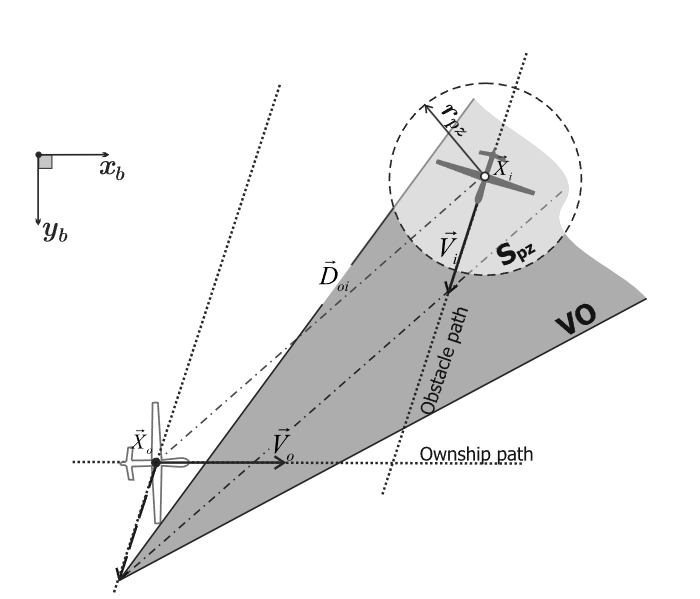
当己方无人机绝对速度$V_o$的终点在VO集里面时，意味着有碰撞危险，需要避障。
VO集只和两者的相对位置以及移动障碍物的绝对速度有关，和己方无人机的绝对速度无关。
画成三维形式：

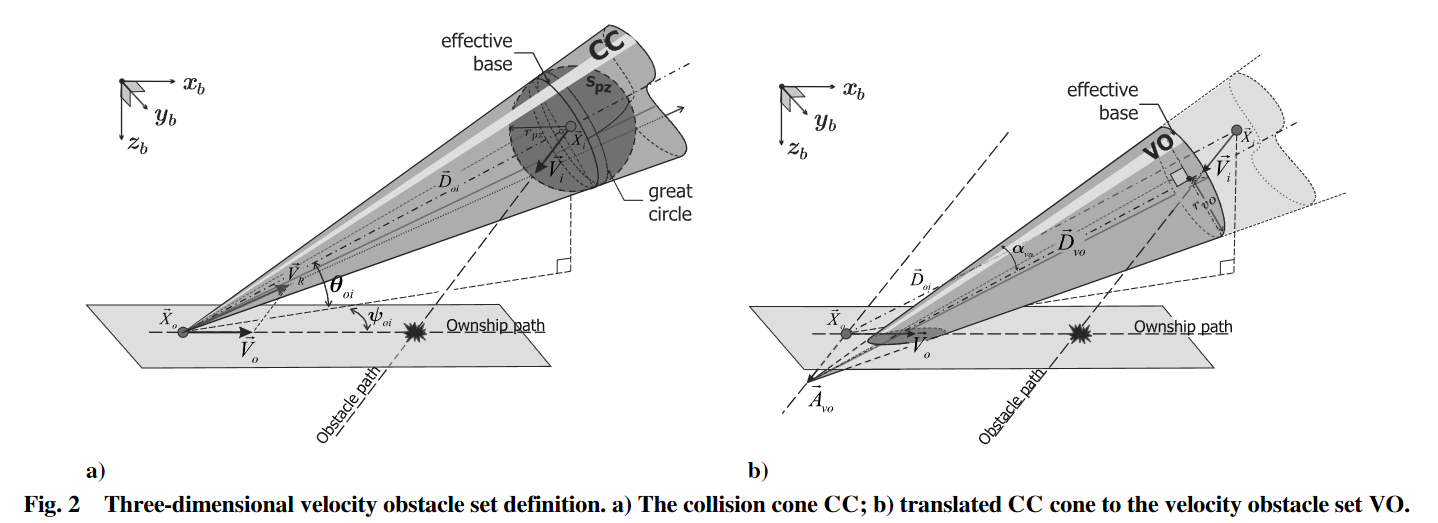
带缓冲区的速度集（The Buffer Velocity Set）

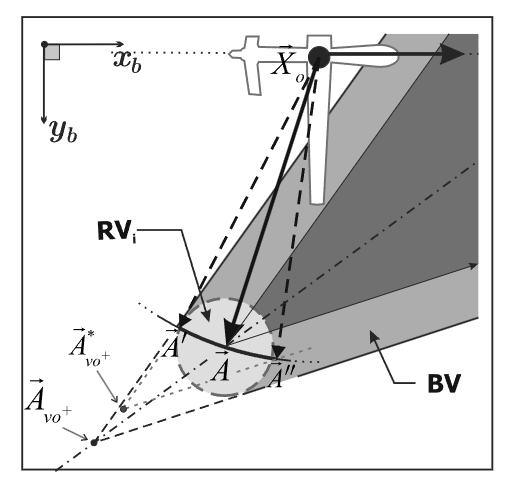
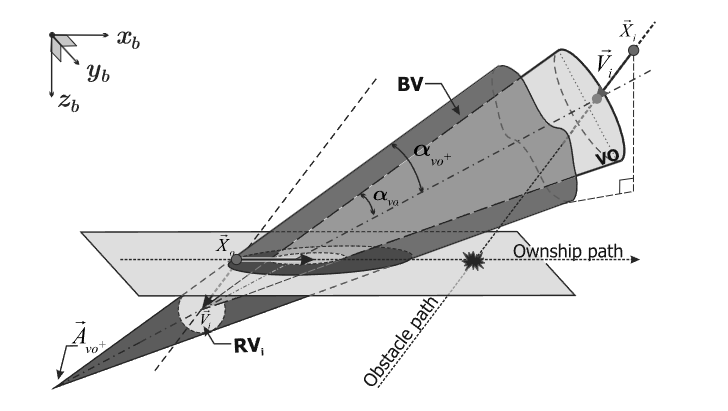
论文中考虑了移动障碍物并非匀速直线运动，而是存在一定的机动性的情况。文中假设障碍物的速度矢量$V_i$在一个时间步内会发生一定范围内的方向变化（大小不变），该范围内的所有$V_i$的终点会构成一个圆弧（见下图），称为$R{V}_i$集。

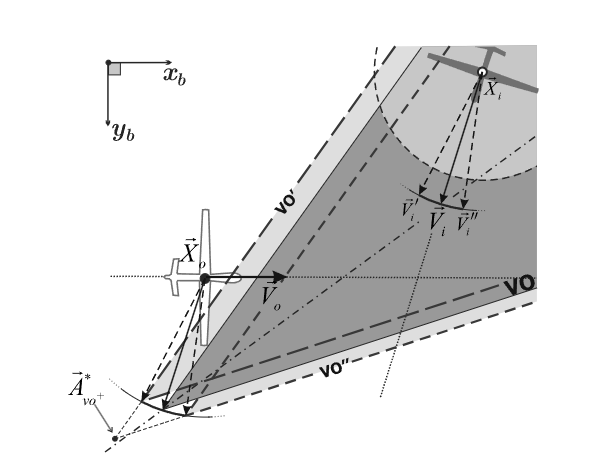
把原来的VO集沿着对称线往锥体的顶点方向平移，直到把圆弧都包进锥体中，得到一个新的集合VO+，由原来的VO集和外层包裹的缓冲区BV集组成，见下图：

避障平面

这个设计个人觉得比较有意思，目的是让己方的飞行器仅在某个二维平面完成避障，把三维的避障问题简化为二维。
既然是在二维平面完成避障，那么己方的飞行器和其绝对速度$V_o$必然在该平面上，这样的平面理论上可以画出无数个，它们全都经过己方的飞行器和其绝对速度$V_o$矢量，如下图所示：

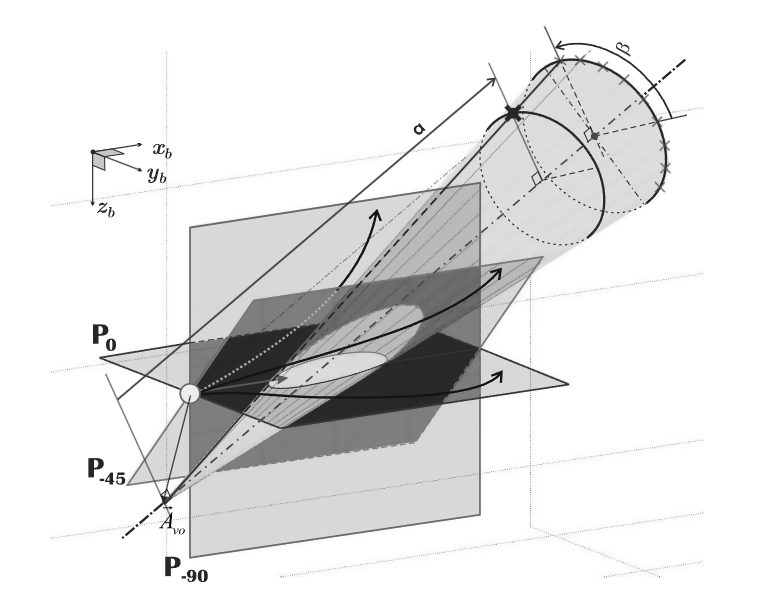
每个避障平面都可以经由某个基准平面绕$V_o$旋转angle°得到，用$P_{angle}$来区分这些平面，其中$P_0$为基准平面（笔者注：这里论文作者没有说明基准平面的设置方法，笔者复现时把与航迹坐标系的XOY平面平行，且经过$V_o$的平面设为了基准平面）。
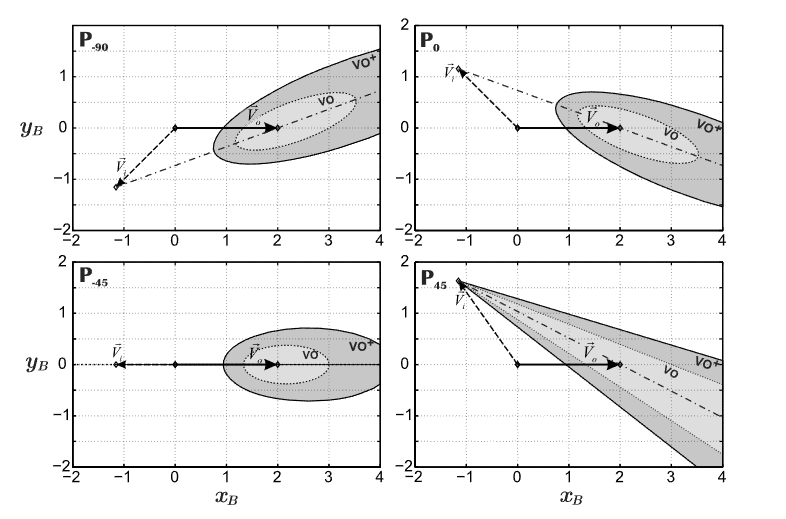
论文中根据旋转角度分了12个平面，根据高中数学，每个平面都可能和VO集相交形成圆锥曲线，或退化形式比如没有底的三角形、射线、点等。此时在二维平面上避障问题的VO集可能不再是圆锥或者三角形，而是圆锥曲线形状，如下图所示：

3DVO避障流程

三种模式

3DVO 包括三种模式：避障模式（Avoid Mode）、保持模式（Maintain Mode）、
任务模式（Mission Mode），其模式切换根据飞行器速度 𝒗 是否处于 VO 集，以及
飞行器与障碍物之间的距离来决定。

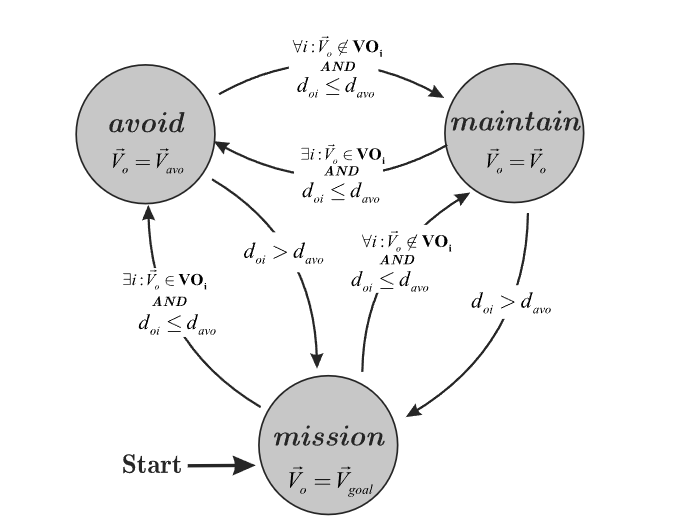
（1）如果己方无人机的速度矢量包含在 VO 集中，并且己方无人机与障碍物之间
的距离小于避障距离$d_{avo}$（可以理解为己方无人机的感知距离），则 3DVO 将处于避障模式。在避障模式中，3DVO将基于避障平面和 VO 集确定避障速度矢量，然后使己方无人机以该避障速度矢量飞行。
（2）如果己方无人机与障碍物之间的距离小于避障距离，但己方无人机的速度矢量不包含在 VO 集中，则 3DVO 将处于保持模式。在保持模式下，3DVO 将使己方无人机以当前速度矢量匀速直线飞行。
（3）如果己方无人机与障碍物之间的距离大于飞行器的感知范围，则 3DVO 将处于任务模式。在任务模式中，3DVO 将引导己方无人机维持或恢复其原来的海拔、航线和空速。

避障面选择

在避障模式中，3DVO算法会构建VO集以及12个避障平面，在这些避障平面中需要选择一个来进行避障。选择避障平面的时候会先排除掉平面上的VO集为三角形和双曲线形的，前者是因为$V_o$和$V_i$都在避障平面上，导致避障难度上升，后者没太看懂作者的意思，猜测是双曲线形碰撞锥选择的余地小，或者是虽然避免了共面但还是比较接近共面。
排除掉上面的避障平面后，接下来比较避障时的速度转向需求，选择最佳的避障平面。速度转向需求由可达速度$E_{vo}$与当前速度$V_o$的夹角来决定。可达速度可通过以当前速度$V_o$的模为半径，飞行器所在位置为圆心的圆与平面上的VO集边缘之间的交点来选择，在多个$E_{vo-x}$中选择具有最小夹角的速度矢量作为可达速度，该最小夹角便可以用于衡量所在避障面转向需求，如下图所示。

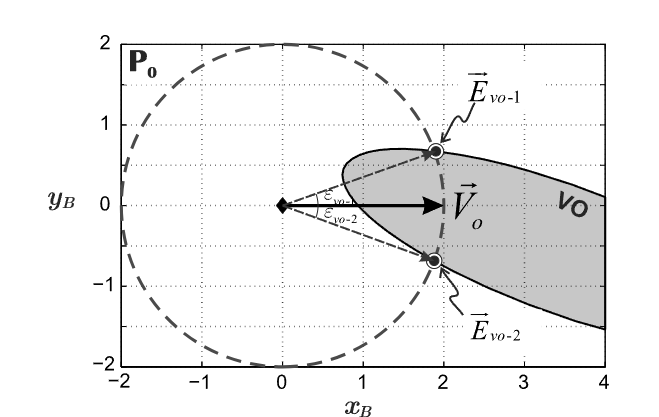
夹角最小的避障平面，即为最佳的避障平面。

避障速度的计算

选好避障面，就可以计算避障速度了。
选定好最佳的避障平面之后，无人机将根据选定的$E_{vo}$，提供一条以特定角速
率${\omega }_{avo}$进行纯转弯的避障路线，直到速度矢量$V_o$与$E_{vo}$重合。
说白了，就是让速度矢量$V_o$匀速转向，己方无人机以${\omega }_{avo}$转弯但保持速度大小不变，如下图所示。

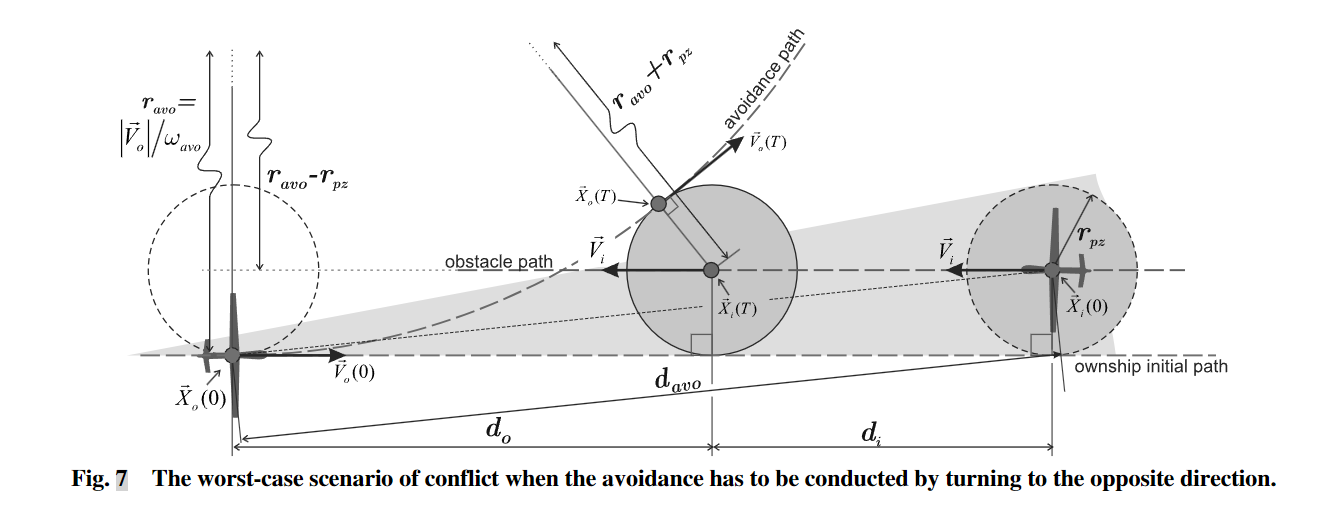
一般来说向左或向右转，能得到两个临界${\omega }_{avo}$的解（比如上图中的无人机除了虚线圆弧路径，保持${\omega }_{avo}=0$，也就是直线走，也不会撞上障碍物），但在论文中是按最坏情况去考虑，也就是选择两个临界${\omega }_{avo}$的解中较大值，然后在这个临界值的基础上再增加10%，才得到最终的${\omega }_{avo}$。然后以${\omega }_{avo}$让$V_o$往$E_{vo}$减小的方向去旋转。根据${\omega }_{avo}$和时间步长，可以很容易就得到无人机下一时刻的目标速度矢量。

笔者的一些补充

论文中其实还提了多障碍物的情况，无非就是多画几个碰撞锥，流程和单个障碍物差不多。
论文的方法看起来每一步都没有涉及太高深的理论，但笔者在尝试代码复现的时候，发现计算量还是不小，涉及很多循环遍历（获取和搜寻最优$E_{vo}$）、不同坐标系之间的坐标转换以及方程的求解，尤其是计算${\omega }_{avo}$的时候，还出现了方程没有解析解必须采用数值法求解的情况，这又进一步增加了算法的复杂度。最后代码运行的时候，发现速度并没有很快，这相当于速度障碍法原有的计算简单的优势，因为打了太多补丁后，也不复存在。不知道论文原作者的代码是怎么实现的，有没有规避这些问题。

笔者根据自己理解复现的代码：
https://github.com/ouClassmate/Three-Dimension-Velocity-Obstacle-X-Plane.git