一种2.5吉赫兹低功耗、高Q值、可靠的有源带通滤波器设计
摘要
本文提出了一种基于电压差分跨导放大器(VDTA)实现的全集成射频带通滤波器的可变性感知且可靠的设计。该滤波器具有高频工作、低功耗、高品质因数等特点,并对工艺、电压和温度(PVT)变化不敏感。已进行灵敏度分析以评估寄生元件存在下的电路性能。这种无电感方法适用于射频前端的集成构建模块,从而消除了收发器中对片外滤波器的需求。该滤波器中心频率为2.511吉赫,3‐dB带宽为36.21兆赫,从 ±1 V电源消耗 0.168mA电流,实现72.6dB的电压增益、69.34的品质因数以及~29.6dB的噪声系数。此外,其动态范围为125.84dB‐Hz, 1分贝压缩点为 −1.5dBm,对应的品质因数高达94dB。
索引术语
有源电感;带通滤波器;可靠性;跨导; VDTA;CMOS射频集成电路。
I. 引言
当前无线电收发器中的大多数商用滤波解决方案采用 片外无源元件实现,例如LC、陶瓷和电声元件。这些片外 滤波器体积庞大、成本高,且无法电子调谐,从而降低了 设计灵活性。如今,半导体和射频(RF)技术市场快速发 展,导致在单芯片上集成了支持不同数据速率和频段的多 种通信标准的无线系统。片上射频带通滤波器是全集成射 频收发器设计中的关键功能模块[1]。由于对小分数带宽、 高品质因数、高压缩点、低噪声系数、低功耗、高动态范 围以及对工艺、电压和温度(PVT)变化的免疫性等严格 要求,片上带通滤波器的性能受到限制。[2],[3]因此,设 计全集成高性能射频带通滤波器仍然是一个主要挑战。
文献中存在多种集成射频带通滤波器拓扑,如开关电容滤波器、 有源RC滤波器、MOSFET‐C滤波器、Q增强型LC滤波器和G m ‐C滤 波器。
每种滤波器拓扑都存在一种或多种限制,从而限制了 其在高频集成应用中的使用。开关电容滤波器存在时钟馈 通问题[4],[5], ,而基于有源RC积分器[6]和 MOSFET‐C滤波器[7]的连续时间滤波器由于反馈中所使 用的运算放大器的有限增益带宽积,导致高频工作能力受 限。在所有滤波器拓扑中,Q增强型LC滤波器和Gm‐C滤 波器最适合在千兆赫频率以上实现。Q增强型LC滤波器采 用有损LC谐振槽,并通过负阻网络[8]‐[10]补偿与单片电 感器相关的损耗,从而提高有效品质因数。然而,由于以 下原因,在射频频率下集成LC滤波器非常困难:(a)使用 体积庞大的电感器,这些电感器不符合工艺缩放规律; (b)单片电感器的品质因数(通常为10或更低)[11],适中 偏低;(c)片上螺旋电感器相关的损耗(如由串联电阻Rs 表示的金属欧姆损耗、衬底中的涡流损耗以及由衬底电阻 Rsub引起的电阻损耗) ;以及(d)调谐能力有限和动态范 围较低。LC滤波器的品质因数直接取决于谐振槽电感器 的品质因数。已有多种尝试通过改变制造步骤来提升在标 准射频CMOS工艺流程中单片电感器的品质因数(Q< 20)。
然而,复杂且额外的制造步骤不仅提高了制造成本,还降 低了大规模生产的可靠性[12]‐[14]。通过使用有源器件模 拟其行为,可以消除在标准硅工艺中使用单片电感器所产 生的此类问题。
使用两个跨导器和一个积分电容构成反馈环路(回转 器‐C)可以模拟电感[15],[16]。在CMOS设计流程中,单 个晶体管的过渡频率(f T )可高达数百千兆赫,使得器件 能够在千兆赫频率范围内工作。高频Gm‐C滤波器设计中的 一个基本问题是在单位增益频率[17]‐[20]处积分器的相移 误差。该相移问题由积分器的有限直流增益以及高频寄生 极点和零点引起。其他问题包括其对工艺、电源电压和温 度变化的敏感性[1], 、小动态范围以及非常低的品质因数 (FOM)[21],[22]。
本文解决了上述问题,提出了一种基于有源电感的射 频带通滤波器,该滤波器实现了高品質因數、高动态范围、 高优值、可调谐振频率、低功耗,并且对工艺、电压、温 度变化不敏感。提出的设计为无电阻、无电感,仅采用有 源元件(晶体管)和全部接地无源元件(电容器)[23], , 从而验证了其工艺可扩展性以及适用于高频全集成应用。
本文的结构如下。第二节讨论了先进的电压差分跨导 放大器(VDTA)及其有源电感设计,并介绍了提出的 VDTA架构。第三节阐述了射频带通滤波器的设计方法, 并分析了VDTA寄生参数和电流镜失配对滤波器性能的影 响。此外,讨论了Gm‐C滤波器中的相移误差问题,并将其 动态范围与其他滤波器拓扑进行了比较。第四节提供了仿 真结果,并将所提出滤波器的性能与现有的带通滤波器拓 扑进行了对比。第五节给出了版图后仿真结果,并验证了 设计的可扩展性。第六节研究了工艺、电压、温度变化对 所提出滤波器设计指标的影响。最后,第七节给出了结论。
II. VDTA(电压差分跨导放大器)
文献中提供了多种由不同高性能有源基本单元构成的 电路拓扑,用于实现有源电感[24]‐[29]。电压差分跨导放 大器(VDTA)是一种先进的有源基本单元,广泛应用于 滤波器、振荡器、电感模拟器等各种模拟信号处理场合 [30]−[32]。VDTA是一种具有电子可调谐跨导的多输出跨 导放大器,这使其成为电子可控有源网络综合的理想选择。 此外,VDTA还具有所有节点高阻抗的额外优势,从而允许级 联使用。
A. 电路描述
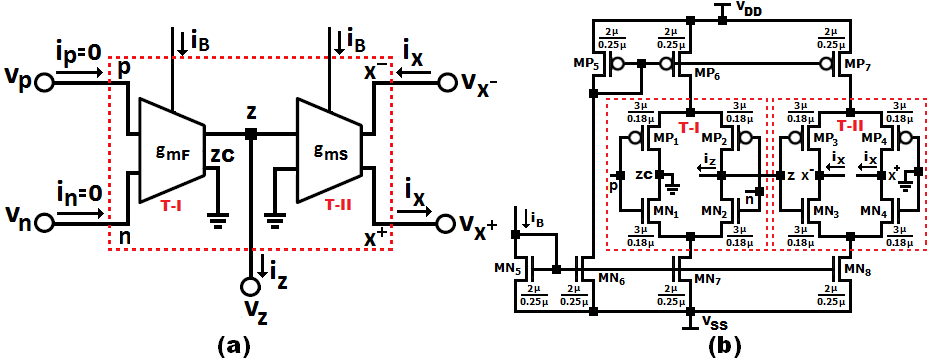
电压差分跨导放大器(VDTA)是一种通用的六端子 (p、n、z、zc、x− 和x+)有源基本单元,可用于多种模 拟信号处理应用。它在电压模式和电流模式下均具有灵活 的操作特性[24]。可以将其视为由两个级联的跨导(T‐I 和T‐II)组成的网络,如图1(a)所示[33]。VDTA包含一 对高阻抗输入端子“p”和“n”;辅助端子“z”和“zc”; 以及一对高阻抗输出端子“x+”和“x−”。流入高阻抗输 入端子的输入电流(ip、in)为零。输入电压之差(vp −-vn) 通过第一个跨导(T‐I)被转换为输出电流(iz)。然后, 在第二个跨导(T‐II)的帮助下,辅助端子z上的电压降 (vz)被转换为端子x+ 和x−处的输出电流。当需要多个 电流iz 的副本以提高VDTA的通用性时,使用端子“zc”。 流经端子x+ 和x− 的电流大小相等、方向相反,用ix表示。
理想VDTA的端口关系可用以下矩阵方程组描述
$$
\begin{bmatrix}
i_p \
i_n \
i_z \
i_{zc} \
i_x
\end{bmatrix}
=
\begin{bmatrix}
0 & 0 & 0 & 0 & 0 \
0 & 0 & 0 & 0 & 0 \
0 & 0 & g_{mF} & -g_{mF} & 0 \
0 & 0 & 0 & 0 & 0 \
0 & 0 & \pm g_{mS} & 0 & 0
\end{bmatrix}
\begin{bmatrix}
v_p \
v_n \
v_z \
v_{zc} \
v_x
\end{bmatrix}
$$
(1)
其中,gmF 和gmS 分别是VDTA第一级和第二级的跨导。
传统VDTA的CMOS实现如图1(b)[34]所示。跨导T‐I和 T‐II采用Arbel‐Goldminz跨导实现[35]。
这些跨导可以通过外部直流偏置电流i B 进行电子调节,并 可近似为
$$
g_{mF} \approx \left( \frac{g_{m1} + g_{m2}}{g_{m3} + g_{m4}} \right) \cdot \left( \frac{g_{m1} + g_{m2}}{g_{m3} + g_{m4}} \right)
$$
(2)
$$
g_{mS} \approx \left( \frac{g_{m5} + g_{m6}}{g_{m7} + g_{m8}} \right) \cdot \left( \frac{g_{m5} + g_{m6}}{g_{m7} + g_{m8}} \right)
$$
(3)
其中,gmi 是定义的第ith 个MOS晶体管的跨导值
$$
g_{mi} \approx i_{Bi} \cdot C_{ox} \cdot \mu_j \cdot \left( \frac{W}{L} \right)_i
$$
(4)
其中,i= 1、2…iBi为ith晶体管的偏置电流;Cox为单位面 积栅氧化层电容; $\mu_j$为晶体管的有效载流子迁移率(j=为 PMOS或NMOS);(W/L)分别为ith晶体管的宽长比。
B. 使用VDTA的有源电感设计
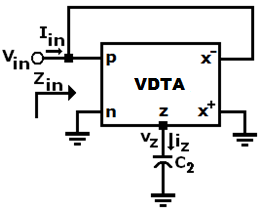
图2展示了使用VDTA合成接地有源电感的设计方法。 该结构包含一个单一的VDTA元件和一个电容C2。端子p和 x−连接在一起,端子n和x+接地。
使用(1)分析该电路可得到输入阻抗的下列表达式
$$
Z(s) = \frac{V_{in}(s)}{I_{in}(s)} = \frac{sC_2}{g_{mF} \cdot g_{mS}}
$$
(5)
因此,该电路实现了一个具有等效电感的接地电感器
$$
L_{eq} = \frac{C_2}{g_{mF} \cdot g_{mS}}
$$
(6)
该Leq值可以通过VDTA的跨导gmF或gmS.中的任意一个进 行电子调节。
C. VDTA寄生参数对电感的影响
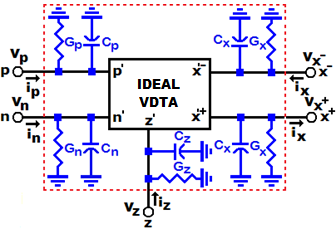
每个VDTA(输入/输出)端子都具有相关的寄生电容 和电导,这些会影响系统性能。考虑到VDTA的寄生端子 阻抗,例如p端有限的寄生电导Gp与电容Cp并联,n端有限 的寄生电导Gn与电容Cn并联,z端有限的寄生电导Gz与电 容Cz并联,以及x−端有限的寄生电导Gx与电容Cx并联, VDTA的非理想电路表示如图3所示。
在理想情况下,推导(5)时忽略了寄生电导Gp、Gn、 Gz、Gx以及杂散/寄生电容Cp、Cn、Cz、Cx 。然而,如果 考虑这些寄生元件,则有源接地电感的非理想等效输入阻 抗可计算为
$$
Z’(s) = \frac{sC_2(G_z + sC_z)}{G_e’ + s(C_e’ + C_z) + s^2 C_2(G_e’G_z + G_z^2)}
$$
(7)
其中,
$$
C_z’ = C_2 + C_z
$$
(8)
$$
C_e’ = C_x + C_p
$$
(9)
$$
G_e’ = G_x + G_p
$$
(10)
因此,电容C2必须选择为满足以下条件,即C2>> Cz且 sC2>> Gz。由于在有源电感综合过程中,端子n和x+ 相关 的寄生电容和电导被短接到地,因此在分析中不予考虑。
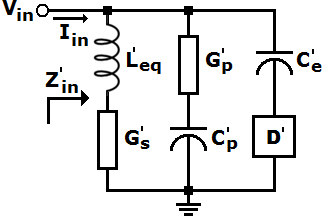
由式(7)推导出的有源电感的非理想等效电路如图4所示。 L’ e q、G’ p、G’ s 和C’ p 的值可以近似为
$$
L’_{eq} = \frac{C_2}{G_e’ + G_z}
$$
(11)
$$
G_s’ = \frac{G_e’ \cdot G_z}{G_e’ + G_z}
$$
(12)
$$
C_p’ = \frac{G_e’ \cdot C_z}{G_e’ + G_z}
$$
(13)
$$
C_p’ = \frac{C_e’ \cdot G_z}{G_e’ + G_z}
$$
(14)
$$
C_p’ = \frac{C_e’}{D}
$$
(15)
D. 灵敏度性能与比较
电感L’ e q 相对于各个构成无源和有源元件的灵敏度 (定义为电路元件参数发生微小变化时响应变化的程度) 等于
$$
S_{L’ {eq}/C_2} = S {L’ {eq}/C_z} = S {L’ {eq}/C_x} = S {L’_{eq}/C_p} = 0
$$
(16)
$$
S_{L’ {eq}/G_z} = S {L’_{eq}/G_e’} = -\frac{G_z}{G_e’ + G_z}
$$
(17)
$$
S_{L’ {eq}/g {mF}} = S_{L’ {eq}/g {mS}} = -\frac{g_{mF} \cdot g_{mS}}{G_e’ + G_z}
$$
(18)
可以观察到,电感值对无源和有源元件的灵敏度较低,且小于1。
为了最小化寄生电导的影响并降低与其相关的损耗,在 传统VDTA中集成了两对交叉耦合的NMOS晶体管,如图5 所示。晶体管对M16和M17实现了负阻拓扑,从而最小化z 和zc端子处的寄生电导。类似地,晶体管对M18和M19最小 化x−和x+[36]端子处的寄生电导,从而显著提高了增益和 品质因数。因此,z和x−端子处的补偿后的寄生电导为
$$
G_{zR} = G_z - G_{nR}
$$
(19)
$$
G_{eR}’ = G_e’ - G_{nR}
$$
(20)
其中,GnR为负电导。
因此,基于所提VDTA的有源电感的等效电感L’’ e q 可近似为
$$
L’‘ {eq} = \frac{C_2}{G {eR}’ + G_{zR}}
$$
(21)
L’’ e q对寄生电导的灵敏度可计算为
$$
S_{L’‘ {eq}/G {zR}} = S_{L’‘ {eq}/G {eR}’} = \frac{1}{1 + k_1}
$$
(22)
这低于传统VDTA(见图1(b))的灵敏度,因为k 1 <1。
类似地,L’’ e q 对跨导gmF 、gmS 的灵敏度被评估为
$$
S_{L’‘ {eq}/g {mF}} = S_{L’‘ {eq}/g {mS}} = \frac{1}{1 + k_2}
$$
(23)
这高于传统VDTA(见图1(b))的灵敏度,因为k2>1。因此, 基于所提VDTA的有源电感表现出更优的灵敏度性能,因 为它减小了寄生电导Gz、Gx对电感值的影响。此外,其电 感对跨导gmF、gmS更加敏感,这是有利的。
III. 射频带通滤波器设计
在本节中,介绍了使用基于所提VDTA的接地电感实 现射频有源带通滤波器(BPF)的设计。采用交叉耦合负 阻方法[36]来补偿寄生损耗,从而提高了增益和品质因数。 还研究了电流源失配对滤波器设计指标的影响。此外,讨 论了相位误差问题,并将Gm‐C滤波器的动态范围与其它现 有拓扑结构进行了比较。
A. 有源BPF设计方法
所提出的有源带通滤波器设计(见图6)主要由一个二 极管连接型有源电导gde q、一个电容(C1)和一个模拟接地 有源电感(Le q)组成。
滤波器的传递函数可以被建模为
$$
\frac{V_o(s)}{V_{in}(s)} = \frac{Ks/C_1}{s^2 + \frac{g_{deq}}{C_1}s + \frac{1}{C_1C_2g_{mF}g_{mS}}}
$$
(24)
其中,K是滤波器增益,Le q 是由(6)给出的等效电感,g de q 是表示为二极管连接型电导的
$$
g_{deq} = \frac{g_{d20} \cdot g_{d21}}{g_{d20} + g_{d21}}
$$
(25)
其中,gd20 和gd21 分别是二极管连接的PMOS和NMOS晶体管的 电导。
滤波器参数即谐振频率(ω0) 、3‐dB带宽(BW)和品质因 数(Q)可从(24)中推导得出
$$
\omega_0 = \sqrt{\frac{g_{mF} \cdot g_{mS}}{C_1C_2}}
$$
(26)
$$
BW = \frac{g_{deq}}{C_1}
$$
(27)
$$
Q = \frac{1}{2} \cdot \sqrt{\frac{C_1}{C_2}} \cdot \frac{\sqrt{g_{mF} \cdot g_{mS}}}{g_{deq}}
$$
(28)
B. 高Q值带通滤波器设计
积分器是Gm‐C滤波器的基本组成部分,通过使用跨导 器加载积分电容[17]‐[20]来实现。滤波器设计指标,如动态 范围、功耗等,不仅依赖于滤波器本身的特性(即截止频 率、品质因数、带宽),还依赖于积分器特性,如直流增 益、单位增益频率、寄生极点和零点、噪声以及线性度。 因此,改善上述积分器特性可转化为最佳滤波器性能。理 想积分器在所有频率下均表现出–π/2的相位。然而,高频 Gm‐C滤波器对积分器中的非理想性极为敏感。正是由于这 些非理想性,积分器的相位响应偏离了−π/2的理想响应, 这种偏差称为附加相移误差。实际积分器的相位响应由以 下给出
$$
\phi(\omega) \approx \frac{\pi}{2} + \frac{\omega}{\omega_t} + \frac{\omega}{\omega_z} - \frac{\omega}{\omega_p}
$$
(29)
这里,gm0 是直流跨导,R 0 是有限输出阻抗, ω t 是单位 增益频率, ω p 和ω z 分别表示高频寄生极点和零点。因此, 由于有限直流增益以及高频寄生极点和零点引起的附加相 位偏移可以被评估为
$$
\Delta \phi(\omega) \approx \frac{\omega}{\omega_t} \left( \frac{1}{g_{m0}R_0} + \frac{1}{\omega_z} - \frac{1}{\omega_p} \right)
$$
(30)
文献中报道,如果直流增益约为48dB,并且寄生极 点/零点比单位增益频率[19],[20]大250倍,则上述非理想 性的影响可以忽略不计。在实践中,可以通过使用共源共 栅输出级和/或采用负阻拓扑[18],[19]来实现或至少最小 化这些影响。然而,使用共源共栅级会因增加内部节点而 引入额外相移,从而导致可靠性降低。一种被广泛接受的 替代方案是在电路中引入负阻网络。负阻网络可补偿积分 器内的寄生损耗并提高直流增益,从而最小化输出相位的 偏移。这种最小化直接转化为滤波器品质因数的提升,因 为积分器的品质因数(Qint)与额外相移成反比。
类似的方法应用于提出的设计中,传统VDTA采用负 阻拓扑加载,且不产生任何额外的内部节点。
C. VDTA寄生参数对有源带通滤波器性能的影响
VDTA的寄生电容和电导会影响积分器特性,从而影 响滤波器设计指标,尤其是 ω 0 和Q,如前一节所述。这种 影响在千兆赫频率范围内更加严重,限制了Gm‐C拓扑的谐 振频率和品质因数,使滤波器设计极具挑战性。在VDTA 内部引入的负阻拓扑可最小化这些额外的相位损耗,从而 提升滤波器性能。
所提出的滤波器的非理想传递函数可以被评估为
$$
\frac{V_o(s)}{V_{in}(s)} = \frac{sC_2(G_{zR} + sC_z’)}{s^2R_{eq}C_2’ + s(R_{eq}g_{mF}g_{mS} + G_{zR}R_{eq} + G_{eR}’R_{eq}) + \lambda}
$$
(31)
其中,
$$
\lambda = R_{eq}C_2’G_{zR} + R_{eq}C_2’G_{eR}’ + R_{eq}C_2’G_{zR}
$$
(32)
C’ 2和R的值可以从(8)和(25)代入
$$
R = \frac{1}{g_{deq}} = \frac{g_{d20} + g_{d21}}{g_{d20} \cdot g_{d21}}
$$
(33)
该非理想传递函数可与理想情况相比较,并可计算出ω0和 Q的修正表达式。
$$
\omega_0’ = \sqrt{\frac{g_{mF} \cdot g_{mS} + g_{deq} + G_{zR} + G_{eR}’}{C_1C_2’}}
$$
(34)
and
$$
Q’ = \frac{\sqrt{g_{mF} \cdot g_{mS} + g_{deq} + G_{zR} + G_{eR}’}}{G_{zR}C_1 + G_{eR}’C_1 + g_{deq}C_2’}
$$
(35)
此外,可以确定0对其组成的寄生电容和电导的灵敏度 ω
$$
S_{\omega_0/G_{zR}} = \frac{1}{2} \cdot \frac{G_{zR} + G_{eR}’}{g_{mF} \cdot g_{mS} + g_{deq} + G_{zR} + G_{eR}’}
$$
(36)
$$
S_{\omega_0/G_{eR}’} = \frac{1}{2} \cdot \frac{G_{eR}’}{g_{mF} \cdot g_{mS} + g_{deq} + G_{zR} + G_{eR}’}
$$
(37)
$$
S_{\omega_0/C_z} = -\frac{1}{2} \cdot \frac{C_z}{C_z + C_2}
$$
(38)
$$
S_{\omega_0/C_x} = -\frac{1}{2} \cdot \frac{C_x}{C_x + C_p}, \quad S_{\omega_0/C_p} = -\frac{1}{2} \cdot \frac{C_p}{C_x + C_p}
$$
(39)
D. 跨导误差分析
由于上下电流镜的失配,导致在z或zc端口与x−或x+ 端口处复制的电流量不同,从而产生跨导误差,引起跨导 值的差异。为了描述这一效应,VDTA的端口关系可以重 写为
$$
\begin{bmatrix}
i_p \
i_n \
i_z \
i_{zc} \
i_x
\end{bmatrix}
=
\begin{bmatrix}
0 & 0 & 0 & 0 & 0 \
0 & 0 & 0 & 0 & 0 \
0 & 0 & \beta_F g_{mF} & -\beta_F g_{mF} & 0 \
0 & 0 & 0 & 0 & 0 \
0 & 0 & \pm \beta_S g_{mS} & 0 & 0
\end{bmatrix}
\begin{bmatrix}
v_p \
v_n \
v_z \
v_{zc} \
v_x
\end{bmatrix}
$$
(40)
其中,β F 和 S 分别为VDTA第一级和第二级的跨导误差参数。 β
滤波器设计指标(ω 0 和Q)在考虑跨导误差 β F 和β S 的情况下,按(41)和(42)式修改如下,即
$$
\omega_0 = \sqrt{\frac{\beta_F \beta_S g_{mF} \cdot g_{mS}}{C_1C_2}}
$$
(41)
$$
Q = \frac{1}{2} \cdot \sqrt{\frac{C_1}{C_2}} \cdot \frac{\sqrt{\beta_F \beta_S g_{mF} \cdot g_{mS}}}{g_{deq}}
$$
(42)
因此,从(41)和(42)可以看出,由于跨导误差,滤波器参数 偏离了其标称值。通过在输出级使用更高的电阻或通过电 子方式调节VDTA的跨导参数gmF或gmS.,可以将这种偏差 最小化。非理想滤波器参数相对于gmF、gmS、gd20、gd21、 C1, C2, βF和 βS的灵敏度可以计算为
$$
S_{\omega_0/g_{mF}} = S_{\omega_0/g_{mS}} = S_{\omega_0/\beta_F} = S_{\omega_0/\beta_S} = \frac{1}{2}
$$
(43)
$$
S_{\omega_0/g_{d20}} = S_{\omega_0/g_{d21}} = 0
$$
(44)
$$
S_{\omega_0/C_1} = \frac{1}{2}, \quad S_{\omega_0/C_2} = -\frac{1}{2}
$$
(45)
$$
S_{Q/g_{mF}} = S_{Q/g_{mS}} = S_{Q/\beta_F} = S_{Q/\beta_S} = \frac{1}{2}
$$
(46)
$$
S_{Q/g_{d20}} = \frac{-g_{d20}}{g_{d20} + g_{d21}}, \quad S_{Q/g_{d21}} = \frac{-g_{d21}}{g_{d20} + g_{d21}}
$$
(47)
$$
S_{Q/C_1} = \frac{1}{2}, \quad S_{Q/C_2} = -\frac{1}{2}
$$
(48)
因此,可以看出ω0和Q相对于上述参数的灵敏度较低,且小于 1。
E. 整体非理想分析
最后,综合考虑跨导误差和VDTA寄生参数这两种非 理想效应后,谐振频率(ω0)和品质因数(Q)的整体表 达式可以表示为
$$
\omega_0’ = \sqrt{\frac{\beta_F \beta_S g_{mF} \cdot g_{mS} + g_{deq} + G_{zR} + G_{eR}’}{C_1C_2’}}
$$
(49)
$$
Q’ = \frac{\sqrt{\beta_F \beta_S g_{mF} \cdot g_{mS} + g_{deq} + G_{zR} + G_{eR}’}}{G_{zR}C_1 + G_{eR}’C_1 + g_{deq}C_2’}
$$
(50)
显然,从(49)、(50)式可以看出,当寄生电导Gz和G’ e 被GnR完全抵消时,谐振频率(ω0)和品质因数(Q)的表达式将 退化为其理想的理论值。
F. 动态范围比较
动态范围是射频设计中最关键的方面之一。无论是有 源还是无源滤波器,都具有一定的动态范围。在集成接收 机设计中,有源滤波器的动态范围主要决定了接收机的动 态范围。因此,有源滤波器必须具备较大的动态范围。
用于比较不同电路的动态范围(DR)的一个简单定义如 下所示
$$
DR = \frac{P_{1dB}}{P_n}
$$
(51)
其中,P 1dB 是1‐dB压缩点,P n 是相对于1赫兹带宽的输入参考噪 声功率[3],[37]。
二阶Gm‐C带通滤波器的动态范围可以表示为
$$
DR = \frac{P_{dc}}{KTFBQ^2}
$$
(52)
其中, η为效率因子;Pdc为直流功耗;KT为玻尔兹曼常 数与开尔文温度的乘积KT;F为过剩噪声系数(始终为≥ 1), 其值取决于工艺参数和偏置条件;B为滤波器噪声带宽B, Q为滤波器的品质因数。由式(52)可知,Gm‐C滤波器的动 态范围DR与其品质因数Q的平方成反比,从而在动态范围 DR和滤波器的频率选择性之间形成折衷[22]。Gm‐C滤波器 中动态范围DR较低的原因在于:跨导器在大偏置电流下产 生的过剩噪声,以及为给电容器充电所需的动态功率。
对于Q增强型LC拓扑,动态范围DR计算为
$$
DR = \frac{P_{dc}}{(Q^2 + 1)KT F BQ}
$$
(53)
其性能优于Gm‐C结构,优势因子为Q0 2(其中Q0为片上螺 旋电感的品质因数)。然而,Q增强型LC滤波器存在电感 损耗和低品质因数的问题。此外,它们需要较大的芯片面 积,限制了其在集成低功耗应用中的使用。文献[38]中已报 道了一种基于开关Gm‐C的N路径带通滤波器结构。在N路 径滤波器中,动态范围DR与滤波器的品质因数(Q)无关, 因此在Q增强型LC和Gm‐C拓扑结构中实现了最佳的DR性 能。但需要注意的是,这种性能提升是以增加电路复杂度 为代价的。N路径滤波器采用电阻反馈放大器,需要额外 的本振生成电路,并且还存在开关非零导通电阻的问题。
本文设计了一种简单的Gm‐C滤波器,在不增加复杂性和芯 片面积的情况下,实现了与其他所有集成滤波器相当的动 态范围性能。
IV. 仿真结果与讨论
使用由亚利桑那州立大学(ASU)的纳米级集成与建 模(NIMO)小组基于BSIM4CMOS技术模型[39],[40] 开发的45纳米预测技术模型(PTM),对提出的设计以及 用于比较的设计进行了仿真。采用Cadence的Virtuoso ADE对滤波器性能进行评估。
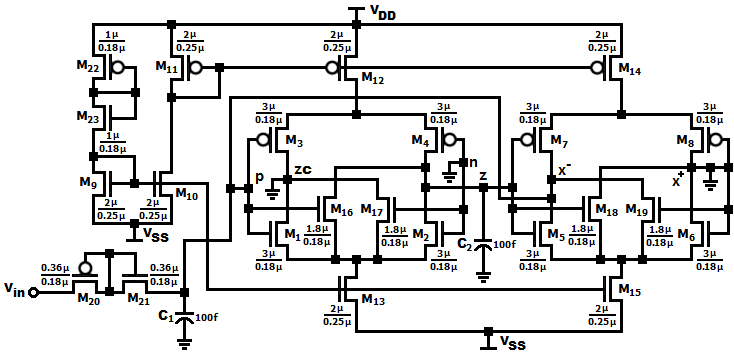
图5所示的提出VDTA、图6所示的带通滤波器以及图 1所示的传统VDTA在仿真中所用的所有器件(M1至 M23)的尺寸(沟道宽度W以及沟道长度L)如表I所示。
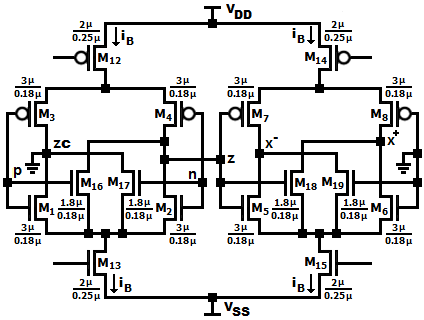
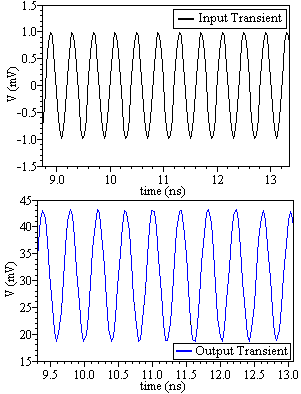
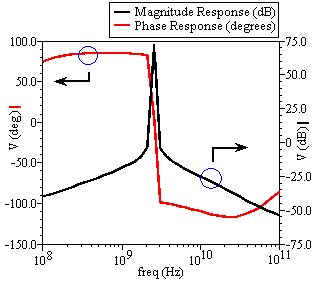
图6所示的提出带通滤波器在 ±1 V电源电压下进行仿真, 电容器C 1 和C 2 的值为100飞法。滤波器的瞬态响应以及增 益和相位响应分别如图7和图8所示。该滤波器在 2.511GHz谐振频率处实现了72.76分贝的增益。
| 器件 | 器件 Type |
| 器件 | 器件 Type | 沟道宽度(W) | 沟道长度(L) | 使用于 |
| — | — | — | — | — |
| MN1/2/3/4 | NMOS | 3 μm | 0.18 μm | 图1 |
| MP1/2/3/4 | PMOS | 3 μm | 0.18 μm | 图1 |
| MN5/6/7/8 | NMOS | 2 μm | 0.25 μm | 图1 |
| MP5/6/7 | PMOS | 2 μm | 0.25 μm | 图1 |
| M1/2/5/6 | NMOS | 3 μm | 0.18 μm | 图5,6 |
| M3/4/7/8 | PMOS | 3 μm | 0.18 μm | 图5,6 |
| MN1/2/3/4 | NMOS | 3 μm | 0.18 μm | 图1 |
| M9/10 | NMOS | 2 μm | 0.25 μm | 图6 |
| M11/12/14 | PMOS | 2 μm | 0.25 μm | 图5,6 |
| M13/M15 | NMOS | 2 μm | 0.25 μm | 图5,6 |
| M16/17/18/19 | NMOS | 1.8 μm | 0.18 μm | 图5,6 |
| M20 | PMOS | 0.36 μm | 0.18 μm | 图6 |
| M21 | NMOS | 0.36 μm | 0.18 μm | 图6 |
| M22 | PMOS | 1 μm | 0.18 μm | 图6 |
| M23 | NMOS | 1 μm | 0.18 μm | 图6 |
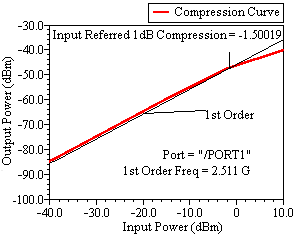
所得的3‐dB带宽等于36.21兆赫。由于滤波器增益较高,达 到了69.34的品质因数。此外,该滤波器消耗0.168毫瓦, 表现出−1.5dBm的1‐dB压缩点(如图9所示)和29.62分 贝的噪声系数。
表II报告了所提出滤波器的噪声性能及其动态范围。 表II中提到的噪声参数是在不同的频率跨度上估算的,因 为噪声是基于带宽计算的。为了分析而特别选择的三个带 宽分别为1赫兹、1兆赫和滤波器噪声带宽(56.84兆赫)。 这样做是为了确保能够公平地比较文献[41]中报道的不同滤 波器拓扑。
二阶带通滤波器的噪声带宽(B0)由[42]给出
$$
B_0 = \frac{\pi f_0}{2Q_0} = \frac{\pi \cdot 2.511 \times 10^9}{2 \cdot 69.34}
$$
(54)
其中,f0为谐振频率,Q0为品质因数,BW为滤波器的 3‐dB带宽。根据(54),所提带通滤波器的噪声带宽评估为 56.84兆赫。
归一化到1赫兹带宽的噪声功率称为点噪声。通过将滤 波器噪声电压除以滤波器噪声带宽B的平方根,可得到点噪 声。由于大多数频域应用涉及功率(分贝毫),跨50欧姆的 输入/输出点噪声电压v(伏)可转换为功率Pn(dBm),如[43] 所示。
$$
P_n(dBm) = 10 \log_{10} \left( \frac{v^2}{50} \times 1000 \right)
$$
(55)
在2.511吉赫时,所提出滤波器的输入参考点噪声被确定为 9.601×10⁻⁸ V/√Hz。因此,1赫兹带宽下的输入参考点噪声电压 等于9.601×10⁻⁸ V。类似地,1兆赫和56.84兆赫的积分噪 声(带宽上的噪声)电压分别评估为9.601×10⁻⁵ V和9.601×√56.84 ≈ 72.38 ×10⁻⁵ V。根据(55),对应的噪 声功率分别为 −127.34dBm、 −67.34dBm和 −49.79 dBm。
归一化1赫兹噪声功率用于确定滤波器的动态范围。所提 出滤波器的1分贝压缩点评估为−1.5dBm,从而得到125.84分 贝的动态范围(DR)。同样,1兆赫和56.84兆赫带宽下的动 态范围(DR)分别计算为65.84分贝和48.29分贝。
表III展示了本工作与文献中报道的先进带通滤波器拓 扑的总结与比较。采用品质因数(FOM)来评估和比较带 通滤波器的性能。FOM越大,滤波器性能越好。根据设计 指标,文献中存在两种品质因数(FOM)的定义。第一种 计算方式为[3],[37]
$$
FOM_1 = \frac{P_{1dB}}{P_n \cdot P_{dc}}
$$
(56)
品质因数FOM的第二种定义由[11],[44],[45]给出
$$
FOM_2 = \frac{N \cdot P_{1dBW} \cdot f_{resonant} \cdot Q_{filter}}{P_{dc} \cdot NF}
$$
(57)
其中,N为极点数量,P1dBW为以瓦特为单位的带内1‐dB压 缩点,fresonant为谐振频率,Qfilter为谐振频率与3‐dB带宽之 比,Pdc为以瓦特为单位的直流功耗,NF为噪声系数(非 分贝值)。表III显示,所设计的滤波器达到的品质因数 FOM1为133.6dB‐Hz/mW,与Q增强型LC滤波器和开关 式Gm‐CN通路滤波器拓扑相比相当但略低。然而,所提出 的Gm‐C滤波器在低功耗、高品質因數、高通带增益、更小 的芯片面积和工艺可扩展性方面表现出更优的性能,但牺 牲了低动态范围DR。第二个品质因数FOM2 综合考虑了滤 波器的线性度、功耗、频率选择性和噪声性能,计算值为 94dB,是所有现有滤波器拓扑中最高的。
| 表II 有源带通滤波器的模拟噪声性能和动态范围 | |||||||
|---|---|---|---|---|---|---|---|
| P 1-dB (dBm) | 动态范围(dB) | ||||||
| 输入参考噪声功率(分贝毫) | 1-Hz 带宽 | 1兆赫 带宽 | 56.84兆赫 带宽 | ||||
| 点噪声@ 1‐Hz带宽 | 集成噪声@ 1‐MHz带宽 | 集成噪声@ 56.84MHz带宽 | P 1-dB (dBm) | ||||
| -127.34 | -67.34 | -49.79 | -1.5 | 125.84 | 65.84 | 48.29 |
| 表III 与先进有源带通滤波器拓扑的比较 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 参考文献(年份) | [46] (2002) | [47] (2003) | [3] (2003) | [37] (2005) | [48] (2006) | [11] (2006) | [45] (2008) | [38] 2013年 | [49] (2015) | This work |
| 技术 | 0.25微米 CMOS | 0.35微米 CMOS | 0.5微米 CMOS | 0.5微米 绝缘体上互补金属氧化物半导体 | 0.18微米 CMOS | 0.18微米 CMOS | 0.18微米 CMOS | 65纳米 CMOS | 40纳米 CMOS | 45纳米 CMOS |
| 滤波器阶数(N) | 6 | 2 | 2 | 2 | 3 | 4 | 2 | 4 | 8 | 2 |
| 谐振频率(GHz) | 2.14 | 2.19 | 0.9 | 2.5 | 2.368 | 2.03 | 2.44 | 0.4‐1.2 | 0.14 | 2.511 |
| ‐3dB带宽(MHz) | 60 | 53.8 | 20 | 70 | 60 | 130 | 60 | 21 | 7-56 | 36.21 |
| 品质因数 | 36 | 40 | 45 | 36 | 40 | 16 | 41 | 19‐57 | 3-20 | 69.34 |
| 中频增益(dB) | 0 | -13 | 11 | 23 | -1.8 | 0 | 6 | -3 | 0-20 | 72.76 |
| 电源电压(V) | 2.5 | 1.3 | 3 | 3 | 1.5 | 1.8 | 1.8 | 1.2/2.5 | 1.5 | ±1 |
| 功耗(mW) | 17.5 | 5.2 | 39 | 15 | 8.8 | 17 | 10.8 | 21.4 | 37.8 | 0.168 |
| 噪声系数(dB) | 19 | 26.8 | 21 | 6 | 18 | 15 | 18 | 10 | 34‐55 @gain=0dB | 29.62 |
| P1dB(dBm) | -13.4 | -30 | -5.5 | -15 | -20 | -6.6 | -15 | -4.4 | +12 @gain=0dB | -1.5 |
| 动态范围(dB‐Hz) | 142 | 117 | 137 | 153 | 135 | 152 | -160 | 131 | 125.84 | |
| 品质因数FOM 1 (dB‐赫兹/mW) | 129 | 110 | 121 | 141 | 125.6 | 140 | -146.4 | 115 | 133.6 | |
| FOM2(dB) | 72 | 49 | 67 | 82 | 78 | 77 | 81 | 85 | 45 | 94 |
五、版图后仿真与设计可扩展性
为了进一步检验所提出滤波器的性能并证明其新颖性, 本节进行了版图后仿真以及可扩展性分析。
A. 布局后仿真
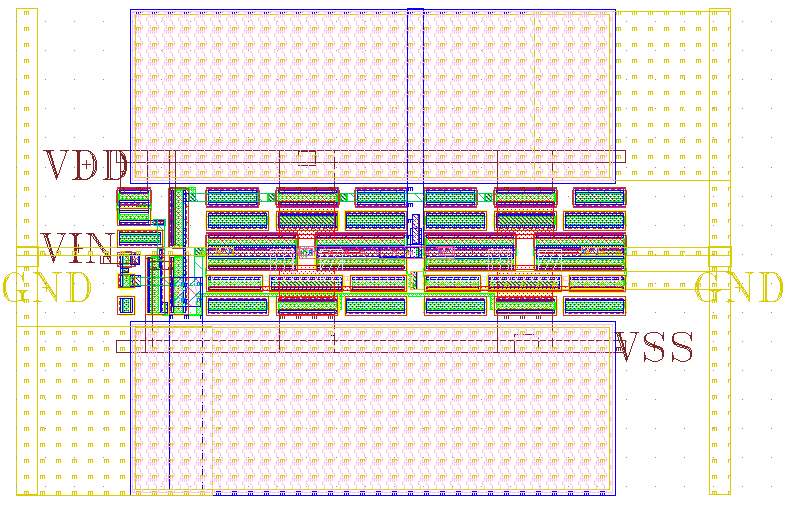
在45纳米技术节点上进行了完整的布局设计和提取仿 真,以验证该设计在工艺变化下的适用性和可靠性。所提 出的滤波器占据的有源面积为16.8μm × 24.6 μm。布局如 图10所示。
经过寄生参数提取后,所提出的滤波器的性能参数和 品质因数(FOM)与布局前仿真结果一致。FOM1和 FOM2分别计算为131.23dB‐Hz/mW和89.68dB。该滤 波器中心频率为2.43吉赫兹,具有46.2兆赫兹的3‐dB带宽, 品质因数为52.6。直流功耗和1‐dB压缩点分别为0.184毫瓦 和‐1.63dBm。在2.43吉赫兹处的噪声系数为30.11dB, 滤波器的动态范围(DR)为123.88dB。
B. 可扩展性
本工作获得的45纳米PTM结果通过使用台积电(台湾 半导体制造公司)的180纳米工业标准模型参数对提出的设 计进行仿真而得到验证。该验证方法与[50]‐[51]中采用的方 法一致。
采用±1 V的相同电源电压来获取所提出滤波器的设计 指标。该滤波器中心频率为2.51吉赫,实现3‐dB带宽为 54兆赫兹,品质因数为46.5,噪声系数为22.75分贝,1分 贝压缩点为2.53分贝毫瓦,功耗为0.388毫瓦。此外, 1‐Hz带宽下的点噪声为‐130.93分贝毫瓦,对应的动态范围 (DR)为133.46分贝赫兹。因此,上述参数得到的FO M1和FOM2分别为137.57分贝赫兹每毫瓦和97.57分贝。 可以看出,180纳米工艺节点下获得的FOM值与45纳米工 艺节点下的结果一致,验证了所提出设计在诸如45纳米等 超深亚微米CMOS技术中的可扩展性。
VI. 有源带通滤波器的可靠性
在本节中,研究了工艺、电压和温度(PVT)变化对 有源带通滤波器(BPF)电路设计指标的影响。这一点至 关重要,因为器件尺寸严格地缩小到纳米级,使得可靠且 考虑变化的模拟电路设计变得极具挑战性。此外,据我们 所知,此前尚未进行过对有源BPF拓扑的全面PVT分析。 本文特别重点考察了两个决定性参数:谐振频率(ω 0)和 总功耗(Ptot)。
A. 工艺变异性的影响
由于金属氧化物半导体(MOS)器件的持续微型化, 工艺变异性对电路性能产生了严重影响。通常,超大规模 集成电路(VLSI)器件和电路中的变异性源于晶圆制造工 艺步骤中的随机变化,这些变化包括芯片间和芯片内因素 [52]。因此,任何参数x的总体偏差为
$$
\sigma_x = \sqrt{\sigma_{x,\text{interdie}}^2 + \sigma_{x,\text{intradie}}^2}
$$
(58)
为了验证设计对工艺失配的鲁棒性,已进行了蒙特卡 洛和角点仿真。
1) 仿真设置
工艺变异性的主要来源包括对工艺敏感的设计参数, 如沟道长度L、沟道宽度W、栅氧化层厚度tox、掺杂浓度 NCH等。在深亚微米CMOS技术中,随机掺杂波动(RDF)、 线边粗糙度(LER)、线宽粗糙度(LWR)、金属栅功函数波 动(WKF)和氧化层厚度变化(OTV)是内在变异性[52],[53] 的主要来源。
为了建模工艺波动的影响,假设工艺/器件参数(如L、 W、tox和NCH )具有独立的高斯分布,其变化范围为国际 半导体技术路线图(ITRS)指南[54]预测的 ±10%。通过在 45纳米技术节点下改变上述参数生成不同的模型文件,并 进一步估算关键的设计指标。此外,所有参数的影响可转 化为对阈值电压Vt的关联性影响。由于波动分量的统计独 立性,Vt的总变化(σVt,total)可近似表示为[53]
$$
\sigma_{V_{t,\text{total}}} \approx \sqrt{ (\sigma_{V_{t,\text{RDF}}})^2 + (\sigma_{V_{t,\text{WKF}}})^2 + (\sigma_{V_{t,\text{PV}}})^2 }
$$
(59)
其中,Vt,WKF和Vt,PV分别为由功函数波动和工艺变化引起 的器件阈值波动。同样,σVt,RDF为由于RDF引起的波动分 量,其值等于[55]
$$
\sigma_{V_{t,\text{RDF}}} = \frac{q \sigma_N \sqrt{N_{CH} t_{ox}}}{4 \sqrt{3} \varepsilon_{Si} \varepsilon_{ox} W_{eff} L_{eff}}
$$
(60)
其中,NCH为沟道掺杂浓度,Leff和Weff分别为有效沟道长 度和宽度,q为电子电荷q,εSi和εox分别为硅和SiO2的介 电常数,tox为氧化层厚度。此外,Vbi为源/漏到沟道的 pn结的内建电势。
因此,仅需在阈值电压[56]上应用具有 ±10%变化的 3σ高斯分布,即可捕捉到相同的效果。
2) 蒙特卡洛采样
进行了5000次迭代的蒙特卡洛仿真,通过对前述器件 参数应用高斯分布,并估计了设计指标ω 0 和Ptot 。这些变 化的整体效应可使用与电流因子(β)相关的Pelgrom方程 [56]来描述。
$$
\sigma_\beta^2 = \frac{\sigma_{C_{ox}}^2}{C_{ox}^2} + \frac{\sigma_{\mu_n}^2}{\mu_n^2} + \frac{\sigma_L^2}{L^2} + \frac{\sigma_W^2}{W^2} + \frac{\sigma_{C_{ox}}^2}{C_{ox}^2}
$$
(61)
对于深亚微米CMOS技术,当电场超过临界电场(Ec)时, 载流子迁移率(μn)趋于饱和,并且对 β的变化贡献极小。
利用佩尔格罗姆定律,可确定任意参数P的方差∆P
$$
(\Delta P)^2 = \left( \frac{A_p}{WL} \right) \sigma^2 + \left( \frac{S_p D_x}{WL} \right)^2
$$
(62)
这里,P的面积和间距比例常数分别用Ap和Sp表示,Dx 是匹配器件之间的间距。
由(62)式,ω0和Ptot变化的广义表达式可建模为
$$
\sigma_{\omega_0}^2 = \sum_i \left( \frac{\partial \omega_0}{\partial x_i} \right)^2 \sigma_{x_i}^2
$$
(63)
$$
\sigma_{P_{tot}}^2 = \sum_i \left( \frac{\partial P_{tot}}{\partial x_i} \right)^2 \sigma_{x_i}^2
$$
(64)
其中,σxi是第ith个器件的器件参数x的标准偏差。
表IV比较了提出的设计在ω 0 方面的变异性与文献中 报道的一些基于VDTA的有源带通滤波器的变异性。此外, 还考察了未采用负阻网络的传统CMOSVDTA实现的所设 计滤波器的可靠性。可以看出,所报道的变异性在之前发 表的所有设计中是最小的,从而验证了提出的设计的可靠 性。同样,表五突出了所提出的滤波器相较于文献中其他 有源和无源带通滤波器拓扑在可靠性方面的提升。
| 表IV 基于VDTA的有源带通滤波器拓扑结构中谐振频率变化性的比较 | |||||
|---|---|---|---|---|---|
| 参考文献 (年份) | 样本数量 (N) | 标准偏差(σ) | 均值(μ) | 变异性 (σ/ µ) | 应用于器件的变化百分比 参数和电路元件 |
| 57 | 500 | 6.656千赫 | 1.009兆赫 | 0.0066(18.33×) | 器件参数5%变异和器件阈值10%变异& 器件阈值10%变异 |
| 58 | 100 | (a)33.73千赫 (b)103.45千赫 | (a)3.08兆赫 (b)3.09兆赫 | (a)0.011(30.55×) (b)0.033(91.66×) | (a)器件参数的5%变化 (b)电容值的5%变化 |
| 31 | 100 | (a)29.30千赫 (b)105.28千赫 | (a)3.092兆赫 (b)3.09兆赫 | (a)0.0095(26.38×) (b)0.034(94.44×) | (a)器件参数的5%变化 (b)电容值的5%变化 |
| 59 | 100 | 292.424千赫 | 7.204兆赫 | 0.041(113.88×) | 电容的10%变化 |
| 60 | 100 | 17.8千赫 | 3.98兆赫 | 0.004(11.11×) | 电容的10%变化 |
| 传统的 VDTA | 5000 | 3.16兆赫 | 2.769吉赫 | 0.00114(3.56×) | 器件参数和电容的10%变化 器件参数和电容的10%变化 |
| 本工作 | 5000 | 813.93千赫 | 2.51吉赫 | 0.00032 | 器件参数和电容的10%变化 参数与电容 |
| 表五 谐振频率变异性与其他有源和无源带通滤波器拓扑结构的比较 | |||||
|---|---|---|---|---|---|
| 参考文献 (年份) | 样本数量 (N) | 标准偏差(σ) | 均值(μ) | 变异性 (σ/ µ) | 应用于器件的变化百分比 参数和电路元件 |
| 61 | 100 | 2.4兆赫 | 40兆赫 | 0.06(187.50×) | − |
| 62 | 200 | 1.175千赫 | 24.95千赫 | 0.047(146.87×) | − |
| 63 | 20 | 11千赫 | 2.009兆赫 | 0.0054(16.87×) | 来自20个测试芯片的数据 |
| 64 | 100 | 26.33千赫兹 | 1.102兆赫兹 | 0.023(71.87×) | 电阻5%变化&10% 电容变化 |
| 65 | 200 | 10千赫兹 | 1.6兆赫兹 | 0.00625(19.53×) | 电阻5%变化 |
| 66 | 200 | (a)33.35千赫 (b)530.611 | (a)1.66兆赫 (b)1.67兆赫 | (a)0.02(62.50×) (b)0.00031(0.96×) | (a)电容值的5%变化 (b)gm‐值的5%变化 |
| 67 | 1000 | (a)2.259千赫 (b)197.43千赫 | (a)1.65兆赫 (b)1.69兆赫 | (a)0.0013(4.06×) (b)0.116(362.50×) | (a)gm值的20%变化 (b)电阻的20%变化 |
| 68 | 1000 | 1.5GHz | 60GHz | 0.025(78.12×) | − |
| 69 | 10000 | 2GHz | 77GHz | 0.026(81.25×) | MIM电容的10%变化 |
| 70 | 40 | (a)96.12兆赫 (b)20.16兆赫 | (a)5.4吉赫 (b)2.8吉赫 | (a)0.0178(55.62×) (b)0.0072(22.25×) | 来自40个测试芯片的L g ate=数据 (a)0.2微米(b)0.4微米 |
| 本工作 | 5000 | 813.93千赫 | 2.51吉赫 | 0.00032 | 器件的10%变化 参数和电容 |
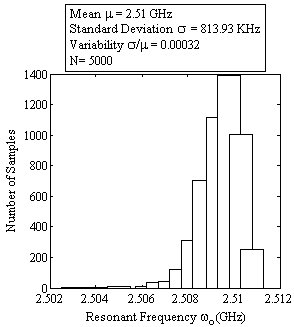
谐振频率(ω0)和总功耗(Ptot)的良率分布分别如图11和 图12所示。可以看出,谐振频率在均值(μ)2.51吉赫附近 的标准偏差(σ)为813.93千赫,由此产生的变异性(σ/μ) 为0.00032。谐振频率的更窄分布意味着带通滤波器其他 设计指标(如品质因数Q和3‐dB带宽(BW))的分布也 更窄,从而验证了该设计具有抗变异性能力。
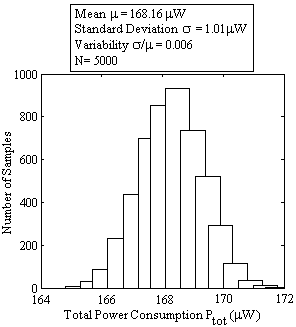
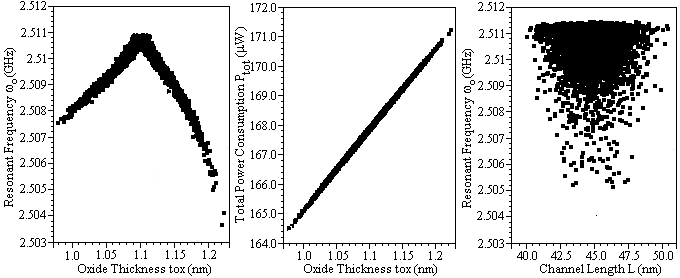
同样,对于Ptot,其标准偏差、均值和变异性分别为 1.01μW、168.16μW和0.006。图13显示了5000个样本的 ω 0 和Ptot 的散点图,对应于氧化层厚度tox 和沟道长度L的 变化。
3) 工艺角分析
在CMOS工艺流程中,除了NN(标称)工艺角外,还 定义了4种工艺角,即SS(慢‐慢)、FF(快‐快)、FS (快‐慢)和SF(慢‐快)。它们分别对应NMOS和P MOS晶体管快慢组合的情况。慢速器件意味着更厚的栅氧 化层、更高的器件阈值以及降低的载流子迁移率,这会导 致在相同栅极驱动下漏极电流减小。
相反,快速器件意味着更薄的栅氧化层、更低的器件阈值和更高 的载流子迁移率,这会导致在相同的栅极驱动[71]下漏极电流增加。
有源带通滤波器的设计指标在所有五个工艺角下进行 了估算,并列于表VI中。从表VI可以看出,FS和SF角的设 计指标分别与FF和SS角的基本相同。
| 表VI 有源带通滤波器在5种工艺角下的仿真设计指标 | |||||
|---|---|---|---|---|---|
| 参数 | NN | FF | SS | SF | FS |
| ω 0 ( 吉赫兹 ) | 2.511 | 2.518 | 2.085 | 2.086 | 2.517 |
| P tot ( μW ) | 168.12 | 171.43 | 164.58 | 164.61 | 171.41 |
B. 电压和偏置电流变化的影响
为了估计ω0和Ptot对电源电压和偏置电流的依赖性, 在VDD和Ibias的标称值附近施加10%变化,并观察ω0和Pdis 的相应变化。结果分别如图14和图15所示。
如所观察到的,有源带通滤波器消耗的功率随着VDD和Ibias的 增加而线性地增加。Ptot相对于VDD和Ibias的灵敏度可近似为
$$
S_{P_{tot}/V_{DD}} = \frac{\Delta P_{tot}}{P_{tot}} \cdot \frac{V_{DD}}{\Delta V_{DD}}
$$
(65)
$$
S_{P_{tot}/I_{bias}} = \frac{\Delta P_{tot}}{P_{tot}} \cdot \frac{I_{bias}}{\Delta I_{bias}}
$$
(66)
类似的表达式也可用于确定谐振频率(ω 0)的灵敏度。 如前所述,偏置电流(Ibias)可用于电子调节VDTA参数, 例如ω 0 ,从而调节所提出的有源BPF的其他设计指标,如 Q值、3‐dB带宽等。
C. 温度对可靠性的影响
器件阈值(Vt)和载流子迁移率(μ N )的热不稳定性 对纳米级集成电路的性能和可靠性有显著影响。这些变化 是由于环境温度波动和/或MOS晶体管功耗引起的。芯片中 的功耗导致全局以及局部温度波动。局部变化通常出现在 高活动区域,称为“热点”,而芯片温度的全局偏移则是 由环境/环境温度变化[72]引起。因此,芯片内部的温度并 非恒定,从而导致集成电路性能的变化。在纳米尺度范围 内,由于尺寸不断减小,上述现象更加严重 电源电压和阈值电压之间的差异。这使得将设计指标限制 在给定范围内变得极具挑战性。
阈值电压Vt表现出对温度的线性依赖性,可以建模为[73]
$$
V_t(T) = V_t(T_0) + \alpha_{Vt} (T - T_0)
$$
(67)
这里, αVt是阈值电压温度系数,T0是参考温度( 300K)。假设阈值电压温度系数为常数,其取值范围为 −1 mV/°C到−4 mV/°C,最常用的数值为 −2 mV/°C[74]。
同样,已知迁移率对温度呈指数依赖性,即[74]
$$
\mu_N(T) = \mu_N(T_0) \left( \frac{T}{T_0} \right)^{\alpha_\mu}
$$
(68)
其中,α µ 是迁移率温度指数,与α Vt一样也是一个提取参数。 通常,αµ被近似为
$$
\alpha_\mu = \alpha_{\mu0} + \alpha_{\mu1} \left( \frac{T - T_0}{T_0} \right)
$$
(69)
对于n沟道器件,µ0和µ1均为负值,分别位于 −2.1到 −1.9 以及 −0.05到 −0.01的范围内[75]。然而,出于建模目的, αµ被视为常数。由(67)和(68)可知,迁移率和阈值电压均 表现出负的温度依赖性。当温度升高10




















 972
972

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








