博弈论视角下的环境投资合作

对我有什么好处？——通过博弈论视角分析环境投资

1 引言

环境投资通常旨在实现双赢局面，使企业能够同时实现生态和经济目标。如果没有积极的经济效应，这些投资从长远来看将难以被接受，从而导致负面环境影响。这些投资往往需要大量资金，因此公司不得不通过合作来分担财务负担和风险。

此类合作对环境以及对企业产生的积极影响已在多项研究中得到强调（布恩斯和扬森，2004；达沃斯和拉贾诺，2001；费伦霍夫等，2014；任等，2014；苏林和穆勒，2007）。除了创造生态经济双赢局面外，此类合作的主要目标是为所有合作伙伴实现纯粹的经济双赢局面。他们希望以一种能够获得优于各个体收益之和的方式达成既定目标，从而形成所谓的协同增益。例如，该目标可能包括降低投资成本、改善工作负荷、更好地利用残余物和/或优化定制化的网络连接（雅各布森，2006；舒伯特，2007年，第150页）。协同增益必须以一种使合作成为企业最佳选择的方式来分配。

在这种分配方式下，公平分配的问题便随之产生。“在任何合作中，关于每个企业应贡献多少以及利润如何分配的规则都难以确立。每个企业可能都会认为自己比其他企业贡献更多......”（Tripsas 等，1995年，第371页）。只要在此背景下“公平性”的定义尚不明确，就无法对合作的结果进行评估。尽管合作行为在环境管理中被广泛接受，但公平分配问题在文献中却鲜有关注。仅有少数研究（赫尔姆，2000；卡尔佩里斯等，2013；卢等，2014；莫雷蒂，2004；蒂斯和布兰泽伊，2004）建议将合作博弈论引入环境管理。这些研究仅局限于讨论核心和/或夏普利值。

为克服这些不足，本文的目的有三。首先，我们将讨论环境管理决策中合作的含义和形式。其次，我们将介绍并分析合作博弈论的基本性质。第三，我们将介绍不同的解概念，并讨论其性质和实用性。关于合作在环境管理中作用的讨论将在下一章中提供。

2 环境管理与博弈论中的合作

2.1 合作在环境管理中的作用

合作是指至少两个独立公司之间通过合同约定的自愿协作。在下文讨论中，协作的强度和范围并不重要。多种协作形式均可归类为合作，例如纵向、横向或联合企业合作、战略联盟和/或网络。合作的好处可能包括成本降低、收入增加、风险降低、减少环境污染和/或形象改善（费伦霍夫等，2014，第50页；格列科娃等，2014年，第175页；希佩尔等，2011年，第6874–6878页；雅各布森和安德伯格，2004年，第319–321页；卢等，2014，第349–350页）。就利益的产生和/或分配而言，可以区分出三种类型的合作：

收益的隐性生成 ：合作的收益在不同企业中隐性产生，并未公开披露。所有合作者均认为他们能从合作中受益。该效应可用一个总和来量化（雅各布森和安德伯格，2004，第314–326页），但未讨论合作伙伴之间的公平性。在此背景下，合作被认为比独立方案能带来更好的结果。

收益的隐性分配 ：企业间的相互依赖要求使用并量化转移价格。这些价格可能包含合作收益的分享，例如在战略联盟中。公平的利益分配问题不一定显而易见。

收益的显性分配 ：企业被强制计算、披露并划分共同产生的收益。这在合资企业中是一种标准程序。在此背景下，公平的利益分配问题至关重要，并且潜在合作伙伴在建立合作之前会对此进行深入讨论。

再利用和回收网络是收益的隐性生成的典型代表。这些网络提高了产能利用率，降低了采购价格，并导致物料流量的均质化和连续性程度提高。所有这些效应都会显著减少环境污染和成本（卡马林哈‐马托斯和阿布鲁，2007年，第595页；雅各布森，2006年，第250–253页）。

“此外，有观点指出，技术合作在成功时会产生超可加性收益；应将其视为一种正和博弈”（德布雷松和阿梅斯，1991年，第368页）。鉴于实际考虑，在环境管理背景下，成本与收益的公平分配问题并未被频繁探讨。这是因为从企业的角度来说，合作所产生的效益是单独行动无法实现的。这意味着独立选项不如合作有效。

环境技术投资是具有明确收益分配的合作的典型例子，因为投资金额将在合作伙伴之间进行分摊。投资金额越高，现金转换周期越长，企业寻求联合解决方案（例如构建网络）的意愿就越强。该网络中不同企业的联合投资将产生不同的结果。这种合作形式构成了以下分析的核心。联合投资的成本低于各企业单独投资成本的总和，这是合作的主要动力。然而，问题在于如何在合作伙伴之间分享这一收益。

这种情况可被视作企业（称为参与者）之间的合作博弈。为了分析此类情形，下一部分将重点阐述合作博弈的主要特征。

2.2 合作博弈及其特性

合作博弈的特点在于参与者可以达成固定的有约束力的协议，并且能够相互协调其行为。另一个需要进一步考虑的特征是联盟产生的收益是完全可转移的。也就是说，该收益可以全部分配给那些为产生收益做出贡献的联盟成员。因此，在博弈论中，联盟成员之间的转移支付成为可能，这种支付被称为侧向支付。

合作博弈 Γ 由一个参与者集合 N ={1,2,…,n} 组成。在此，不仅所有参与者的数量 N 很重要，N 的所有子集也同样重要。这样的子集 S⊆N 称为联盟 S，其中 N 本身被称为大联盟。公平分配协同效应的基础是博弈的特征函数，该函数对每个联盟 S 标记一个值 v(S)（冯·诺依曼和摩根斯特恩，1947，第 238页）。函数 v 为每个子集 S 分配一个值，表示该联盟的经济绩效。空联盟的结果为零，因此 v(∅)=0。成本降低博弈的特征函数基于成本函数 c(S)，因此该博弈 Γ 由 Γ(N, c) 定义。博弈的特征函数基于该博弈的成本函数推导得出（杨，1994，第1206–1217页）。

定义1 ：合作博弈 Γ（N, v）的特征值函数 v: 2^N → R 基于成本函数 Γ（N, c）计算如下：v(S) = ∑_{i∈S} c({i}) - c(S), ∀ S ⊆ N。

仅关注由于成本降低而具有超可加性特征函数的博弈。多家企业共同投资并安装设备，其成本低于各自单独购置设备成本之和，这一事实通过成本的次可加性特征予以考虑（蒂斯和德里斯森，1986年，第1016页；杨，1985年，第66页）。在假设收入固定的情况下，成本的次可加性导致特征函数的超可加性。

性质1 ：具有可转移效用的特征函数 v 是一个超可加性函数，如果对于所有联盟 R,S ⊆ N，当 R 与 S 不相交时，满足：v(R) + v(S) ≤ v(R ∪ S)。

此外，必须要求新增的参与者不会损害联盟的利益。这被称为单调性。

性质2 ：博弈 Γ(N, v) 具有单调性，如果对于 v(S) ≤ v(R), ∀ S ⊆ R ⊆ N 成立。

此外，如果大联盟产生的结果优于所有独立联盟的结果之和，则更为理想。如果一个博弈满足这一要求，则该博弈称为本质博弈。

性质3 ：一个博弈 Γ(N, v) 是本质的，如果 v(N) > ∑_{i∈N} v({i})。

此外，必须指出的是，较大的联盟比小型联盟能产生更好的结果。这被称为凸性。

性质4 ：博弈 Γ(N, v) 是凸的：
- 如果对于所有联盟 R, S ⊆ N，既不满足 R ⊆ S 也不满足 S ⊆ R：v(R ∪ S) + v(R ∩ S) ≥ v(R) + v(S)
- 或者对于所有联盟 R, S ⊆ N 其中 S ⊆ R，以及对于每个既不属于 S 也不属于 R 的参与者 i ∈ N，满足：v(S ∪ {i}) - v(S) ≤ v(R ∪ {i}) - v(R)

这些性质描述了合作博弈的特征。需要指出的是，这些性质仅构成基础，除此之外还可区分其他性质。其中一些性质将在后续章节中讨论。

3 解的概念

3.1 一般公理

解的一个基本要求是满足个体理性。当且仅当分配的仅为所产生的协同利润时，该解是符合个体理性的。此外，必须确保没有任何可能的联盟会被单企业联盟所阻挠，即不存在否决权。

公理1（个体理性） ：对于联盟函数 v 的支付向量 x=(x₁, x₂,…xₙ)，必须满足 ∑_{i∈N} xᵢ ≤ v(N)，并且对所有参与者 i ∈ N 成立：xᵢ ≥ v({i})。

除了个体理性之外，还必须确保由帕累托效率描述的集体理性。

公理2（集体理性） ：在帕累托有效解中，如果不恶化另一家公司的处境，就无法改善任何一家公司的处境。因此 ∑_{i∈N} xᵢ ≥ v(N)。

通过这两个公理，博弈的可能解被限制在分配集范围内。一个分配描述了所产生利润的分配方式，这种分配是个人理性和集体理性的（亨内特，2010年，第114页；冯·诺依曼和摩根斯顿，1947年，第34页）。

定义2 ：满足这些条件的解称为分配，因此由 ∑_{i∈N} xᵢ = v(N) 以及 xᵢ ≥ v({i}), ∀ i ∈ N。

作为进一步的要求，必须指出，不向联盟出资的公司也不会获得联盟利润的份额，因为该联盟在没有这家公司的情况下也能产生相同的利润（蒂斯和德里斯森，1986年，第1016页）。

公理3（虚拟参与者） ：如果一家公司对任何可能联盟的边际贡献均为零，则该公司为虚拟参与者。该参与者 i 满足 v(S ∪ {i}) = v(S) + v({i}), ∀ S ⊆ N \ {i}。该公司 i 的分配份额为 xᵢ = v({i}) = 0。

除了这一要求外，还要求对利润贡献相同的两家公司应受到同等对待（对称性）。公司在分配收益时的标签并不重要。

公理4 (对称性) ：对于两家公司 i 和 j，其中 i,j ∉ S 且满足 v(S ∪ {i}) = v(S ∪ {j}), ∀ S ⊆ N \ {i,j}，其收益必须满足 xᵢ = xⱼ。

在考察形成联盟的多种可能性时，必须指出，不可能通过将一个博弈拆分为两个博弈来获得更好的结果。这一点由可加性公理所表达，因为两个博弈的解相加所产生的结果必须与这两个博弈之和的解相同（聚合定律）（沙普利，1953年，第309页）。

公理5（可加性） ：如果参与者 i 参与两个具有收益函数 v 和 w 的博弈，则对于每个参与者 i ∈ N，其在 v+w 中的收益必须等于单个博弈 v 和 w 收益之和：xᵢ(v + w) = xᵢ(v) + xᵢ(w)。

公平解的另一个理想特性是，合作成果的增加会导致合作伙伴的收益增长。这一原则被称为总体单调性，似乎是公平分配的一个普遍原则，因为它指出，当问题的基础数据发生变化时，解应以相应的方式发生变化（杨，1985，第65页）。该原则表明，如果大联盟的价值增加，而所有其他联盟的价值保持不变，则任何参与者都不应比之前获得更少的收益（杨，1985，第66页）。

公理6（单调性） ：若对于博弈 Γ₁（N，v）和 Γ₂（N，w），其分配方案的收益满足 v(N) ≥ w(N) 且 v(S) = w(S), ∀ S ⊆ N 时，有：xᵢ(v) ≥ xᵢ(w), ∀ i ∈ N。

单调性公理对于解能否为参与者创造激励至关重要。当且仅当联盟价值的增长为各参与者带来的份额不低于增长前的水平时，该解才是公平的。

基于这些基本要求，近年来已发展出多种解概念（综述参见 Fiestras‐Janeiro 等, 2011）。在这些概念中，以下章节仅介绍核心、夏普利值、核仁和τ‐值。

3.2 核

为了解决分配问题，唯一值得关注的分配是那些不被其他分配所支配的分配，因为只有不被支配的分配才包含加入联盟的激励。不被支配的分配集构成核心（Arin 和 Feltkamp, 2012, 第209页；Gillies, 1959；Moulin，1988，第94–95页）。具体而言，博弈的核心是指任何（但非更大）联盟都无法阻挠的分配集（Gilles, 2010, 第36页；刘, 2009, 第225页）。

定义3 ：对于一个合作博弈 Γ(N,v) 的核心 C(N,v) 由所有不被支配的分配组成，因此可得 C(N,v) = {x | ∑_{i∈S} xᵢ ≥ v(S), ∀ S ⊆ N}。

合作博弈的核心包含所有公平且因此稳定的解。核心可能很小，也可能非常大，或者是空的。凸博弈的核心从不为空（Shapley，1971年，第24页）。但非凸性并不是存在非空核心的充分条件。对于一个非凸博弈，仍有可能存在核心。因此，另一类博弈变得相关——即所谓的平衡博弈。为了定义一个博弈的平衡性，使用一个向量 z_S(i) 来描述参与者 i 是否属于联盟 S，其规则如下：
z_S(i) = 1 if i ∈ S, else 0.

基于博弈的特征函数，可以形成一个非空的联盟子集 Ψ，其中 Ψ = {S₁, S₂, …, S_m}，并引入权重因子 α_j，其中 j = 1, …, m（德里斯森，1988年，第47页；贾因和马赫迪安，2007年，第388页）。

性质5 ：一个博弈的子集 Ψ = {S₁, S₂, …, S_m} 被称为平衡的，如果对于所有参与者 i ∈ N，存在实值系数 α_j > 0，使得 ∑_{j: i ∈ S_j} α_j = 1, ∀ i ∈ N。

基于博弈子集的平衡性，可以验证一个博弈的平衡性。

性质6 ：博弈 Γ(N,v) 是平衡的，如果对于所有平衡子集 Ψ 且 α_j > 0，均有 ∑_{j=1}^m α_j v(S_j) ≤ v(N)。每个平衡博弈都具有非空核心（邦达列娃，1963年；沙普利，1967年）。核心作为一种解概念，并不提供关于如何分配协同效应的具体建议，但它可以判断是否存在一个稳定解甚至一组稳定解。在环境管理的背景下，核心常被用作理性论证的基础（菲努斯，2001年，第246–248页；赫尔姆，2000年，第70–76页；卢等，2014年，第351–355页）。

3.3 夏普利值

要确定夏普利值，边际贡献的概念至关重要。参与者的边际贡献是指其加入联盟所引起的价值增加。

定义4 ：参与者 i 对于联盟 S ⊆ N 的边际贡献 mc_{i;S}(v) 由 mc_{i;S}(v) = v(S ∪ {i}) - v(S \ {i}) 确定。

该参与者在不同联盟中的边际贡献 mc_{i;S}(v) 会表现出不同的值。考虑到形成联盟的不同方式，可能存在 n! 种序列，因此每位参与者都有 n! 个边际贡献值。假设所有顺序的概率相同，则每位参与者的边际贡献之和将根据可能的顺序数量进行加权。

定义5 ：参与者 i 的加权边际贡献 ϕ_i(v) 结果为
ϕ_i(v) = ∑_{S ⊆ N{i}} [ |S|!(n-|S|-1)! / n! ] × [v(S ∪ {i}) - v(S)]

这个加权和以其提出者劳埃德·S·沙普利（沙普利，1953年，第311页）的名字命名，称为夏普利值。夏普利值是最重要的单值解概念之一，已被多次用于一般情况下的公平成本分摊（哈姆伦等，1980年；马施勒等，2013年，第748页；冈本，2008年；铃木和中山，1976年），以及环境管理中的问题（博特翁和卡拉罗，1998年；赫尔姆，2000 年，第76–78页；卡尔佩里斯等，2013年，第1298页；张等，2014年）。夏普利值的主要问题是，它仅在凸博弈中始终属于非空核心（沙普利，1971年，第29页； Sudhölter 和 Peleg，1998年，p.386）。如果该博弈是非凸的，则夏普利值可能不属于核心——在这种情况下，它不是一个稳定且公平的解决方案。由于该值易于计算且广为人知，因此在非凸博弈的情况下，存在被误解和误读的风险。

3.4 核仁

核仁是另一个著名且重要的解，由施迈德勒（1969年）提出。在计算该值时，关键概念是不满意。不满意指的是联盟对某一具体支付向量的不满程度，在此背景下被称为超额（Driessen，1988，第37–38页；Kruś 和 Bronisz，2000，第263页； Moulin，1988，第121–123页）。

定义6 ：联盟 S 关于支付向量 x 的超额 ex(S, x) 由 ex(S, x) = v(S) - ∑_{i∈S} xᵢ。

联盟对支付向量的不满意程度是关注的核心。通过最小化每位参与者的最大不满，生成核仁。为此，下一步需找出每位参与者具有最高不满意的支付向量。这通过将这些抱怨向量按降序排列来实现，即从最大值开始排列。

定义7 ：超额值的字典序 Θ(x) = (ex(S₁,x), ex(S₂,x), …, ex(S_N,x)) 按如下方式构造：ex(S_j,x) ≥ ex(S_{j+1},x), ∀ j = 1, …, N-1。

这些向量按字典序排列。

定义8 ：如果比较两个分配 x 和 y，则称 x 字典序更小 ≺_L 于 y，如果存在一个索引 m，使得 (a) Θ_k(x) = Θ_k(y), ∀ k < m 且 (b) Θ_m(x) < Θ_m(y)。

按字典序最小的分配定义了该过程的解。由于此分配最小化了所有参与者的不满意程度，因此它定义了核仁。

定义9 ：在博弈 Γ（N，v）中，核仁 nuc（v）关于分配集 I（v）定义为：nuc(v) = {x ∈ I(v) | Θ(x) ≺_L Θ(y), ∀ y ∈ I(v)}。

核仁在博弈论领域已有充分研究（马施勒等，2013年，第801–816页），但在环境管理领域却未受到关注，与夏普利值形成对比。

3.5 τ-值

τ‐值是一个较新的概念（Driessen，1983，1988年；Driessen 和 Tijs，1982；Tijs 和 Driessen，1986；Tijs，1981），但其在解决管理问题方面的应用却很少（Jene 和 Zelewski，2011；Zelewski 和 Peters，2010年）。

τ-值的概念定义了两个向量：上向量和下向量。这些向量是从参与者角度来看他们可能达到的最佳情况（上限）或最少情况下可获得的界限。

（下限）。上限由参与者对大联盟的边际贡献决定。

定义10 ：在n人博弈 Γ(N，v)中，向量 b 由 b_i = v(N) - v(N{i}) 定义，称为上向量。

除了参与大联盟外，任何参与者都有可能组成并运作一个外部联盟。公司 i 会理性地追求这样一个联盟：在该联盟中，其自身收益与其他公司为加入该外部联盟所需支付的侧向支付之间的差额达到最大（Curiel, 1997, 第1页；Tijs, 1981, 第2‐3页）。

这一最大值代表了下限——也称为威胁点或让步极限。

定义11 ：在n人博弈Γ（N，v）中，向量 a，其定义为 a_i = max_{S ⊆ N{i}} [v(S) - ∑_{j∈S} b_j]，被称为下向量。

向量 a 和 b 不一定代表分配。如果在这两个向量之间应存在一个分配，则必须引入以下条件：

性质7 ：一个n人博弈Γ(N, v)是拟平衡的，如果满足以下条件：∑ {i∈N} a_i ≤ v(N) ≤ ∑ {i∈N} b_i。对于拟平衡博弈，存在一个明确确定的分配，该分配位于上向量和下向量之间，被称为τ‐值（Tijs, 1981, 第5‐8页；Tijs, 1986, 第4页）。

定义12 ：拟平衡博弈 Γ(N, v) 的 τ‐值由 τ(v) = a + λ(b - a) 定义，其中 λ = 0 若 a = b，否则 λ = [v(N) - ∑ {i∈N} a_i] / [∑ {i∈N} (b_i - a_i)]。

与夏普利值相比，τ‐值的优势在于，其概念比所有联盟形成序列等概率的假设更接近现实。通过定义上限和下限，参与者的机遇得以更贴近企业决策过程的方式体现出来。公司要么加入大联盟，要么组成外部联盟。而夏普利所提出的检验并计算所有可能的联盟形成顺序的思路，并不那么令人信服。

τ‐值尚未被用于解决环境管理中的公平分配问题。

4 示例说明

4.1 初始情况

我们正在分析三家被要求安装澄清能力的企业的情况。这些公司预测的年污水量如下：公司A和C各自产生1500百升（hl），公司B产生1000百升。不同可行方案的技术和财务参数如表1所示。

表1 不同污水处理厂的信息

设备规模	年产能 [百升]	总成本 [€]	特定成本 [€/hl]
小型	1500	150,000	100.00
中型	2500	220,000	88.00
大型	3000	250,000	83.33
合作企业	4000	340,000	85.00

在这种情况下，提出了以下问题：从经济角度而言，哪种类型的设备是最有效的，以及如何分摊成本。

一种可能的解是合作设备的平均分配，这样每家公司都需承担113,333.33欧元的成本。但从公司B的角度来看，这并不公平，因为该公司仅产生全部污水量的25%。

另一种方案是根据按因分摊成本原则对合作设备进行成本分摊。公司A和C各自需支付127,500欧元，而公司B只需支付85,000欧元。然而，这种方案面临的问题是，公司A和C有可能选择相互合作，仅安装一套大型设备，投资成本为250,000欧元。与独立解决方案相比，这将使每家公司的投资成本减少25,000欧元。该替代方案的单位成本为每百升83.33欧元，相较于合作设备更为便宜。因此，从公司A和C的角度来看，按照按因分摊成本原则，它们没有动力与公司B合作。为解决这一问题，下文将采用上述合作博弈论的机制。

4.2 通解的识别

根据输入信息，推导出该情境下的成本函数，如表2所示。该函数不能作为特征函数使用，必须转换为成本缩减函数。

表2 污水处理厂的成本函数（单位：千欧元）

S	{∅}	{A}	{B}	{C}	{A,B}	{A,C}	{B,C}	{A,B,C}
c(S)	0	150	150	150	220	250	220	340

首先，必须明确通过形成不同联盟所能实现的成本降低。这通过定义1完成，并得出成本降低的函数，如表3所示。

表3 成本降低博弈的函数（单位：千欧元）

S	{∅}	{A}	{B}	{C}	{A,B}	{A,C}	{B,C}	{A,B,C}
v(S)	0	0	0	0	80	50	80	110

这是成本降低博弈的特征函数，可作为使用合作博弈论解概念的基础。通过证明不同的性质，可以得出该博弈是
* 超可加性（参见第4页的性质1）
* 单调性（参见第4页的性质2）
* 本质的（参见第4页的性质3）
* 非凸的（参见第5页的性质4）。

由于该博弈是非凸的，因此可能存在稳定解不存在的情况。因此，使用性质6来验证博弈的平衡性。可以得出结论：该博弈是平衡的，因此存在非空核心。根据定义3生成该博弈核心存在性的约束条件：
$$
\begin{cases}
x_A, x_B, x_C \geq 0 & \text{个体理性} \
x_A + x_B + x_C = 110 & \text{集体理性} \
x_A + x_B \geq 80 & \
x_A + x_C \geq 50 & \text{阻挠分配。} \
x_B + x_C \geq 80 &
\end{cases}
$$
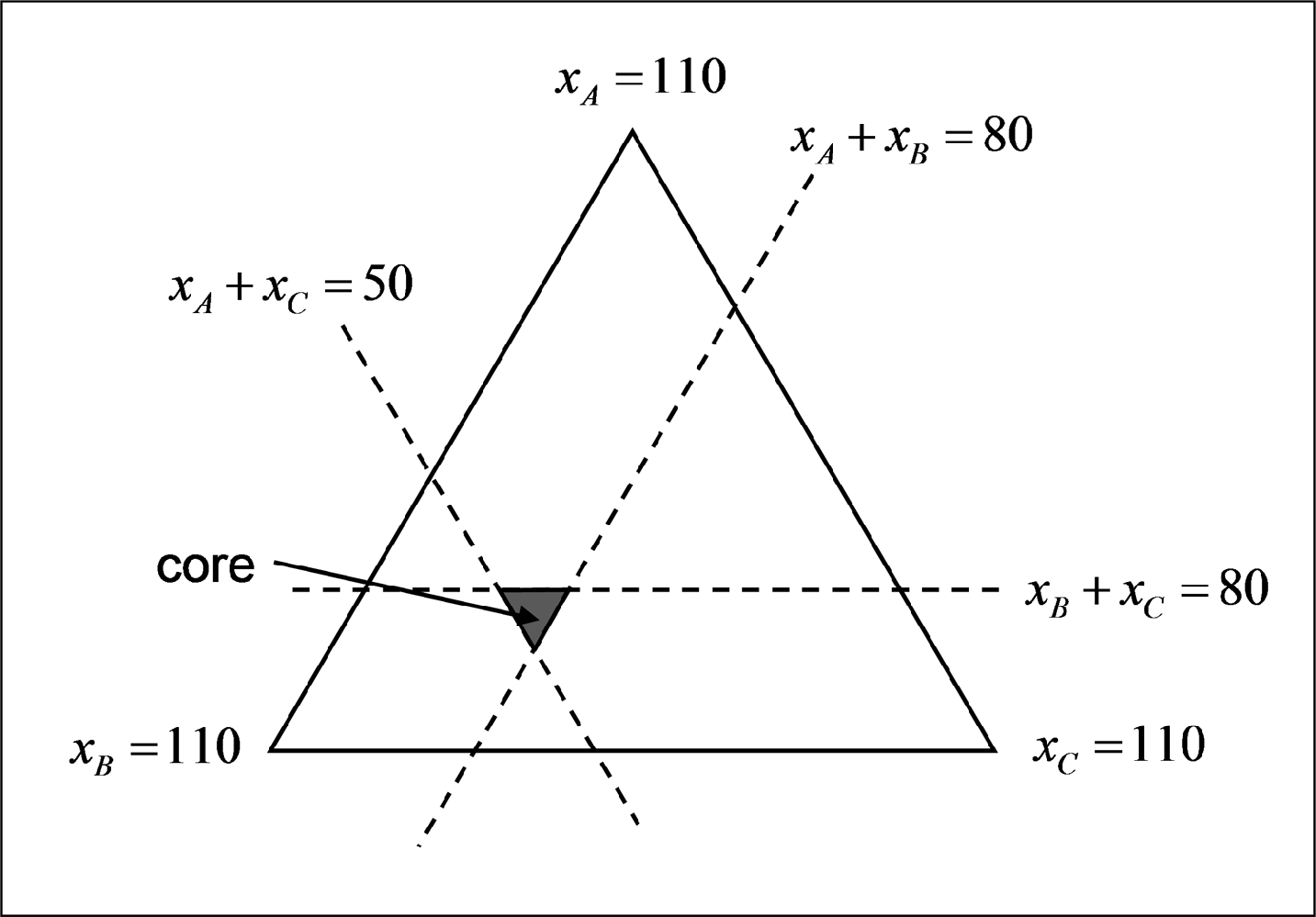
所有满足这些条件的分配集构成核心。该博弈的核心不是空的（参见图1）。

整个三角形构成了分配集。顶点是某家公司独占全部协同利润的点。这些位置无法执行，因为还可能存在两人联盟，从而使其他公司获得更高的收益。在满足所有这些约束条件后，核心即为所有不被支配的分配组成的集合。

仍然存在。图1显示，核心概念仅提供一组可能的解。为了得出具体的成本分摊方案，下一部分将考察夏普利值、核仁和τ‐值。

4.3 精确成本分摊的计算

夏普利值根据定义5计算得出。对于公司A和C，成本份额（单位：千欧元）结果为
$$
\phi_A(v) = \phi_C(v) = \frac{1}{3}(0) + \frac{1}{6}(80) + \frac{1}{6}(50) + \frac{1}{3}(30) = \frac{95}{3}.
$$
对于公司B，使用定义5计算的夏普利值结果（单位：千欧元）为
$$
\phi_B(v) = \frac{1}{3}(0) + \frac{1}{6}(80) + \frac{1}{6}(80) + \frac{1}{3}(60) = \frac{140}{3}.
$$
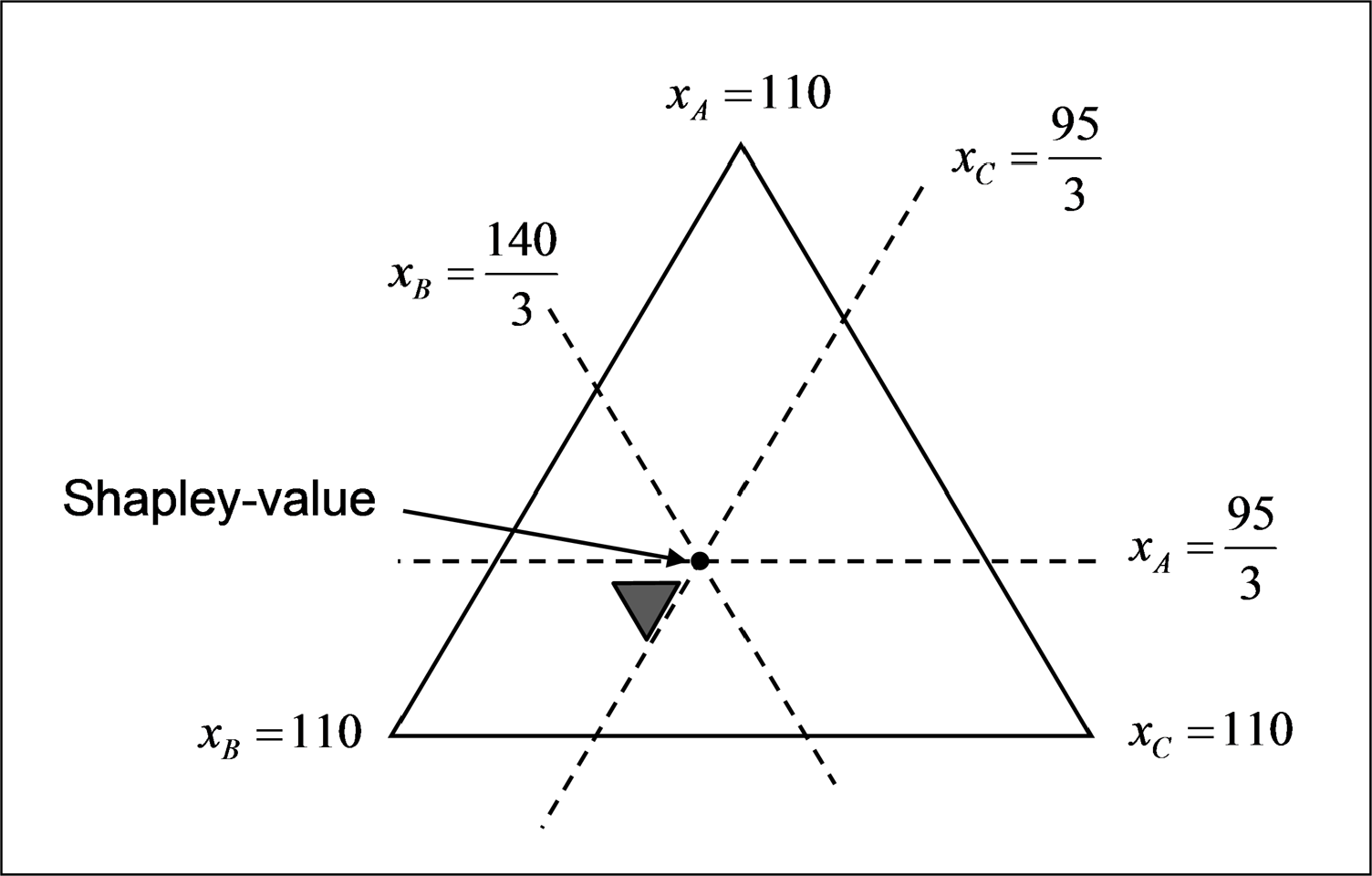
夏普利值的位置如图2所示。可以看出，该解不属于核心。这一结论也可以根据成本降低函数来解释（参见表3）。公司A和C组成的双公司联盟仅产生50,000欧元的成本降低。而根据夏普利值，它们共同获得63,333.33欧元，超过了它们组成双公司联盟所产生的收益。相比之下，任何包含公司B的双公司联盟所获得的分配都少于其应得份额。这意味着该解可被公司B阻止，因此不是稳定的。

核仁的计算基于定义6至9，这导致了以下结果：
$$
nuc_A = nuc_C = \frac{80}{3}, \quad nuc_B = \frac{170}{3}.
$$
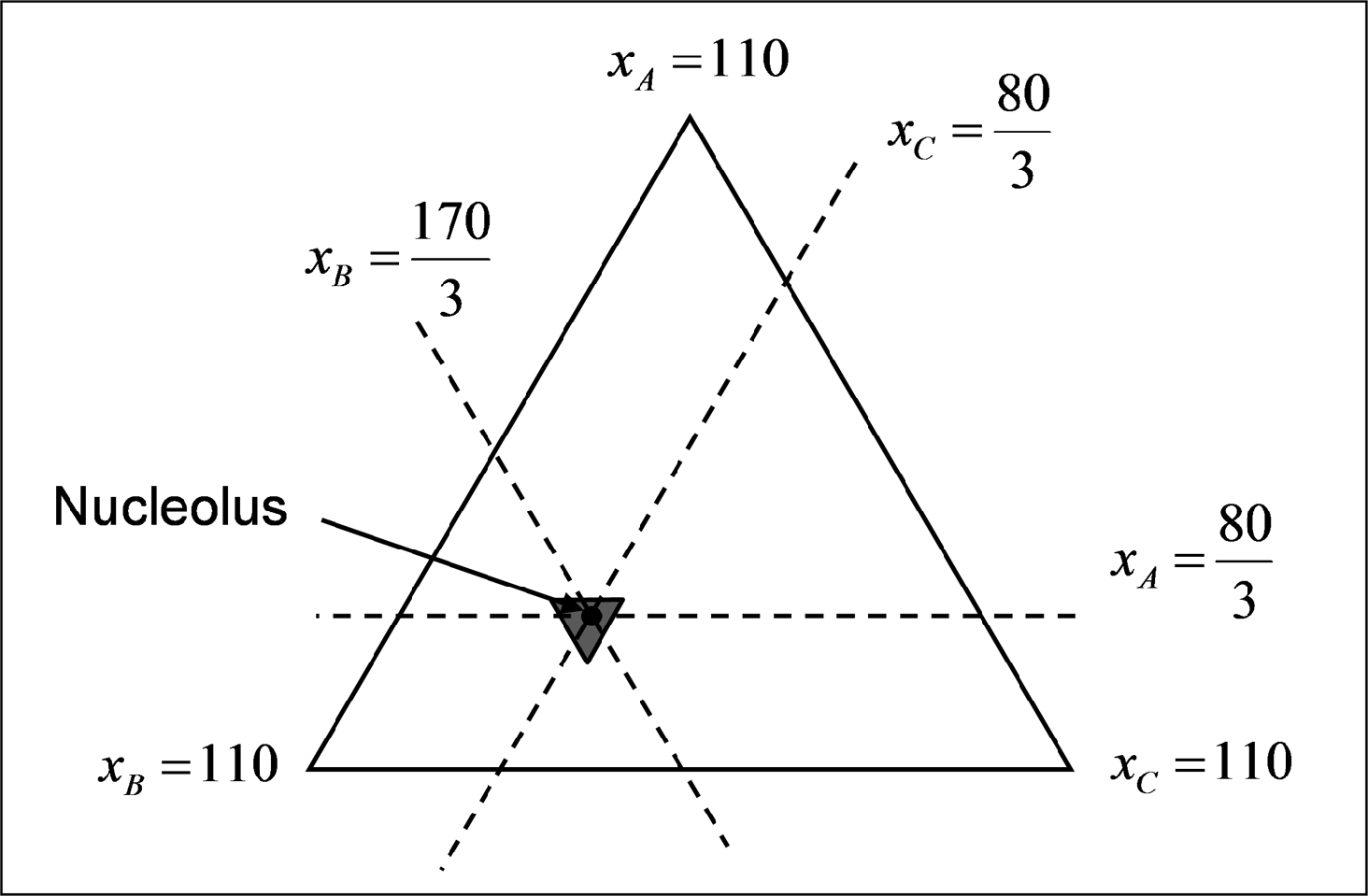
核仁的位置如图3所示。从中可以看出，核仁属于核心，因此可被归类为一个不受支配的稳定解。

下一步将计算τ的值。为此，需要计算上向量和下向量。上向量根据定义10得出
$$
b = \begin{pmatrix} b_A \ b_B \ b_C \end{pmatrix} = \begin{pmatrix} v(N) - v({B,C}) \ v(N) - v({A,C}) \ v(N) - v({A,B}) \end{pmatrix} = \begin{pmatrix} 30 \ 60 \ 30 \end{pmatrix}.
$$
下向量基于所有可能的外部联盟的最大值，并根据定义11生成，其中
$$
a = \begin{pmatrix} a_A \ a_B \ a_C \end{pmatrix} = \begin{pmatrix} \max(v({A}) - b_A, v({A,B}) - b_A - b_B, v({A,C}) - b_A - b_C, v({A,B,C}) - b_A - b_B - b_C) \ \max(v({B}) - b_B, v({A,B}) - b_A - b_B, v({B,C}) - b_B - b_C, v({A,B,C}) - b_A - b_B - b_C) \ \max(v({C}) - b_C, v({A,C}) - b_A - b_C, v({B,C}) - b_B - b_C, v({A,B,C}) - b_A - b_B - b_C) \end{pmatrix} = \begin{pmatrix} 20 \ 50 \ 20 \end{pmatrix}.
$$
利用这些结果，τ‐值根据定义12得出如下
$$
\tau = a + \lambda(b - a) = \begin{pmatrix} 20 \ 50 \ 20 \end{pmatrix} + \frac{2}{3} \left( \begin{pmatrix} 30 \ 60 \ 30 \end{pmatrix} - \begin{pmatrix} 20 \ 50 \ 20 \end{pmatrix} \right) = \begin{pmatrix} \frac{80}{3} \ \frac{170}{3} \ \frac{80}{3} \end{pmatrix}.
$$
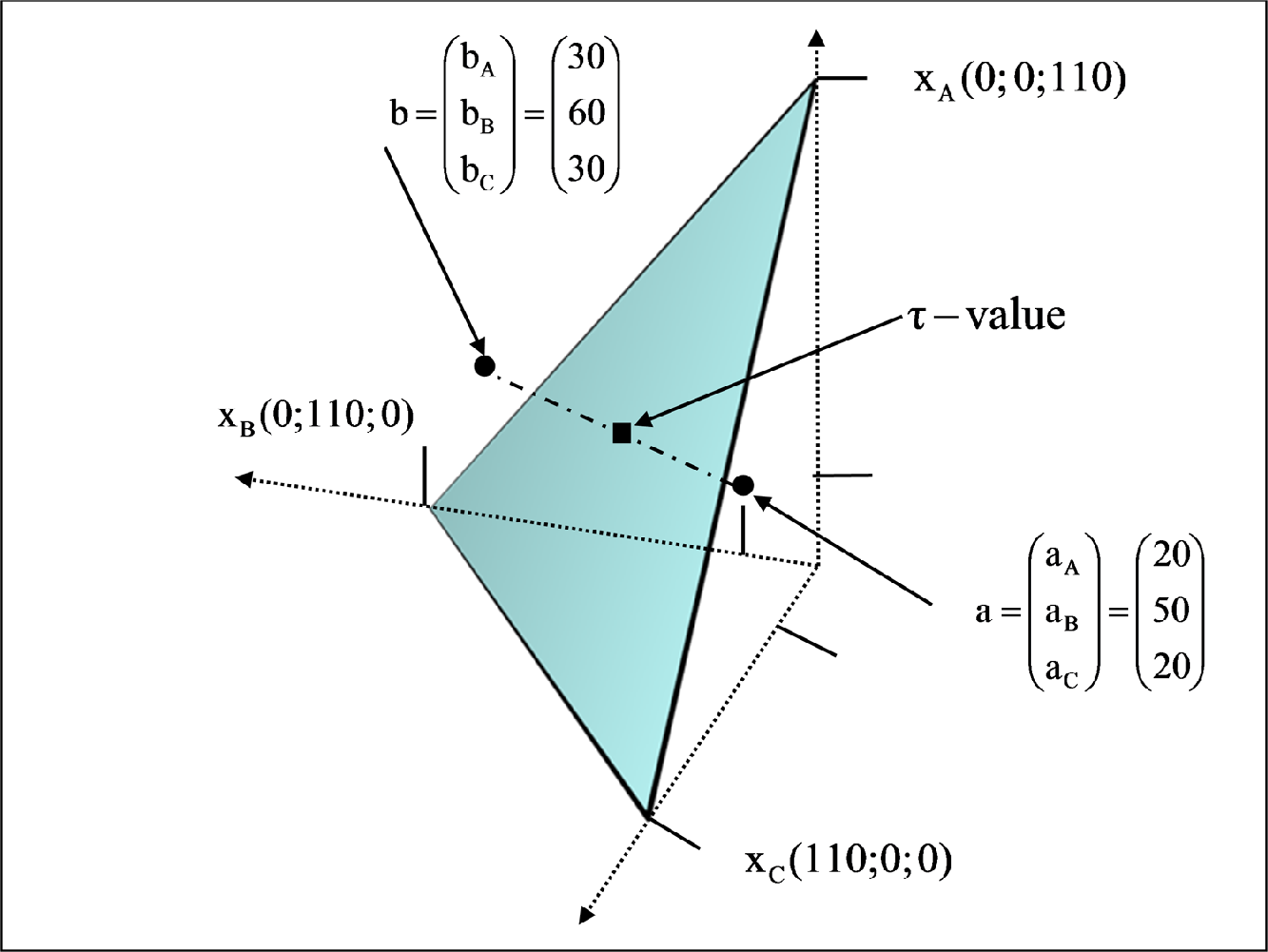
作为第一个结果，必须指出该例中的核仁与 τ‐值重合。为了更好地理解，将τ‐值的位置从图3中的二维三角形转换为空间图形（参见图4）。τ‐值的位置以及上限（乌托邦向量）和下限（核心向量）变得清晰可见。图4中的超平面由所有有效分配构成。

该示例表明，上限和下限不属于此平面，因为它们不是有效的。

以下将使用τ‐值/核仁生成的结果，因为夏普利值不在核心内。每家公司需承担的340,000欧元总成本份额，由独立解决方案与成本降低博弈中分摊份额之差决定。对于这三家公司而言，结果如下
$$
c_\tau(A) = c({A}) - v_\tau(A) = 150,000 € - 26,333.33 € = 123,333.33 €
$$
$$
c_\tau(B) = c({B}) - v_\tau(B) = 150,000 € - 56,666.67 € = 93,333.34 €
$$
$$
c_\tau(C) = c({C}) - v_\tau(C) = 150,000 € - 26,333.33 € = 123,333.33 €.
$$
这些结果即为各公司的成本分摊。对于公司A和C而言，该解提供了激励，因为在大联盟中的成本分摊从两人联盟{A, B}中的125,000欧元减少到了123,333.33欧元。对于公司B而言，基于τ值的解也提供了激励，因为其在大联盟中的成本分摊为93,333.33欧元，低于其独立方案的150,000欧元成本。

5 批评

5.1 一般性评论

必要的批评可以分为两部分：一部分涉及博弈论概念本身，另一部分则集中于所提出的分配方案。

博弈论解法概念面临的一个问题是，必须知道所有可能的联盟的合作收益。然而，通过合适的预测，可以避免这一问题，因此这对博弈论解法而言并非特殊难题。

另一个关键假设是合作伙伴之间存在侧向支付。上述分析的情况可以非常容易地解决这一问题，因为设备价格已知，并且必须由三位合作伙伴共同支付。这些支付即作为侧向支付。

合作博弈论中分配方案的推导表明，它们基于对个人与集体理性的要求。不同的解概念以特定方式规定了这些要求，从而实现利润的公平分配。通过满足公平性标准，确保了合作的稳定性。尽管对于相同的输入数据，不同的分配方案会得出不同的结果，这可能令人惊讶，但应结合各方案背后的不同理论依据来理解这一点。

5.2 解的概念详细评述

在总体批评合作博弈方法之后，还需进一步评述所讨论的各个解概念。为了比较不同的解概念，必须明确若干解概念应当满足的条件。首先，一个概念必须是有效的。解概念的有效性可分为理论效率和实际效率。实际效率由构建和使用模型的成本以及获取必要信息的成本决定。对于少量参与者的所有情况，博弈论概念均能满足该要求。随着参与者数量增加，计算将变得更加耗时。

计算夏普利值时，可能的联盟的排列数是关键因素。对于一组包含 N={1, 2, 3, …, n} 个参与者的集合，其排列数为 n!，因此由于超额向量的指数增长的分量数量，参与者数量较多时计算量会显著增加。

关于核仁的计算复杂度，必须提到的是，在参与者众多的博弈中，建立超额向量字典序的程序非常复杂。由于大联盟以及空联盟的超额值均为零，因此玩家集合 N={1,2,3…,n} 的超额向量包含 2^n − 2 个分量。这使得在大量参与者的情况下，核仁的计算变得更加复杂。

与这两种方法相比，τ‐值的计算更为简便。通常情况下，只能说明实际效率取决于问题、公司和/或具体情况。

理论效率概括了解的多种特征，涉及其一般要求以及特定的博弈论性质。理论效率的一般条件是
* 存在性
* 唯一性
* 解的可计算性。

可计算性是根据计算某个值的普遍可能性来判断的，而不考虑实际操作中的努力程度。

夏普利值始终存在，可计算，且始终是唯一的解。它是最常见的分配方案。τ‐值可以计算，其存在且仅对拟平衡博弈类有唯一定义，并且仅对该类博弈给出唯一解。核仁始终是唯一的，且可计算。

此外，必须证明已开发的特定博弈论性质，以确保结果的公平性。这些性质是
* 核心稳定性
* 个人与集体理性、虚拟参与者、对称性、可加性和单调性公理（第3.1节，第7‐9 页的公理1‐6）。

夏普利值仅在凸博弈中始终属于非空核心（Moulin，1988，第112–113页； Shapley，1971，第29页；Sudhölter 和 Peleg，1998，第386页）。如果博弈非凸，则夏普利值不一定属于核心。夏普利值是唯一满足个人与集体理性、虚拟参与者、对称性、可加性和单调性公理的单值解概念（马施勒等，2013年，第812页）。

对于τ‐值，无法保证它属于核心，即使在凸博弈中也是如此（Curiel，1997， 第13页；Driessen，1988，第130、131页；关于可使τ‐值成为核心一部分的凸博弈子类的讨论，参见Driessen 和 Tijs，1985；Muto 等，1989）。τ‐值是合理的，并满足虚拟参与者公理和对称性公理。但该值在总体上既不具有单调性（Tijs 和 Driessen，1986，第1022页），也不满足可加性要求（Tijs，1981，第6页）。

核仁始终是非空核心的一个成员，且是一种稳定解概念。如果核心非空，则核仁总是核心的一部分（Arin 和 Feltkamp，2005，第333页；Kruś 和 Bronisz， 2000，第264页；Schmeidler，1969，第1164页）。与夏普利值相比，核仁的主要优势在于，只要核心非空，它就始终属于核心（Schmeidler，1969，第1164页）。但早在1974年Megiddo就已证明，核仁在总体上不具备单调性，这似乎是其主要缺点（Young，1985，第68页）。此外，核仁不满足可加性公理，但满足上述其他公理（马施勒等，2013年，第812页）。

关于理论效率的上述研究成果总结于表4。

这些结果揭示了核心稳定性与单调性之间的权衡。核仁始终属于非空核心，但它不满足关键的单调性要求。夏普利值在总体上始终具有单调性，但对于所有类型的博弈而言，它并不总是属于核心。如果希望得到核心中的唯一结果，则必须面对一些不良的非单调性后果。但如果需要创造激励，那么单调性是本质的，此时核仁就不是一个应被推荐的解概念（马施勒，1992年，第614页）。

表4 理论效率条件及其被不同解概念的满足情况

概念	要求	夏普利值	核仁	τ-值
存在性与唯一性
唯一性	所有类型博弈均满足	所有博弈均满足	具有非空核心的拟平衡博弈
可计算性	可能	可能	可能
核心稳定性	满足凸博弈	满足所有博弈	具有非空核心	即使对于凸博弈也不满足
公理
• 个人与集体理性	满足	满足	满足
• 虚拟参与者	满足	满足	满足
• 对称性	满足	满足	满足
• 可加性	满足	不满足	不满足
• 单调性	满足	不满足	不满足

6 结论

合作是通过降低风险和成本来实现环境投资的一种有效方式。它有助于推动此类投资，并产生宝贵的积极生态效应。但合作也涉及合作伙伴之间的公平分配问题。就其经济效应而言，环境管理通常主张为合作伙伴创造一种双赢局面。这一主张的依据是一种规范性陈述，即产生了积极的生态效应，同时成本和风险得以降低。然而，这一假设只有在每个合作伙伴对共同成果作出相同贡献时才成立。而在企业实际所处的经济‐生态背景下，这一条件几乎从未得到满足。但绝大多数文献并未提出如何评估合作伙伴贡献不同的情形。为了实现积极的生态成果以及积极的经济成果，必须确保稳定的合作。这就要求合作伙伴之间对经济效益进行公平分配。“公平”的呼吁虽广受欢迎，但难点在于如何具体定义公平。为了确立对公平的普遍理解，本文从合作博弈论的视角分析环境管理背景下的合作企业。基于这一理论基础，提出了若干公理和条件，可作为检查清单。这些要求和公理使“公平”这一概念得以具体化。除了个体与集体理性、解的存在性等常见公理外，还引入了一些特殊公理。

核心稳定性与单调性是解决方案机制的关键性质，但二者彼此对立。由于研究结果具有较强的普遍性，这些公理及由此形成的检查清单处于一个高度抽象层次。为了指导寻找具体解的过程，来自合作博弈领域的不同解概念被用于合作博弈论被引入，并在一个案例研究中加以应用，同时结合所述公理进行了讨论。

结果表明，夏普利值和核仁在核心稳定性与单调性要求之间存在权衡。展示了这些模型适合作为决策引擎的情况。利用这些模型，可以评估环境投资项目中合作的公平性。这有助于实现双赢局面，而这正是此类合作的主要目标。

合作博弈论模型所基于的假设——特别是关于侧向支付以及有关未来发展的确切信息的假设——限制了其应用。这种博弈论视角并不能取代对公平分配的讨论，但它可以为这类讨论提供指导。

未来的研究可以聚焦于环境管理中成本分摊博弈的特征函数推导及其博弈性质的讨论。此外，在前述权衡背景下，评估夏普利值和核仁在环境管理问题中的适用性将是未来研究的挑战之一。需要明确决策者更偏好哪一种性质：核心稳定性还是单调性。