MR章节目录
第2章 配置空间 第3章 刚体运动 第4章 正向运动学 第5章 速度运动学与静力学 第6章 逆向运动学 第7章 闭链运动学 第8章 开链动力学 第9章 轨迹生成 9.1 定义 9.2 点到点轨迹 9.3 多项式通过点轨迹 9.4 时间最优时间缩放
第10章 运动规划 第11章 机器人控制 第12章 抓取与操作 第13章 轮式移动机器人
Modern Robotics, Chapter 9.4: Time-Optimal Time Scaling (Part 1 of 3)


在接下来的几个视频中,我们考虑以下
问题:
给定所需的路径 theta-of-s,
考虑机器人的动力学和
机器人关节处的扭矩限制,找到沿该路径的最佳时间缩放。
最短时间运动可用于最大限度地提高
机器人的生产率。
您可以想象尝试优化其他
标准,例如
执行器消耗的能量,但在接下来的几个视频中,
我们将重点关注时间最佳轨迹。
回想一下,机器人的动力学可以
写成 M 乘以 θ 双点加上
速度乘积项加上重力项,
等于关节力和扭矩矢量 tau。
在这里,我使用 Christoffel 符号矩阵 Gamma 编写了速度乘积项,
以强调它在关节速度矢量中是二次的
。
请记住,我们只
对机器人位于
路径 theta-of-s 上时的动力学感兴趣,我们可以将 theta-dot
和 theta-double-dot 重写为
路径相对于以下导数的函数 s
以及 s 对时间的导数。
将这些表达式代入动力学中,
我们得到此处所示的表达式。
由于路径是预先给定的,
theta 对 s 的导数也是预先已知的
,只有 s、s-dot 和 s-double-dot
是变量。
因此,我们可以将这个方程写为
向量方程 m-of-s 乘以 s-double-dot
加上 c-of-s 乘以 s-dot-squared 加上 g-of-s
等于 tau。
m-of-s、c-of-s 和 g-of-s 中的每一个都是
s 的向量函数,其中 c-of-s 乘以 s-dot-squared
是速度积项,g-of- s 是
引力项,m-of-s 起到质量的作用
。然而,
m 向量的某些元素可能为负
。
该方程是机器人
被限制沿路径
theta-of-s 移动时的动力学方程。
该方程没有说明
机器人偏离路径时的动力学。
现在我们已经用
单路径参数 s(而
不是关节矢量 theta)来表达动力学,我们必须考虑
机器人执行器可以产生的力或扭矩的限制。
第 i 个关节处的限制可以写
为 tau_i 大于 tau_i-min 且
小于 tau_i-max。
例如,tau_i-min 可以是负五
牛顿米,tau_i-max 可以是正五
牛顿米。
但一般来说,极限是
theta 和 theta-dot 的函数。
特别是,电动机可以产生的最大扭矩
通常
随着速度的增加而减小,直到
最终变为零。
请记住,
当机器人受限于路径时,我们可以用 s 和 s-dot 来表达 theta 和 theta-dot,
我们可以将
执行器限制重写为 s 和
s-dot 的函数。
如果我们将路径受限动力学的第 i 个分量替换
为 tau_i,我们
就会得到这些约束。
因此,
当机器人处于
(s,s-dot)状态时,第 i 个致动器对沿路径可能的加速度 s-double-dot进行了限制
为了确定第 i 个执行器对
s-double-dot 的限制,我们从所有三个表达式中减去 c_i 乘以 s-dot-squared
和 g_i,然后
除以 m_i。
由于 m_i 可以为正或负,因此
有两种可能的情况:如果 m_i 为正,
则 s-double-dot 的下限 L_i
和 s-double-dot 的上限 U_i
由以下等式给出 。
如果 m_i 为负,则 L_i 和 U_i
由这些方程给出。
这些方程告诉我们
沿着
关节 i 在状态 (s, s-dot) 下允许的路径的最大和最小加速度 s-double-dot。


如果我们计算所有关节的 L_i 和 U_i,
则 (s, s-dot) 的 L,
即状态 (s, s-dot) 下的最小可行加速度 s-double-dot
,就是下限中的最大值
遍及所有关节。
类似地,(s, s-dot) 的 U,即最大可行
加速度 s-double-dot,只是
所有关节上限的最小值。
现在,我们可以将
机器人沿路径的加速度约束简洁地表达
为 s-double-dot 大于 (s, s-dot) 的 L
且小于 (s, s-dot) 的 U。
在某些状态下,L 实际上可能
大于 U,在这种情况下,没有可行的
加速度使机器人保持在路径上。
换句话说,如果机器人发现自己
处于这种状态,它必须立即
离开路径;执行器的强度
不足以让机器人保持在路径上。
当机器人高速移动时,通常会发生这种情况
。
现在我们已经将执行器约束减少
到 s-double-dot 大于 L 且
小于 U,我们可以在数学上将
时间最优缩放问题表达如下:
给定路径 theta-of-s,初始状态
s 和 s-dot 为零,并且
s 为 1 且 s-dot 为零的最终状态,我们
希望找到一个单调递增的二次可微分
时间尺度,它 (a) 满足终端
条件并且 (b) 最小化总和 行程
时间资本 T 同时满足执行器
约束。
这个问题可以用很好的图形
解释来解释,我们将在下一个视频中看到Modern Robotics, Chapter 9.4: Time-Optimal Time Scaling (Part 2 of 3)
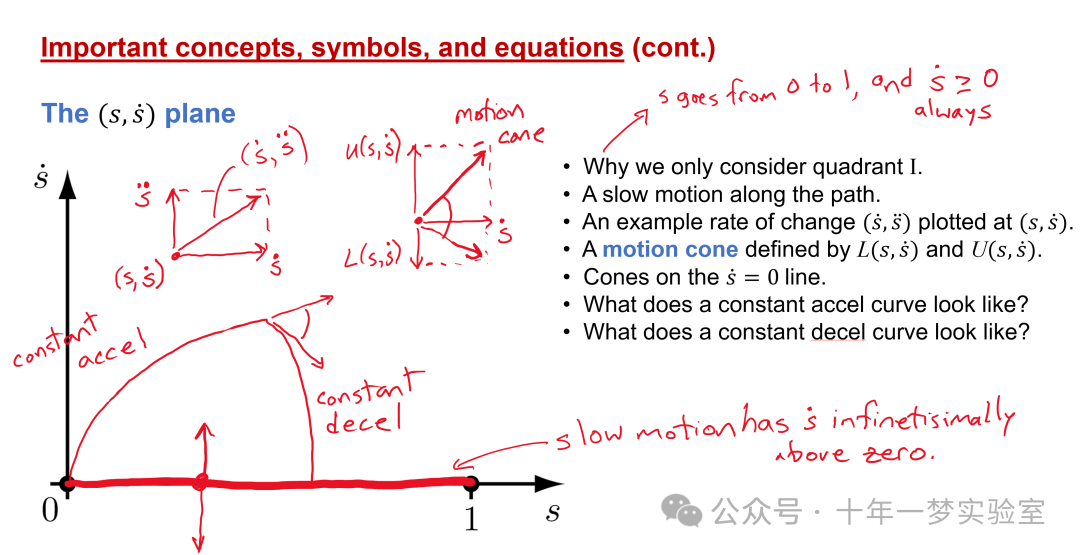
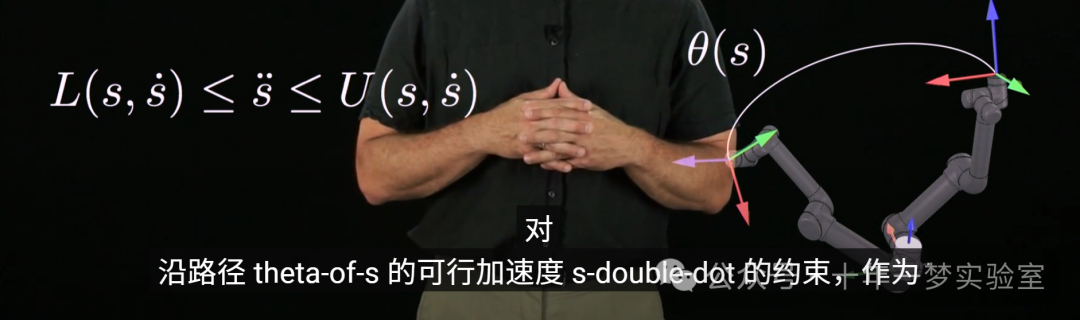
在上一个视频中,我们学会了将
机器人的关节力和扭矩限制表示为
对
沿路径 theta-of-s 的可行加速度 s-double-dot 的约束,作为
状态 (s, s-dot) 的函数。
在本视频中,我们将以图形方式表达这些约束,
并深入了解
时间最优的时间缩放问题。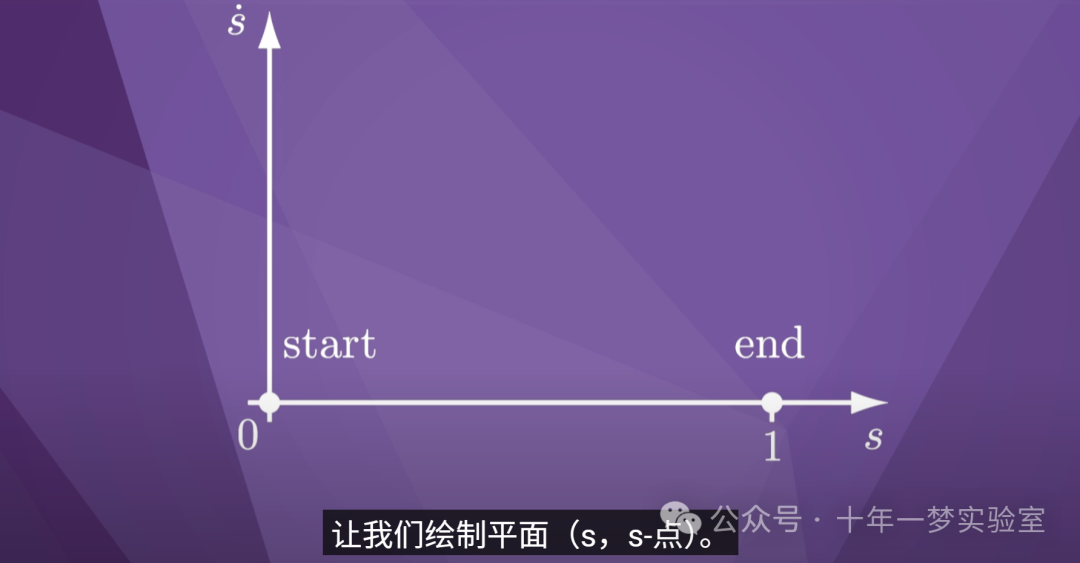
让我们绘制平面(s,s-点)。
运动开始时,s 和 s-dot
均为零。
运动结束时,s 等于 1,
s-dot 等于 0。
开始和结束状态显示为点。
由于我们要求沿着路径的运动
是单调的,即机器人总是
沿着路径向前移动,所以s-dot必须始终为
正。
所以我们只需要绘制
(s,s-dot)平面的右上象限。
如果机器人沿着路径移动非常缓慢,
那么机器人的运动
从开始到结束基本上都是沿着 s 轴的。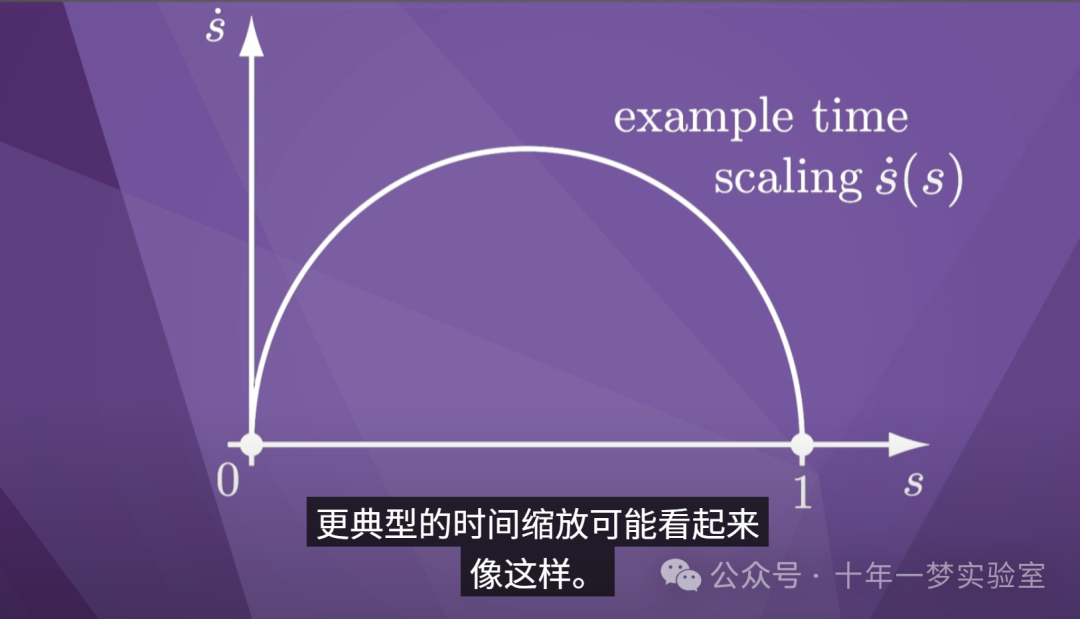
更典型的时间缩放可能看起来
像这样。
s-dot 从零开始,增加到
最大值,然后在运动结束时回落到零
。
到目前为止,我们一直将时间尺度表示
为 s 作为时间的函数,但在这里我们将
其绘制为 s 点作为 s 的函数。
相同的时间缩放可以用任何一种
方式表示,但在这个时间最优问题中,将
时间缩放表示
为 s-dot-of-s 更方便。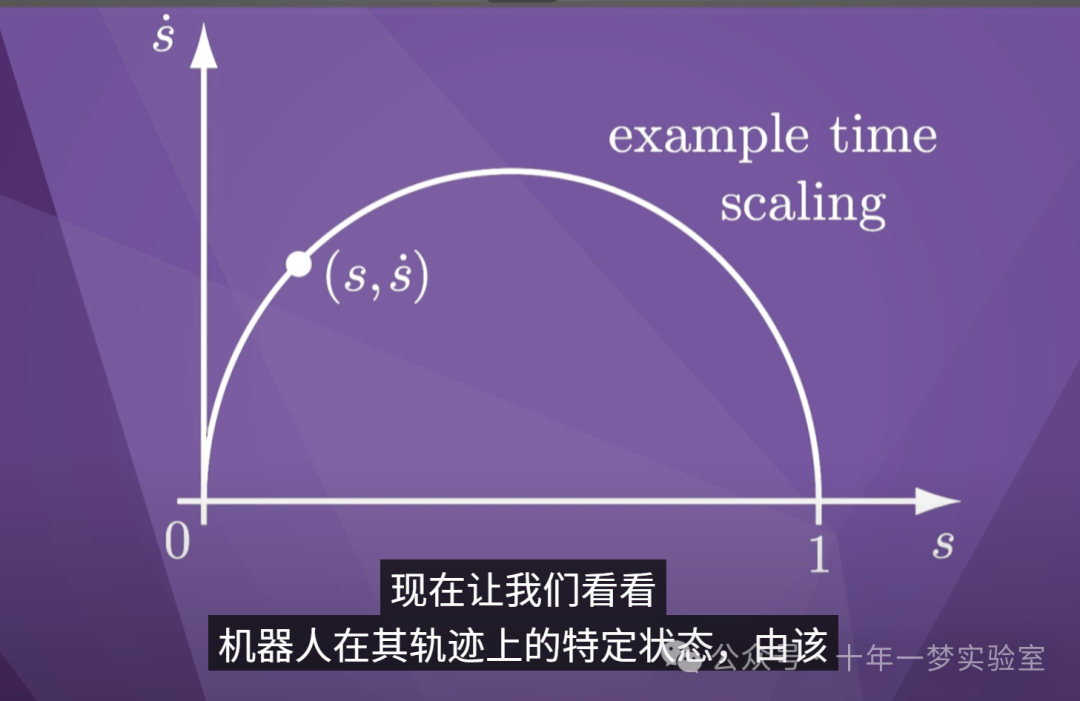
现在让我们看看
机器人在其轨迹上的特定状态,由该
点(s,s-点)表示。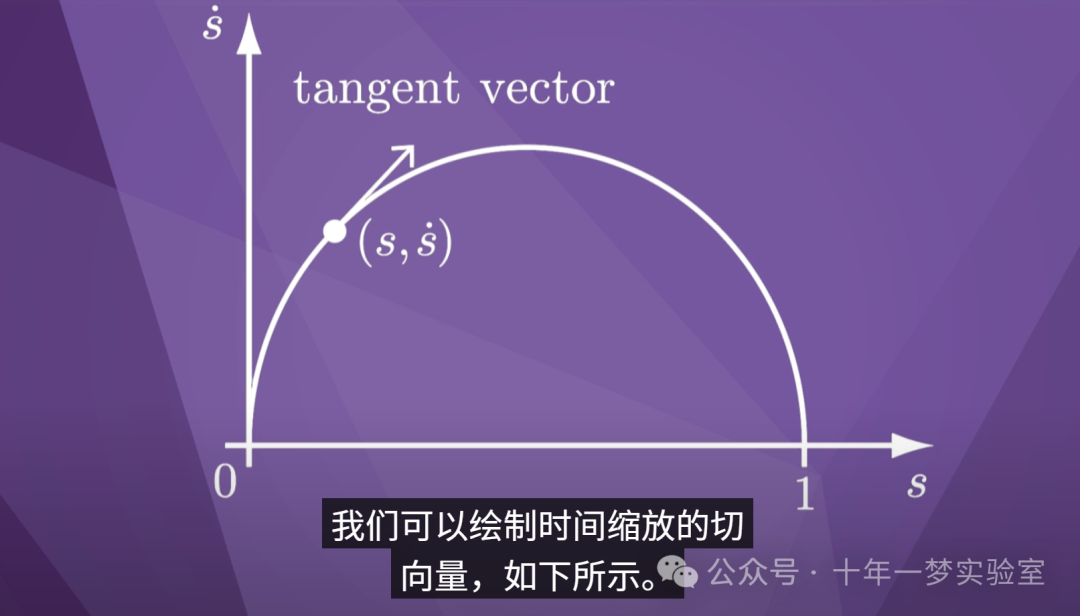
我们可以绘制时间缩放的切
向量,如下所示。
现在让我们摆脱时间缩放,这样我们
就可以专注于这个切向量。
切向量由水平
分量和垂直分量组成。
水平分量表示
s 的变化率,因此它就是 s-dot,
可以
沿 s-dot 轴绘制为与点的高度成正比。
垂直分量表示
s-dot的变化率,换言之,加速度
s-double-dot。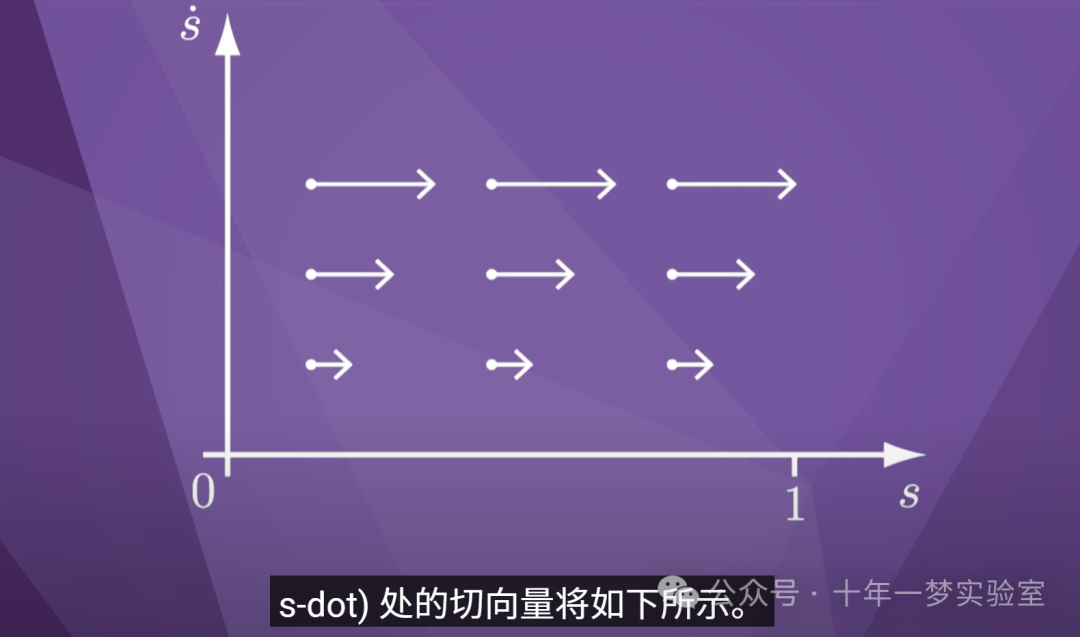
如果我们假设 s-double-dot 始终
为零,那么状态 (s,
s-dot) 处的切向量将如下所示。
矢量的水平分量
由点的 s 点值确定。
现在让我们关注
状态 (s, s-dot) 处的一个特定切向量。
水平分量是s点。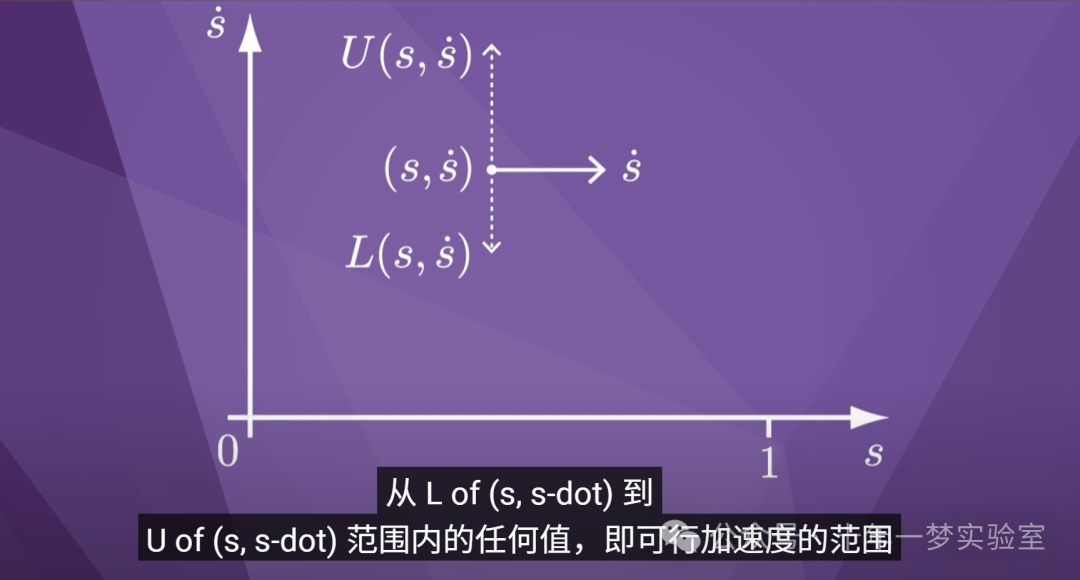
但现在我们假设垂直分量,即
加速度 s-double-dot,可以是
从 L of (s, s-dot) 到
U of (s, s-dot) 范围内的任何值,即可行加速度的范围
根据动态。
将这些垂直向量与水平
向量相加,我们得到此处显示的向量。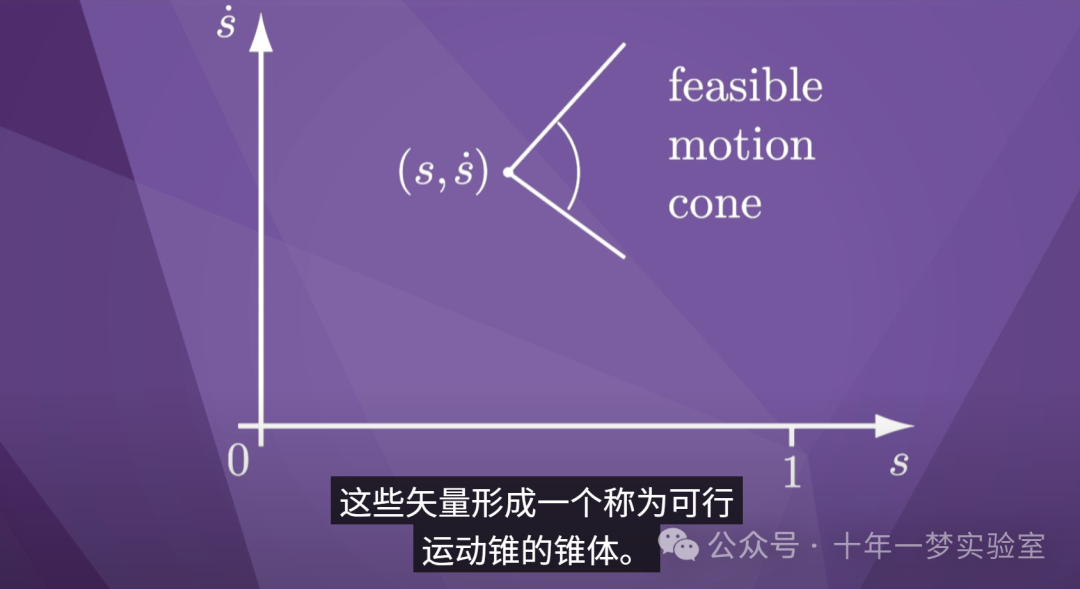
这些矢量形成一个称为可行
运动锥的锥体。
在此状态 (s, s-dot) 下,
时间缩放的切向量必须位于该锥体内
才能满足执行器限制。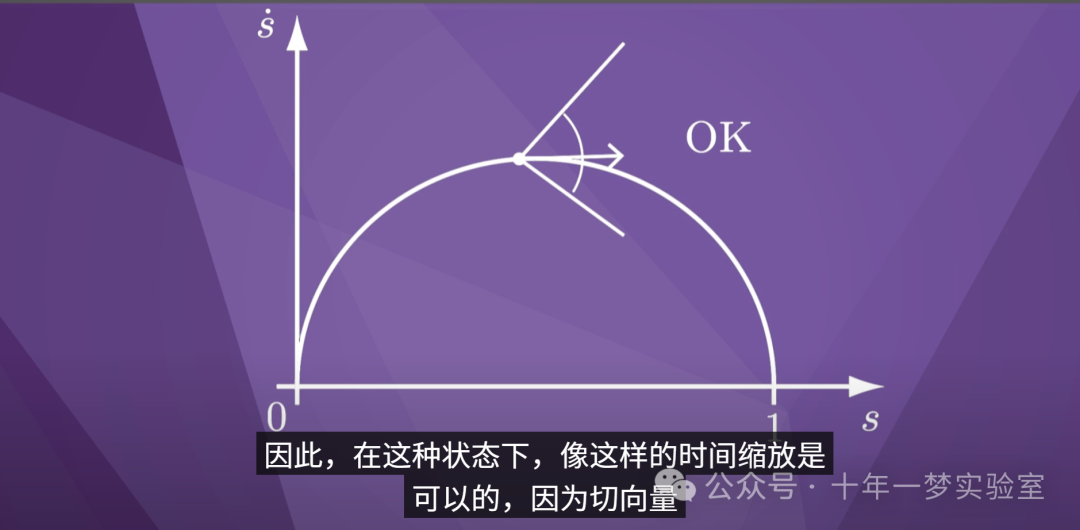
因此,在这种状态下,像这样的时间缩放是
可以的,因为切向量
位于可行的运动锥内。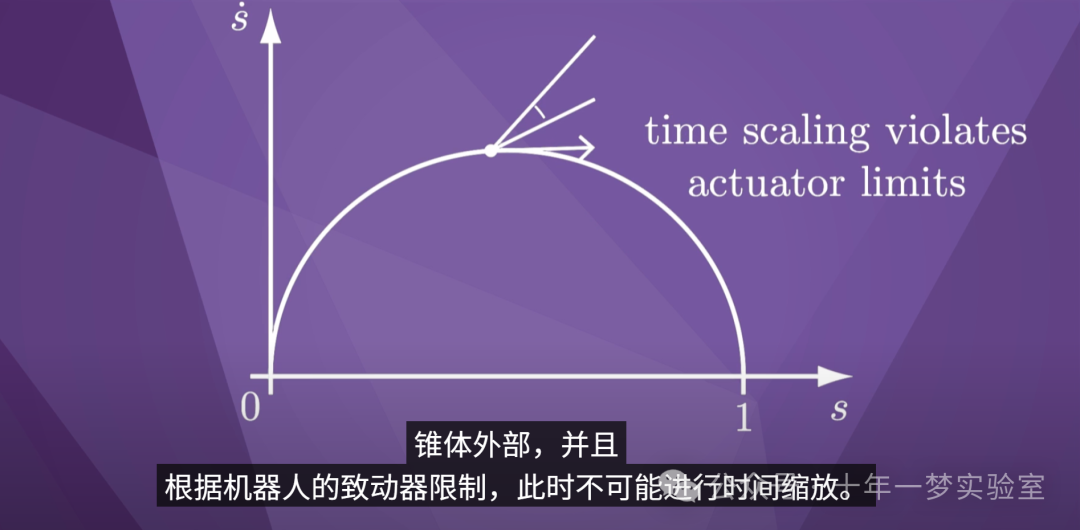
相反,如果我们的可行运动锥体
如下所示,则切向量位于
锥体外部,并且
根据机器人的致动器限制,此时不可能进行时间缩放。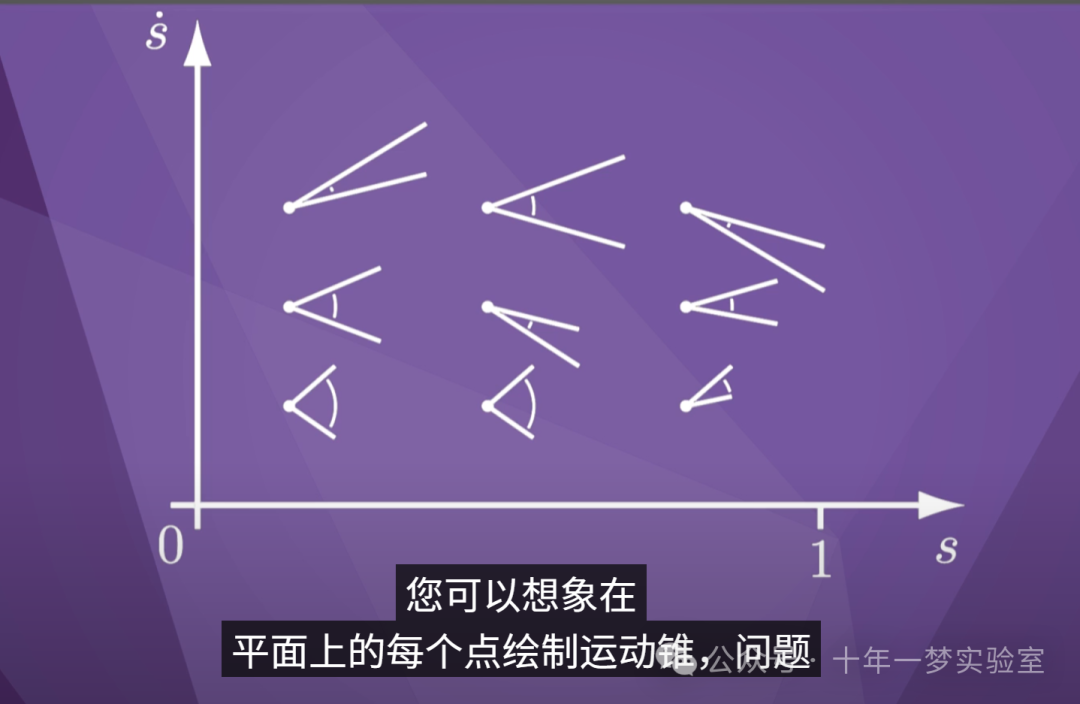
您可以想象在
平面上的每个点绘制运动锥,问题
是尽快从起始状态到达目标
状态,同时保持沿曲线的
所有运动锥内的时间缩放的切线
。
由于我们希望尽可能快,因此
时间缩放应始终尽可能高,
并且为了找到这样的时间缩放,我们可以从初始状态开始对
运动锥的上边缘进行前向积分
。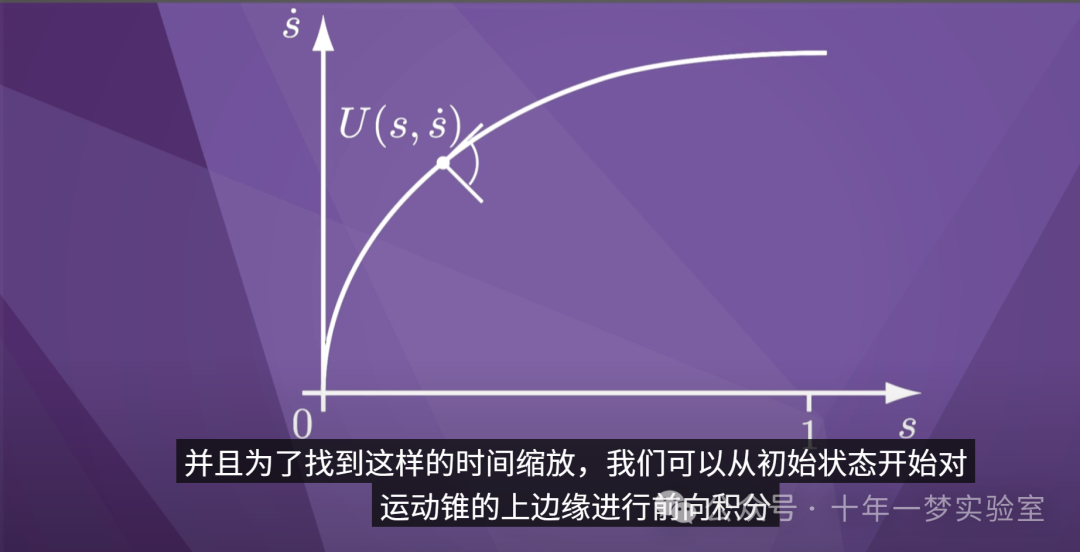
在这里,您可以看到一条通过对
最大可能加速度进行数值积分得出的曲线。
由于该曲线沿着
运动锥的边缘行进,因此至少有一个执行器
始终在极限状态下运行。
此时间缩放使机器人
尽可能快地沿着路径行驶,但不会根据需要
使机器人在路径末端停止
。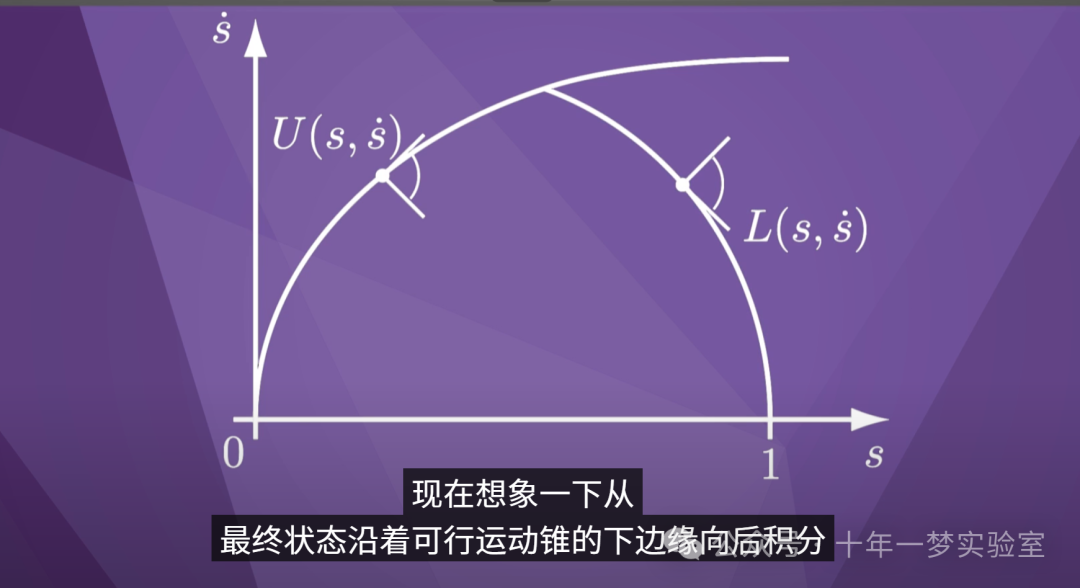
现在想象一下从
最终状态沿着可行运动锥的下边缘向后积分
。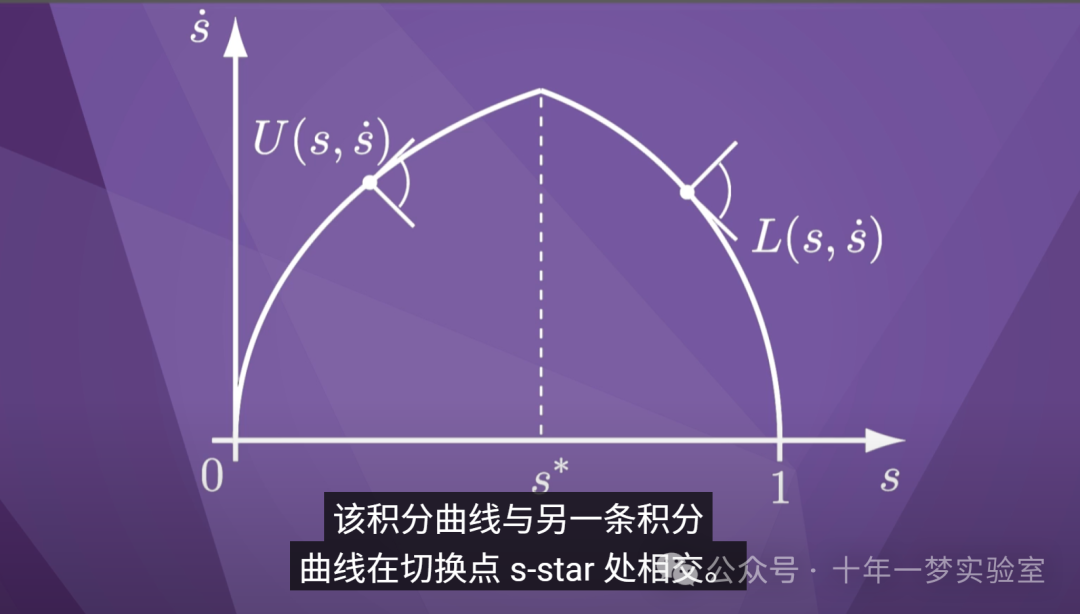
该积分曲线与另一条积分
曲线在切换点 s-star 处相交。
您在这里看到的时间缩放,
由数值积分获得的两段表示
,是时间最优的时间缩放。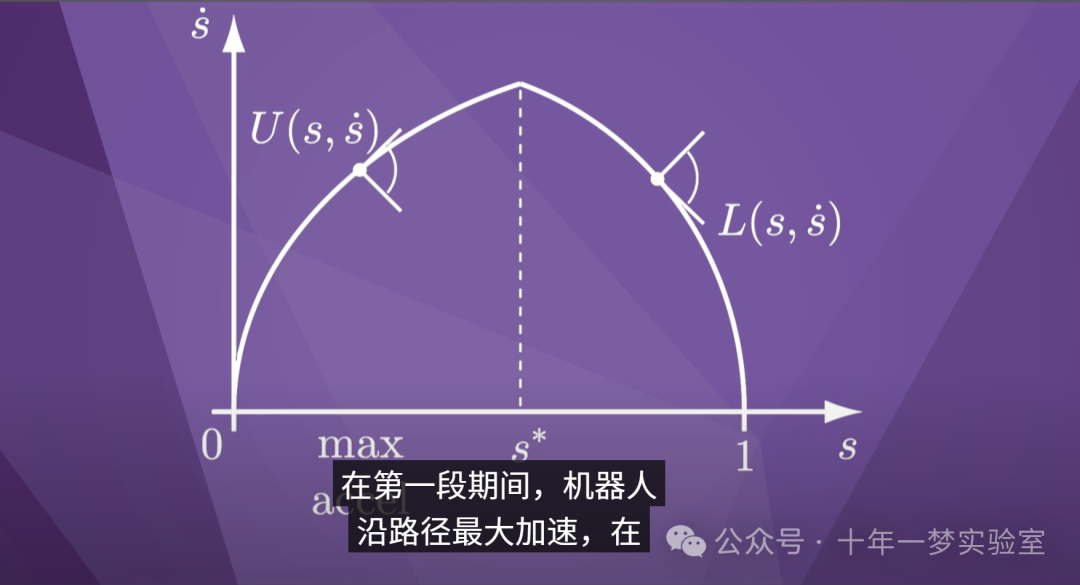
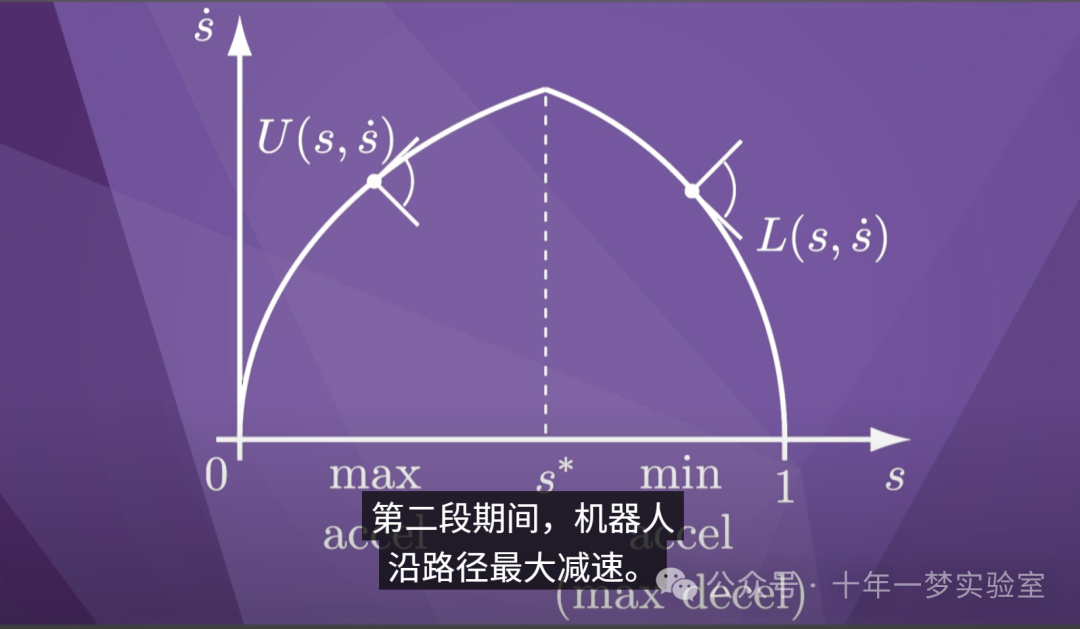
在第一段期间,机器人
沿路径最大加速,在
第二段期间,机器人
沿路径最大减速。
很明显为什么这是时间最优的:在第一段中
,机器人不能走得更快,
而在第二段中,如果速度 s-dot
在任何给定的 s 上更高,机器人
将无法达到 一个停留。
这种时间缩放使速度 s-dot
在任何时候都保持尽可能高,因此
运动的持续时间尽可能短
。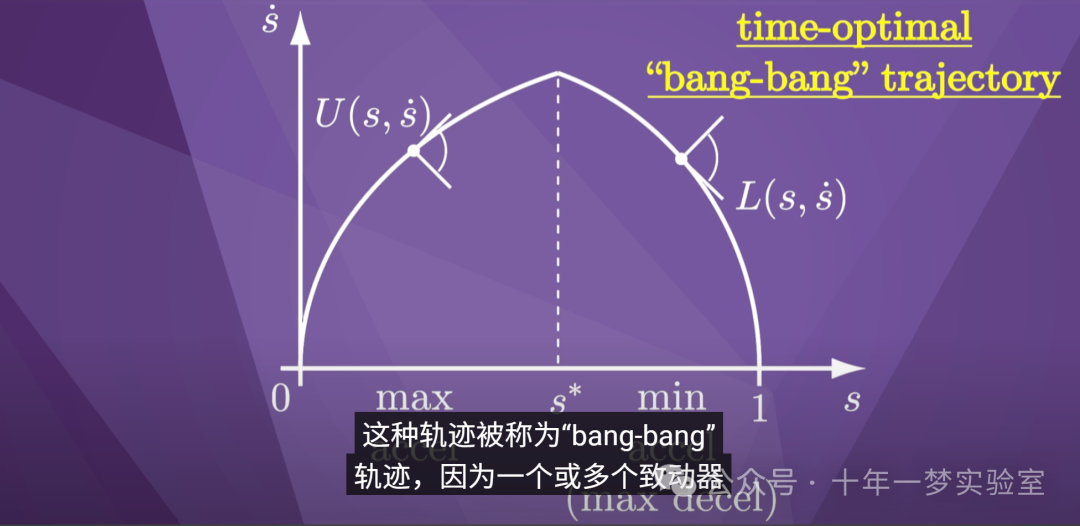
这种轨迹被称为“bang-bang”
轨迹,因为一个或多个致动器
在第一段期间“碰撞”限制,
然后一个或多个致动器
在第二段期间“碰撞”限制。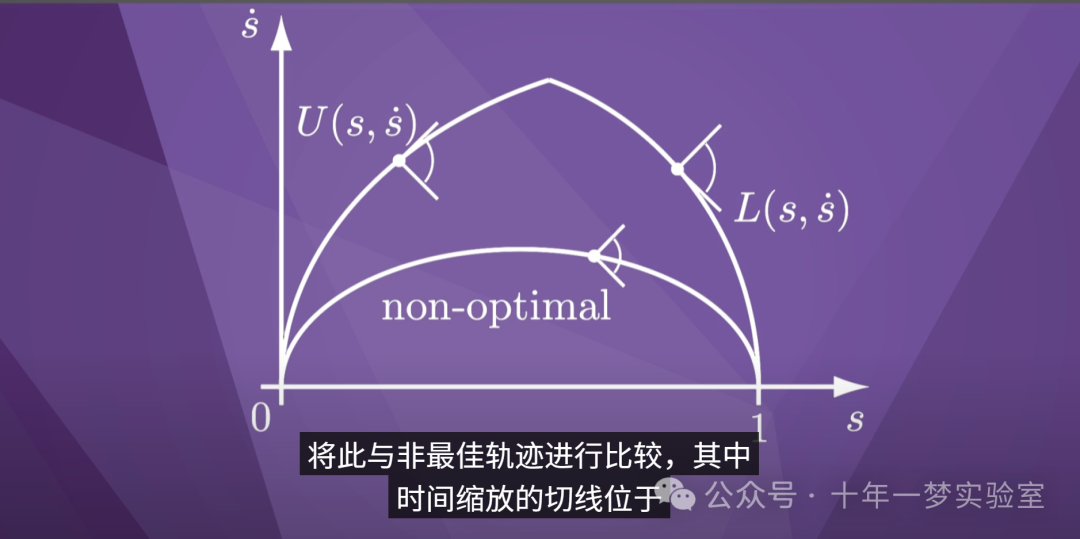
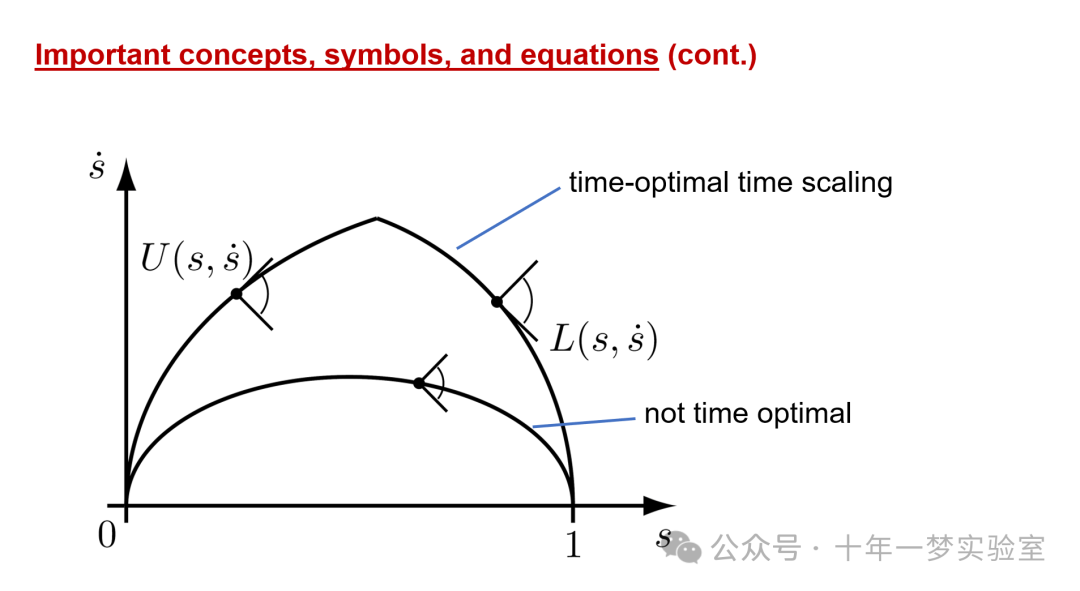
将此与非最佳轨迹进行比较,其中
时间缩放的切线位于
运动锥体的内部,而不是
边缘。
机器人在任何给定位置 s 的速度都
低于时间最优
时间缩放的速度。
这就是时间缩放算法背后的基本思想
,除了一个问题之外,我
现在将对此进行描述。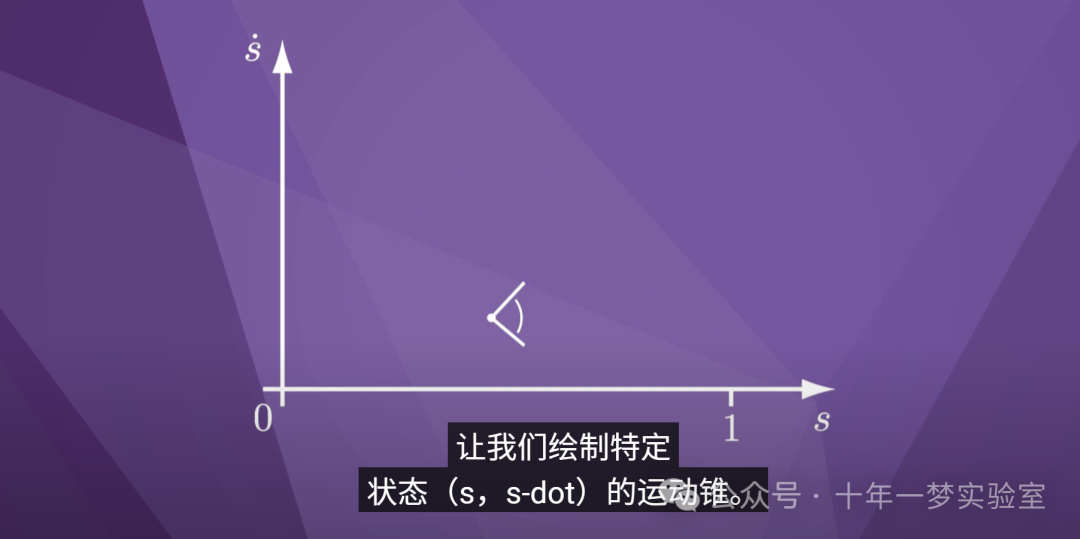
让我们绘制特定
状态(s,s-dot)的运动锥。
如果保持 s 不变但增加 s-dot,
您会得到不同的运动锥体。
如果进一步增加 s-dot,则运动
锥体可能会减小为单个矢量,其中
加速度下限与
加速度上限相同。
如果进一步增加 s-dot,则任何运动都是
不可行的,这意味着机器人的
行进速度太快,致动器无法将
机器人保持在路径上。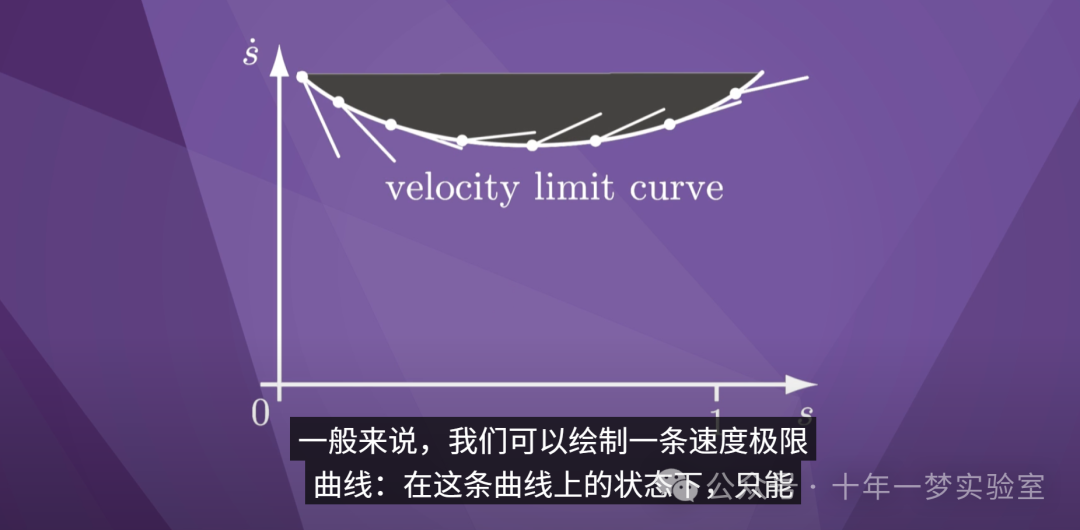
一般来说,我们可以绘制一条速度极限
曲线:在这条曲线上的状态下,只能
有一个加速度,在
这条曲线上方的状态下,机器人立即离开路径。
在曲线下方的状态,存在一个
可能的切向量圆锥。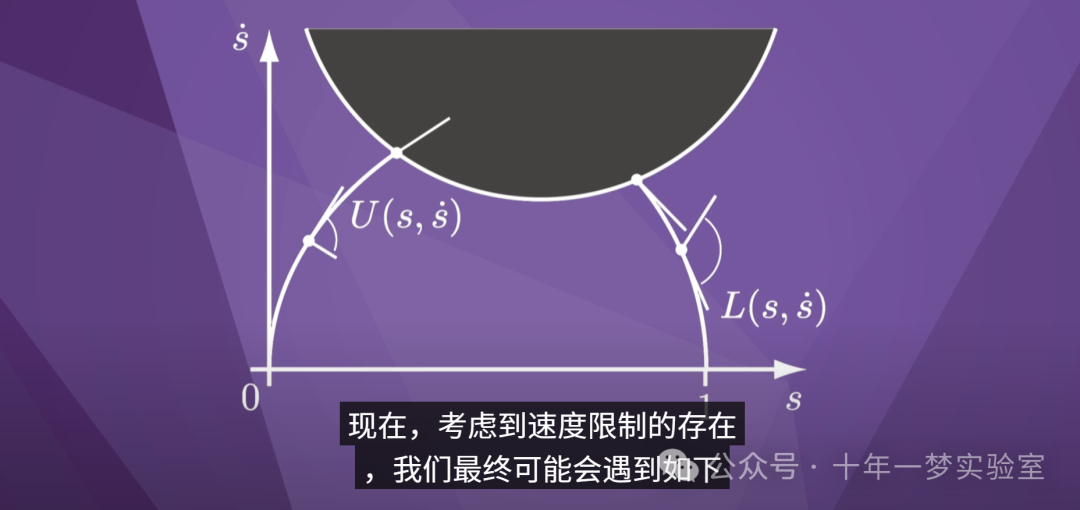
现在,考虑到速度限制的存在
,我们最终可能会遇到如下
所示的情况:最大加速度
曲线和最大减速度曲线
不相交,而是遇到
速度限制曲线。
因此,爆炸式控制是不可能的。
在这种情况下该怎么做是
第 9 章下一个也是最后一个视频的主题。Modern Robotics, Chapter 9.4: Time-Optimal Time Scaling (Part 3 of 3)

在之前的视频中,我们学习了
时间最优时间缩放问题的图形解释
。
基本上,我们尝试保持速度 s-dot
尽可能高,同时保持在
机器人执行器规定的运动锥内。
在某些情况下,时间最优解
由爆炸轨迹给出,其中
机器人最大加速然后最大
减速。
但在其他情况下,速度限制
曲线阻止了像这样的简单解决方案。
在第 9 章的最后一个视频中,我们开发了
一种算法来处理这种情况。
该算法的第一步是初始化,
您可以在书中找到。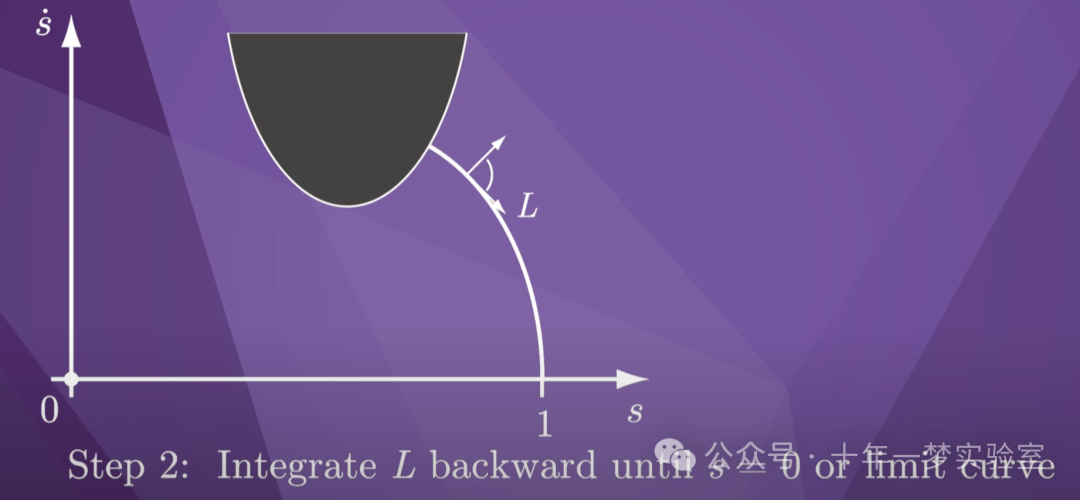
在步骤 2 中,我们
从最终状态向后积分最小加速度 L,直到
s 等于 0 或运动锥
在速度极限曲线处消失。
在这里所示的图中,我们到达了速度
极限曲线。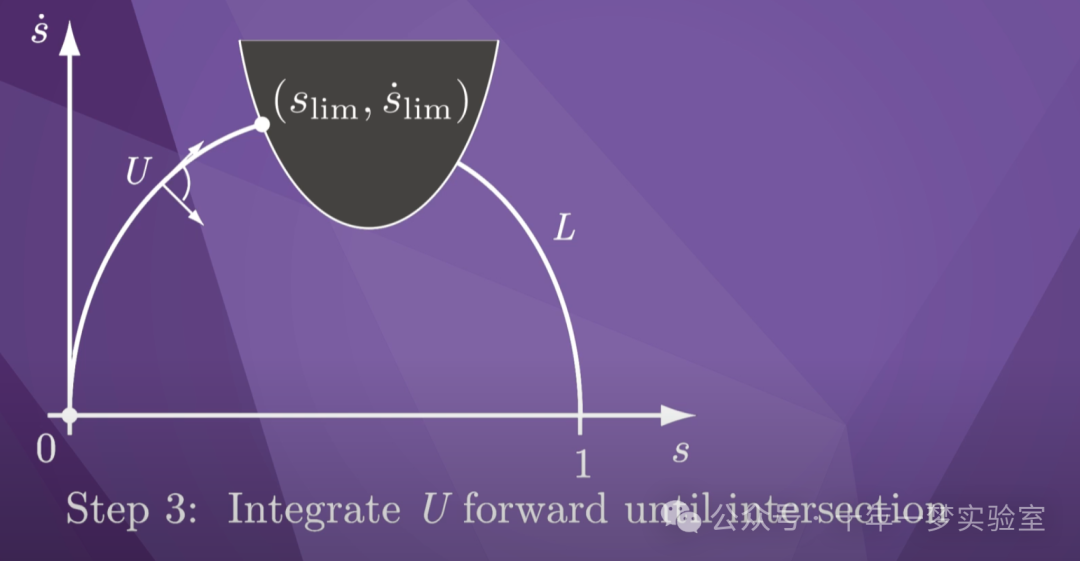
在步骤 3 中,我们对
从初始状态向前的最大加速度进行积分,直到与
最后一段或速度限制
曲线相交。
如果我们与最后一段相交,那么我们就
完成了:我们已经找到了最佳时间缩放。
在图中,我们
在(s_lim, s_lim-dot)处与速度限制曲线相交。
我们知道我们必须在
该交叉点之前的某个点减速,以避免
撞上速度限制曲线。
由于时间最优轨迹
仅由最大加速度 U 和最小加速度
L 组成,因此我们需要找到
从 U 切换到 L 的点。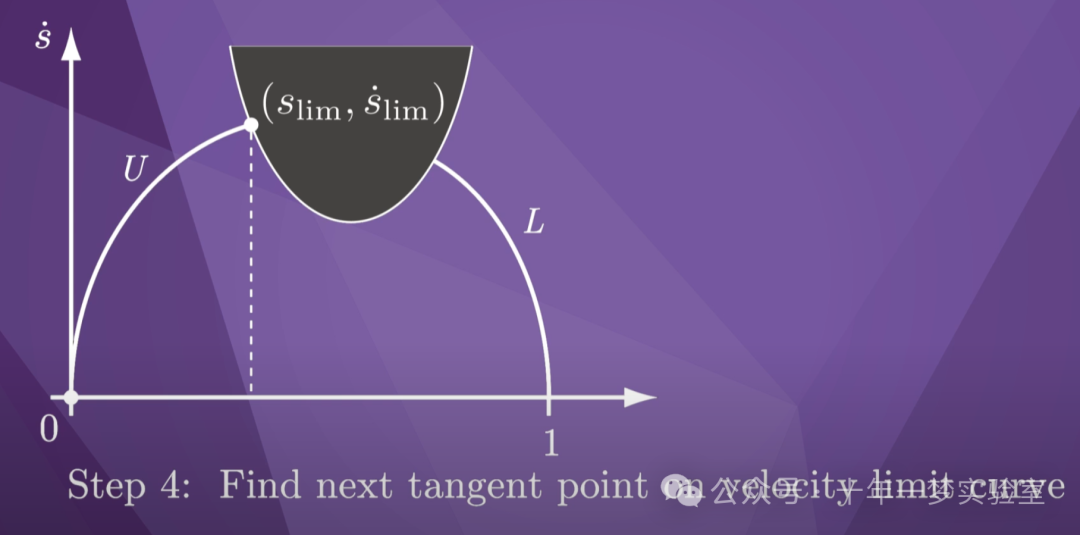
找到切换点的一种方法是
从我们所在的点降低速度 s-dot
达到速度极限曲线,并
向前积分最小加速度 L。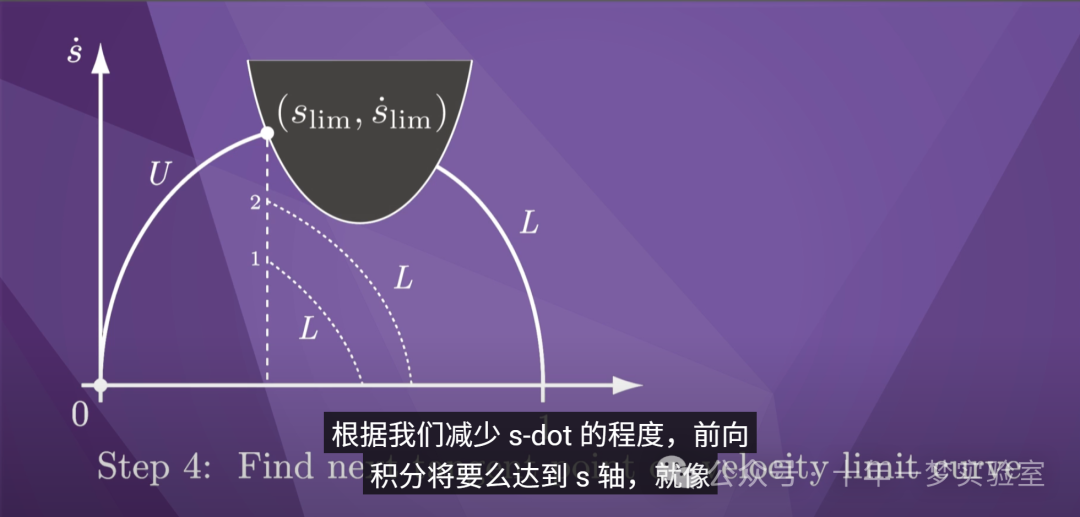
根据我们减少 s-dot 的程度,前向
积分将要么达到 s 轴,就像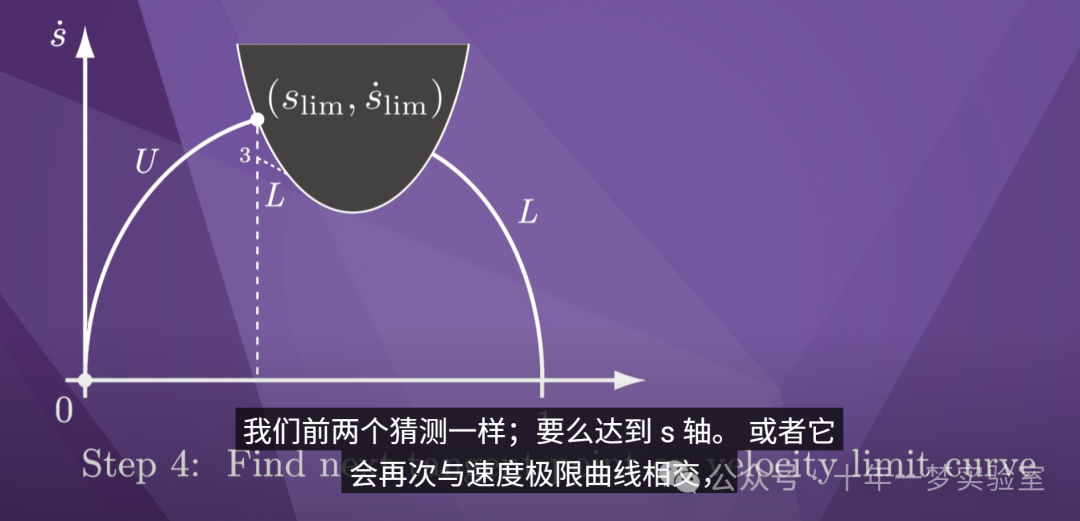
我们前两个猜测一样;要么达到 s 轴。 或者它
会再次与速度极限曲线相交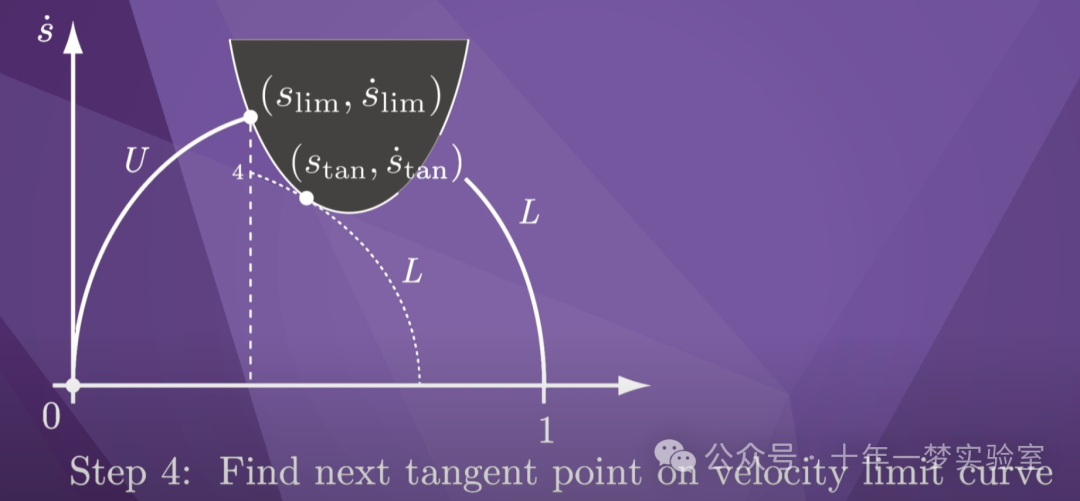
就像我们的第三个猜测一样; 否则它会切向接触
速度限制曲线。
我们正在寻找的正是这个切点
,我们将其称为 (s_tan, s_tan-dot)。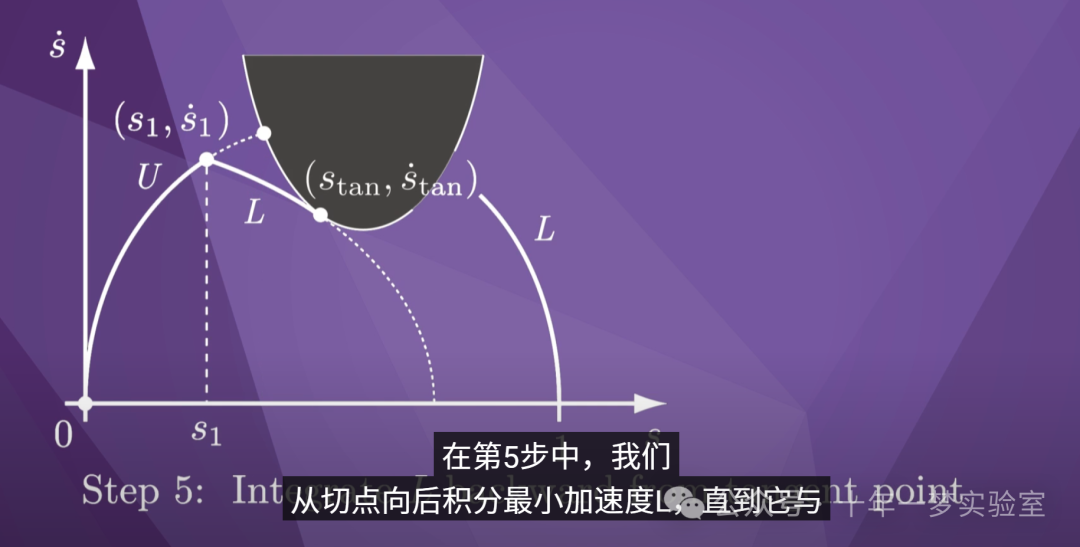
在第5步中,我们
从切点向后积分最小加速度L,直到它与
之前的U线段相交。
这是从最大
加速度到最小加速度的切换点s_1。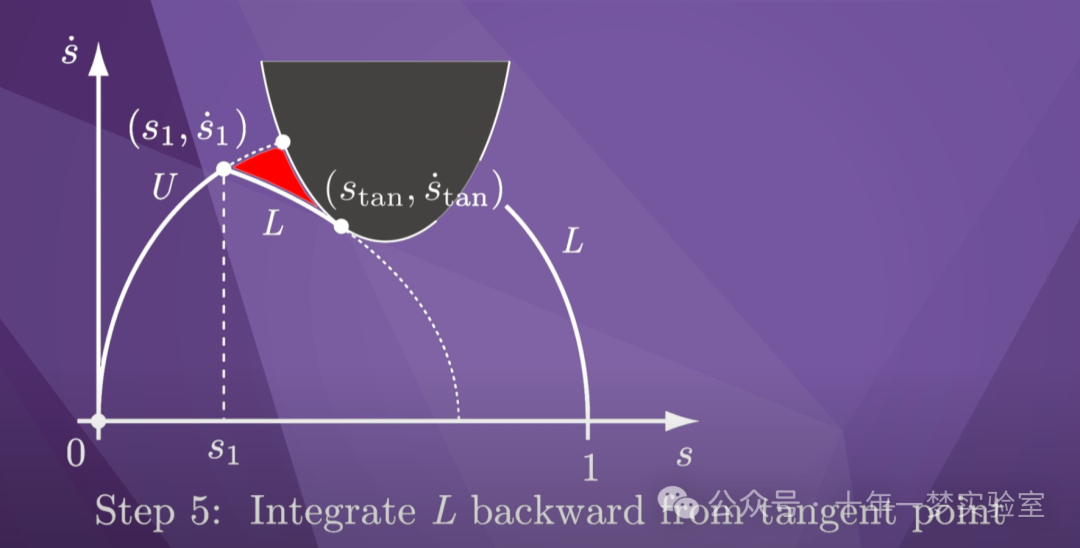
红色阴影区域中的状态最终将
与速度限制曲线发生碰撞,因此
必须避免它们。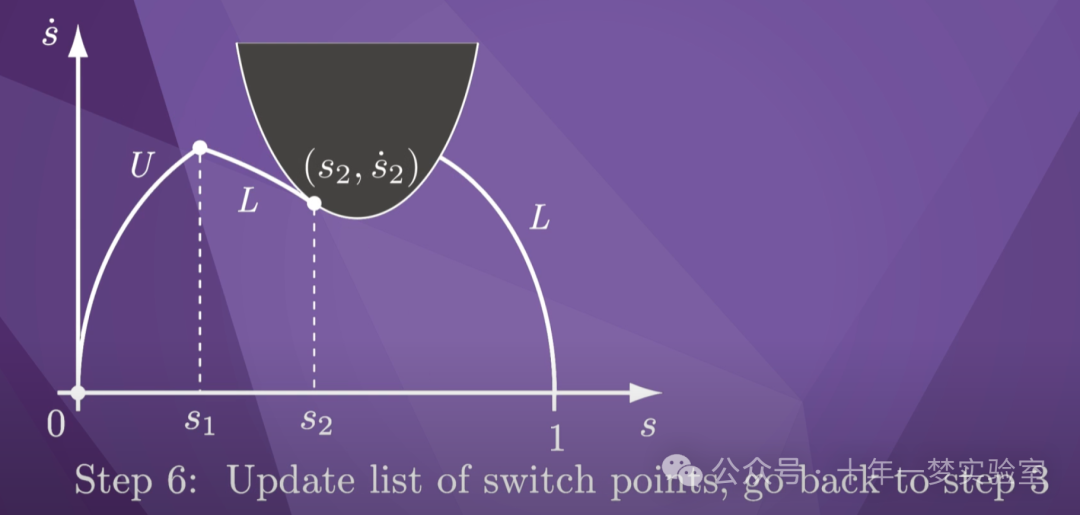
在步骤6中,我们将切点标记为
切换点s_2,在这里我们再次从
最小加速度L切换到最大加速度
U。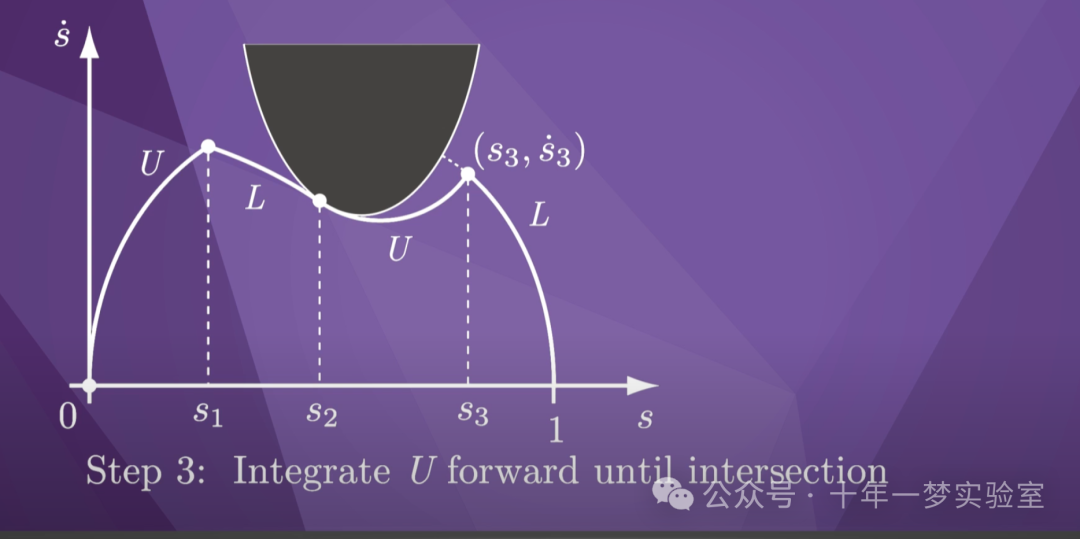
然后我们回到步骤3,
再次向前积分U。
该段将再次与速度限制
曲线相交,在这种情况下我们重复
刚才描述的过程,或者它将与
最后的 L 段相交,并且算法
完成。
如图所示,该算法
以三个切换点完成,时间最优
时间缩放由
直到 s_1 的最大加速度,然后是直到 s_2 的最小加速度
,然后是
直到 s_3 的最大加速度,然后是
使机器人达到 休息。
这种时间缩放使
路径上所有点的速度保持尽可能高,同时
确保轨迹对于执行器来说是可行的
。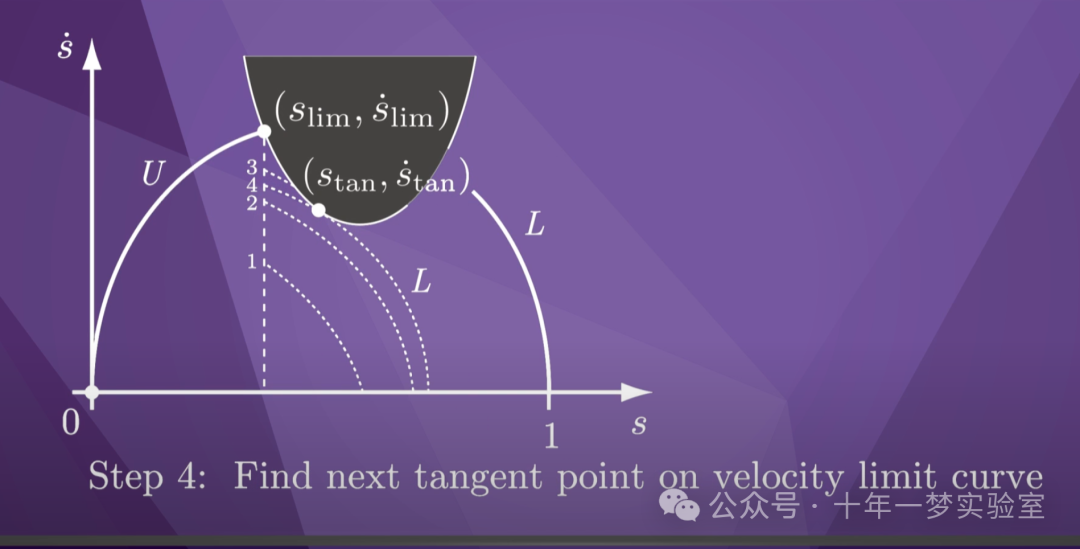
该算法的关键步骤是步骤 4,找到
速度极限曲线上的下一个切点
。 一种计算效率更高的方法
不是使用二分搜索猜测和检查
方法,而是以
数值方式构造
速度限制曲线并搜索
运动射线与曲线相切的下一个点。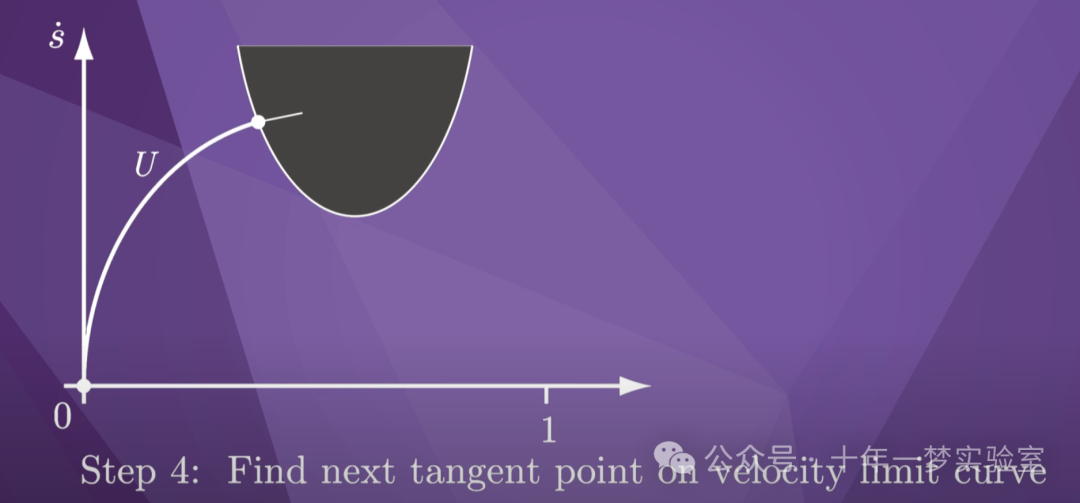
显然,在交点处,
运动射线进入不允许状态的区域
。
当我们沿着速度极限曲线搜索时,
我们最终找到曲线上
运动射线与极限曲线相切的点。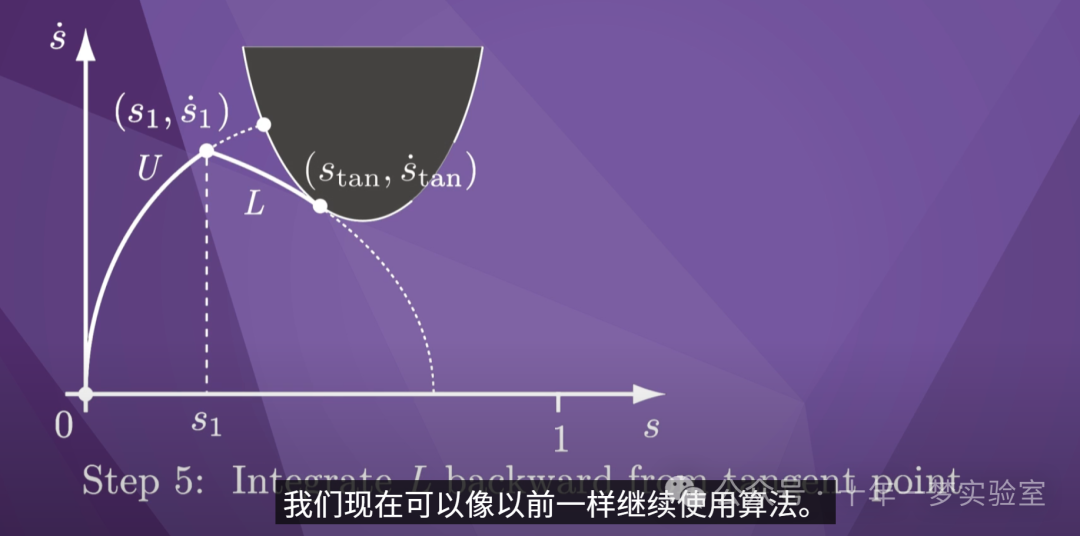
我们现在可以像以前一样继续使用算法。
还有一些其他的技术细节、特殊
情况和算法的改进,
其中一些在书中进行了描述,但
我给出的描述涵盖了最重要的点。
由于时间最优时间缩放要求
一个或多个执行器始终以最大
容量运行,并且由于动态
模型永远无法准确得知,因此该算法
很少直接用于轨迹生成。
尽管如此,它提供了对机器人
最大能力的深刻理论理解
。
第 9 章到此结束。
您现在了解了如何生成机器人轨迹的基础知识
,以及如何
使用第 8 章的动态方程来查找
沿指定路径的时间最优轨迹
。
在第10章中,我们将研究
障碍物之间的运动规划问题。



















 41
41

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








