三相永磁同步电机之五：电磁转矩

最新推荐文章于 2025-05-17 18:38:54 发布

原创最新推荐文章于 2025-05-17 18:38:54 发布 · 4.8k 阅读

35 ·

CC 4.0 BY-SA版权

文章标签：

#python

电机专栏收录该内容

3 篇文章

订阅专栏

电磁转矩是最重要的输出变量，决定着电机的机械动态特性。

1 磁场能量

1.1 磁能密度与磁共能密度

对于各向同性的导磁材质 $B=\mu H$ ，其磁能密度表示为：

$w_{m} = \frac{1}{2}BH=\frac{1}{2}\frac{B^{2}}{\mu }$

可以看出磁导率越大，磁场的储能密度就越小，对于磁导率很大的铁芯，其储存的磁能可以忽略不计，磁路的磁能几乎全部储存在气隙中。

由电磁感应定律得，线圈A产生的感应电动势为 $e_{AA}=-\frac{d\psi_{AA}}{dt}$ ，由基尔霍夫电压定律得：

$u_{A}=R_{A}i_{A}-e_{AA}=R_{A}i_{A}+\frac{d\psi_{AA}}{dt}$

在dt的时间内输入的净电能为（忽略漏磁）：

$dW_{eAA} = u_{A}i_{A}dt - R_{A}i_{A}^{2}dt=-e_{AA}i_{A}dt = i_{A}d\psi_{AA}=i_{A}d\psi_{mA}$

如果此时无机械运动的话，那么所有的净电能将全部转化为磁场能量的增量：

$dW_{m} = i_{A}d\psi_{mA}$

得到磁场能量的公式为：

$W_{m} =\int_{0}^{\psi_{mA}} i_{A}d\psi_{mA}$

以及磁共能公式（当磁路非线性时，磁场能量和磁功能不相等），大小示意图如下图所示：

$W_{m}^{'}=\int_{0}^{i_{A}}\psi_{mA}di$

磁能与磁共能之和为：

$W_{m}+W_{m}^{'}=i_{A}\psi_{mA}$

若假设铁芯的磁导率为无穷大，则磁场能量全部储存在气隙中：

$W_{m} = W_{m}^{'}=\frac{1}{2}i_{A}\psi_{mA}=\frac{1}{2}L_{mA}i_{A}^{2}=\frac{1}{2}f_{A}/N\cdot NB_{\delta }S = \frac{1}{2}f_{A}B_{\delta }S$

若存在双线圈A、B互感的情况：

$W_{m} = W_{m}^{'}=\frac{1}{2}i_{A}\psi_{A}+\frac{1}{2}i_{B}\psi_{B}$

$W_{m} = W_{m}^{'}=\frac{1}{2}L_{A}i_{A}^{2}+L_{AB}i_{A}i_{B}+\frac{1}{2}L_{B}i_{B}^{2}$

2 机电能量转换

要将磁场能量释放出来转换为机械能，前提是需要有可运动的部件。由于A、B线圈间的互感为转子位置角 $\theta_{r}$ 的函数对于互感的基波可以表示为( $M_{AB}$ 为互感的最大值)：

$L_{AB}(\theta_{r})=L_{BA}(\theta_{r}) = M_{AB}cos\theta_{r}$

此时，磁能和磁共能不仅是磁链的函数（因为电流与磁链关于电感耦合了，所以只需要取其中一个作为变量），还是转角 $\theta_{r}$ 的函数（电感中又混入了转角变量，所以需要再增加一个独立的变量）：

$dW_{m} = \frac{\partial W_{m}}{\partial \psi_{A}}d\psi_{A} + \frac{\partial W_{m}}{\partial \psi_{B}}d\psi_{B}+\frac{\partial W_{m}}{\partial \theta_{r}}d\theta_{r}$

$dW_{m} = i_{A}d\psi_{A} + i_{B}d\psi_{B}+\frac{\partial W_{m}}{\partial \theta_{r}}d\theta_{r}$

$dW_{m}^{'} = \psi_{A}di_{A} + \psi_{B}di_{B}+\frac{\partial W_{m}^{'}}{\partial \theta_{r}}d\theta_{r}$

可以看出转子的运动引起了气隙储能的变化，在磁场储能变化的过程中，将会又部分磁场能量转化为机械能。

电磁转矩为克服机械转矩所做的机械功：

$dW_{mech} = t_{e}d\theta_{r}$

根据能量守恒，机电系统的能量关系为（dt时间内输入系统的净电能=磁场吸收的总磁能+转变为机械能的总能量，忽略了损耗）：

$dW_{e} = dW_{m}+dW_{mech} = dW_{m} + t_{e}d\theta_{r}$

根据上式可得：

$t_{e}d\theta_{r} = dW_{e} - dW_{m}=-\frac{\partial W_{m}}{\partial \theta_{r}}d\theta_{r}$

$t_{e} = -\frac{\partial W_{m}(\psi _{A},\psi _{B,\theta _{r}})}{\partial \theta _{r}}$

$t_{e} = \frac{\partial W_{m}^{'}(\psi _{A},\psi _{B,\theta _{r}})}{\partial \theta _{r}}$

可以看出，电磁转矩的方向为在恒磁链下使得系统磁能减小的方向。上述公式对于线性和非线性磁路均适用，具有普适性。

将该式带入 $W_{m} = W_{m}^{'}=\frac{1}{2}L_{A}i_{A}^{2}+L_{AB}i_{A}i_{B}+\frac{1}{2}L_{B}i_{B}^{2}$ 得（此时假定正方向为逆时针）：

$t_{e}=i_{A}i_{B}\frac{\partial L_{AB}(\theta _{r})}{\partial \theta _{r}}=-i_{A}i_{B}M_{AB}sin\theta _{r}$

最大值出现在 $\theta _r=90^{\circ}$ 电角度的位置上。

气隙磁场作为电能与机械能相互转换的媒介，成为了两者的耦合场。

当转子旋转时，A、B绕组的感应电动势为：

$e_{A} = -\frac{\mathrm{d} \psi _{A}}{\mathrm{d} t} = -\frac{\mathrm{d} }{\mathrm{d} x}[L_{A}i_{A}+L_{AB}(\theta _{r})i_{B}] \newline =-[L_{A}\frac{\mathrm{d} i_{A}}{\mathrm{d} t} + L_{AB}(\theta _{r})\frac{\mathrm{d} i_{B}}{\mathrm{d} t}+i_{B}\frac{\partial L_{AB}(\theta _{r})}{\partial \theta _{r}}\frac{\mathrm{d} \theta _{r}}{\mathrm{d} t}]$

$e_{B} = -\frac{\mathrm{d} \psi _{B}}{\mathrm{d} t} = -\frac{\mathrm{d} }{\mathrm{d} x}[L_{B}i_{B}+L_{BA}(\theta _{r})i_{A}] \newline =-[L_{B}\frac{\mathrm{d} i_{B}}{\mathrm{d} t} + L_{BA}(\theta _{r})\frac{\mathrm{d} i_{A}}{\mathrm{d} t}+i_{A}\frac{\partial L_{BA}(\theta _{r})}{\partial \theta _{r}}\frac{\mathrm{d} \theta _{r}}{\mathrm{d} t}]$

前两项是当A、B相对静止时，由电流变化引起的感应电动势——变压器电动势；

第三项是当A、B相对位置发生变化时，由于角度的变化引起的感应电动势——运动电动势。

在dt时间内输入的净电能为：

$dW_{e}=-(i_{A}e_{A}+i_{B}e_{B})dt=\psi _Adi_A+\psi _Bdi_B+2i_Ai_B\frac{\partial L_{AB}(\theta _r)}{\partial \theta _r}d\theta _r$

在dt时间内产生的机械能为：

$dW_{mech}=t_ed\theta _r=i_{A}i_{B}\frac{\partial L_{AB}(\theta _{r})}{\partial \theta _{r}}$

由此得磁场储能变化为：

$dW_{m}=dW_e-dW_{mech}=\psi _Adi_A+\psi _Bdi_B+i_Ai_B\frac{\partial L_{AB}(\theta _r)}{\partial \theta _r}d\theta _r$

分析上述公式得，所有的变压器电动势从电源吸收的能量以及运动电动势从电源吸收的能量的1/2变为了磁场储能，只有运动电动势从电源吸收的能量的剩余1/2转换为了机械功率。

所以，产生感应电动势是耦合场从电源吸收电能的必要条件；产生运动电动势是通过耦合场实现机电能量转换的关键。（磁场储能会因为定、转子的相对运动而增加，所以当电机的转速较大时容易引起电机饱和）

3 电磁转矩生成

通过上述分析，可以将电磁转矩视为由定、转子的电流相互作用生成的，其又可以看成是定、转子正弦分布径向励磁磁场相互作用的结果。（可以视为定、转子电流以及磁链相互作用的结果即载流导体在磁场中收到电磁力的作用）

电磁转矩本质上是因为定、转子磁场的相对运动，对气隙磁场即耦合场产生了扰动，使得气隙磁场的轴线发生偏移（气隙磁场发生畸变），从而产生的转矩。

电磁转矩是由于定、转子互感与相对位置有关，定、转子发生相对运动时，互感随转子角度变化，从而产生运动电动势，使得磁场储能发生变化。

3.1 转矩常数

转矩常数定义为：

$K_1\lambda _{af}=\frac{3}{2}\cdot \frac{P}{2}\lambda _{af}$

但不总是为常数，因为永磁体对温度存在敏感性，使得转子磁链不总为恒值。

4 磁阻转矩生成

对于凸极电机（气隙不均匀），磁阻转矩仅考虑定子绕组产生的气隙磁场，实际的电感变化是非正弦的，但可以仅考虑其基波分量

$L_{A}(\theta _r)=L_0+\Delta Lcos2\theta _r$

此时的磁场储能为：

$W_m=W_{m}^{'}=\frac{1}{2}L_{A}(\theta _r)i_{A}^{2}$

带入转矩求解公式得到：

$t_e=-\Delta Li_{A}^{2}sin2\theta _r=-\frac{1}{2}(L_d-L_q)i_{A}^{2}sin2\theta _r$

即使没有励磁磁场的作用，凸极转子的位置变化仍然会使气隙磁场发生畸变（本质是定子线圈自感随转子位置变化），引起磁场储能变化，产生磁阻转矩，其大小取决于dq轴电感的差值（定子电流不变时），最大转矩发生在45°，135°电角度等位置。

5 电磁转矩的控制

电机带负载的机械运动方程为（ $J$ 为系统转动惯量， $R_{\Omega }$ 为阻尼系数）：

$t_e = J\frac{\mathrm{d} \Omega _r}{\mathrm{d} t}+R_{\Omega }\Omega _r+t_L$

通常是关于 $\Omega _r$ 的非线性函数。

5.1 调速系统

电气传动对系统的转速提出控制要求，能够在一定范围内平滑地调节转速，或者能够在所需转速上稳定运行，或者能够根据指令准确完成加（减）速、起（制）动以及正（反）转等运动过程。

由机械运动方程可知，转速的控制是通过控制动转矩 $(t_e-t_L)$ 。所有只有精确地控制电磁转矩，才能构成高性能的调速系统。

5.2 伺服系统（位置随动系统）

电气传动对旋转角位移提出控制要求，主要解决位置控制问题，要求系统具有对位置指令准确跟踪的能力。

$\frac{\mathrm{d} \theta _\Omega }{\mathrm{d} t}=\Omega _r$

可将机械运动方程转化为：

$t_e=J\frac{\mathrm{d}^{2} \theta _\Omega }{\mathrm{d} t^{2}}+R_\Omega \frac{\mathrm{d} \theta _\Omega}{\mathrm{d} t}+t_L$

对电机位置的控制，同样也可以通过控制动转矩实现。

提高系统的控制性能，其前提条件和基础是提高对电磁转矩的控制品质。

6 气隙功率求电磁转矩

三相瞬时功率：

$p_{i}=v_{abc}^{t}i_{abc}=v_{as}i_{as}+v_{bs}i_{bs}+v_{cs}i_{cs}$

转子参考坐标系下的瞬时功率：

$p_{i}=\frac{3}{2}[(v_{qs}^{r}i_{qs}^{r}+v_{ds}^{r}i_{ds}^{r})+2v_{0}i_{0}]$

对于三相对称电机，不存在零序电流分量（功率等效）：

$p_{i}=\frac{3}{2}(v_{qs}^{r}i_{qs}^{r}+v_{ds}^{r}i_{ds}^{r})$

电磁转矩是最重要的输出变量，决定着电机的机械动态特性。

电磁转矩方程：

$T_e=\frac{3}{2}\frac{P}{2}[\lambda _{af}+(L_d-L_q)i_{ds}^{r}]i_{qs}^{r}$

第一项为永磁体磁链与q轴电流相互作用得到同步转矩；第二项为电机转子凸极性产生的磁阻转矩（ $t_e=-\Delta Li_{A}^{2}sin2\theta _r=-\frac{1}{2}(L_d-L_q)i_{A}^{2}sin2\theta _r$ ，将磁阻转矩的 $sin2\theta_{r}$ 分解，得到dq轴电流分量）

电磁转矩对应气隙功率，可由输入功率得到：

$P_{i}=\frac{3}{2}[v_{qs}^{r}i_{qs}^{r}+v_{ds}^{r}i_{ds}^{r}] \newline =\frac{3}{2}[R_s[(i_{qs}^{r})^{2}+(i_{ds}^{r})^{2}]+(L_qi_{qs}^{r}\frac{di_{qs}^{r}}{dt}+L_di_{ds}^{r}\frac{di_{ds}^{r}}{dt})+\omega _r(\lambda _{af}+(L_d-L_q)i_{ds}^{r})i_{qs}^{r}]$

三项分别为定子电阻损耗、磁场储能变化率、气隙功率（乘以极对数，再除以转速得到电磁转矩）。

7 稳态转矩特性

假定定子绕组中通以一组多相对称电流（dq轴电流正交）：

$\left\{\begin{matrix} I_{qs}=I_msin(\omega _rt+\delta )\\ I_{ds}=I_mcos(\omega _rt+\delta ) \end{matrix}\right.$

经过Park变换，得到转子参考坐标系下的定子电流：

$\left\{\begin{matrix} I_{qs}^{r}=I_{m}sin\delta \\ I_{ds}^{r}=I_{m}cos\delta \end{matrix}\right.$

带入转矩表达式，得到气隙转矩：

$T_e=\frac{3}{2}\frac{P}{2}[\lambda _{af}I_msin\delta +\frac{1}{2}(L_d-L_q)I_{m}^{2}sin2\delta ]$

其中 $\delta$ 成为转矩角，其直接影响气隙转矩的大小，同样包含了同步转矩和磁阻转矩，其随转矩角变化的情况如下图所示：

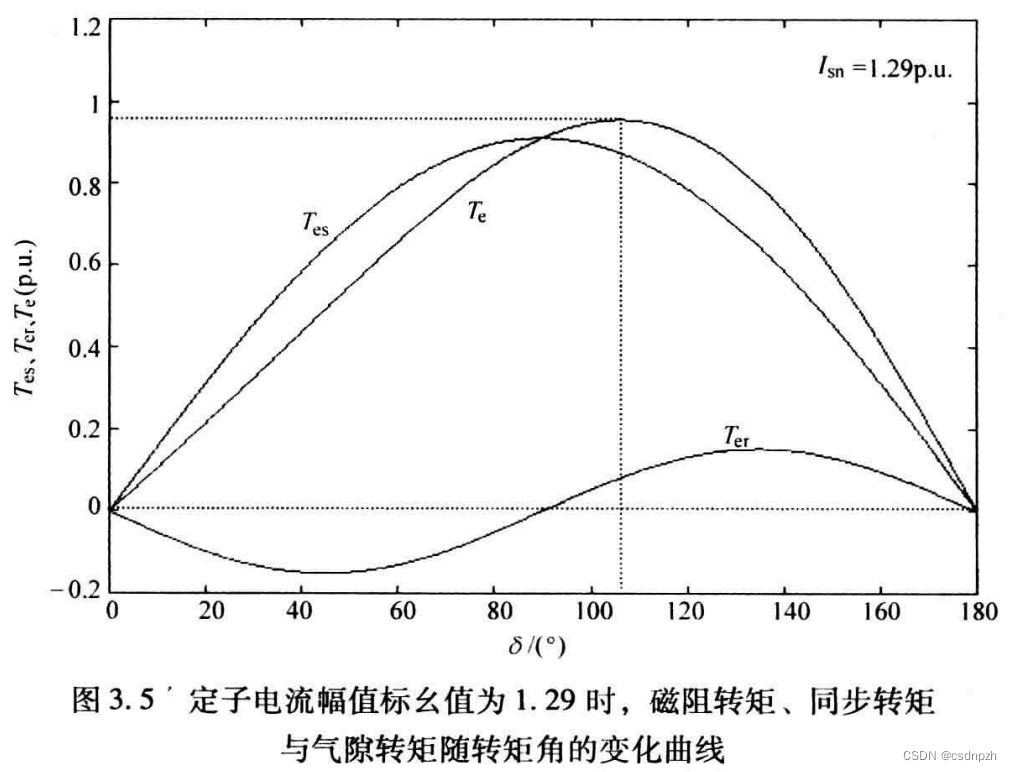
由于磁阻转矩的存在，气隙转矩将在转矩角>90°的时候达到峰值，磁阻转矩直接影响气隙转矩的峰值以及达到峰值时的转矩角。磁阻转矩在90°~180°转矩角的区间内为正值，对气隙转矩有增大的作用，反之在0°~90°转矩角的区间内为负值，对气隙转矩有削弱作用，所以一般希望转矩角工作在90°~180°的区间内。转矩角与最大转矩随定子电流幅值变化轨迹，对于电机单位电流最优转矩运行是非常重要的。

8 对于转矩的一点深入探讨

首先，转矩的大小取决于功角的大小。对于同步转矩，当功角为0~90°时，功角越大，其定、转子单位相对角度的变化引起的气隙磁场储能的变化越大，由于转矩等于气隙磁场储能随定、转子相对角度的变化，所以此时气隙转矩增大。

对于运动电动势是实现机电能量转换的关键，运动电动势与定、转子间相对角度变化的速度大小成正比，并且转换出的机械能与定、转子间的相对角度变化量有关。由于电机需要向外部做功，在无外部注入能量的情况下，将消耗动能转速将变慢。对于同步电机，即使转速达到同步转速，转子仍然在不断减速与加速，同步时定、转子无相对位置的变化，转子将没有能量注入，但是却要消耗能量对外部做功，此时转速减小，产生了运动电动势以及实现了机械能的传递，此时转矩大小仍取决于功角大小，功角大小取决于外部负载，产生的转矩对转子做功，使其加速到同步转速。稳定时此过程发生得很快，转速近乎稳定。

8.1 功角的定义

功角可以定义为主极磁场与电枢磁场的夹角（电动机），也可以定义为励磁电动势与端电压的相位角（发电机）。

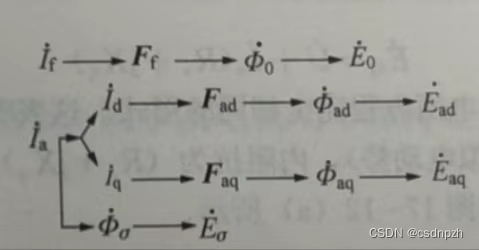
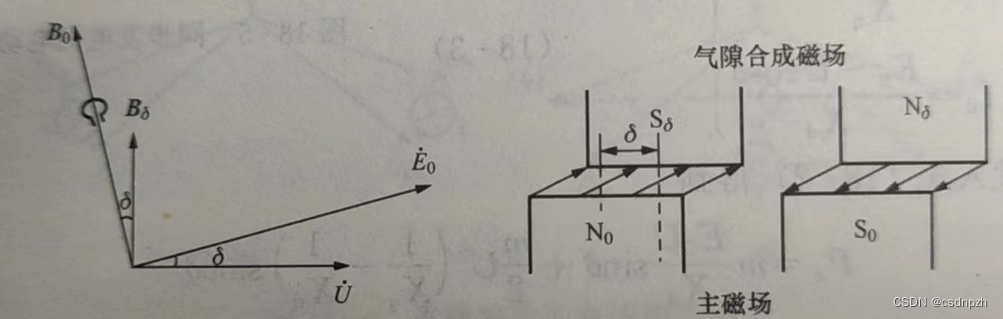
当略去定子绕组电阻和定子漏抗压降时，定子绕组的端电压近似等于各磁场在定子绕组中的感应电动势的和：

$\dot{U}=\dot{E_{0}}+\dot{E_{ad}}+\dot{E_{aq}}=\dot{E_{\delta }}$

$\dot{E_{\delta }}$ 称为气隙合成电动势，功角为 $\dot{E_{0}}$ 与 $\dot{U}$ 的相位差，可以近似认为是 $\dot{E_{\delta }}$ 与 $\dot{E_{0}}$ 的夹角， $\dot{E_{0}}$ 由主极磁场产生， $\dot{E_{\delta }}$ 由气隙合成磁场产生，于是功角可以近似认为是主极磁场与气隙合成磁场之间的夹角。

8.2 电枢反应

对于发电机，交磁电枢反应，产生的感应电流与感应电动势同相的分量，产生的磁动势与主磁极产生一定夹角，于是产生了转矩；与主磁通同相或反相的部分产生与主磁通同相或反相的磁场，增加或减小了磁场储能。机械能的输入，是为了维持电流输出，克服电枢上的电阻电抗等负载，产生端电压U。同时产生的电流对应的磁场不仅消耗机械能，并且可能会削弱或者增强气隙磁场。

对于电动机，输入变化电压，产生变化电流，并产生变压器电动势，电流的交轴分量产生的磁场对转子产生驱动，输出机械能。并且直轴分量改变磁场储能。由于不同电动势对应的电流不同，分别都需要产生与电动势产生功率消耗，也就需要外部电压不断输入电能，并且需要不断变化的电流产生变化的磁场一部分用于传递机械能，另一部分用于改变磁场储能。（感应电动势是顺便产生的，本质上需要由电流产生磁通，感应电动势可以表征需要的能量）。