三相永磁同步电机之三：动态模型

最新推荐文章于 2025-08-27 08:16:50 发布

原创最新推荐文章于 2025-08-27 08:16:50 发布 · 1.6k 阅读

19 ·

CC 4.0 BY-SA版权

文章标签：

#python

电机专栏收录该内容

3 篇文章

订阅专栏

1 概述

永磁同步电机调速驱动通过变换器供电，由于收到开关功率等级以及滤波器尺寸等因素的限制，供电方式只能是有限电源，缺乏提供瞬态大功率的能力。因此需要评价变换器供电的调速驱动器的动态性能以确定开关器件等级及适用于给定电机的变换器，最终由变换器和电机的相互作用来确定系统电流。其中使用的动态模型常用于评价当电压/电流、定子频率发生变化及转矩产生扰动时对系统产生的瞬时影响。

永磁同步电机的动态模型可由绕组位于dq轴的两相电机推导而来，定子上进存在一套两个绕组，转子上不存在绕组仅有永磁体，永磁体可由电流源模型或磁链源模型等效。但是由于定子电感会随转子转动而变化，静态坐标系不利于动态分析，可将静止dq坐标系转换为旋转dq坐标系随转子同步旋转，从而使得电感变为常值。动态模型的建立过程如下图所示：

2 两相永磁同步电机的实时模型

2.1 动态模型假设

1.定子绕组加以对称正弦分布的磁动势

2.电感随转子位置正弦变化

3.饱和及参数变化忽略不计

2.2 实时模型

2.2.1 定子电压方程（两相静止坐标系下）

可由定子电阻的电压降和磁链的微分（电磁感应定律）之和求得：

$\left\{\begin{matrix} v_{qs} = R_{q}i_{qs}+\frac{d\lambda _{qs}}{dt}\\ v_{ds} = R_{d}i_{ds}+\frac{d\lambda _{ds}}{dt} \end{matrix}\right.$

定子dq轴磁链包括自感磁链、互感磁链以及永磁体磁链 $\lambda_{af}$ ：

$\left\{\begin{matrix} \lambda_{qs}=L_{qq}i_{qs}+L_{qd}i_{ds}+\lambda_{af}sin\theta_{r}\\ \lambda_{ds}=L_{dd}i_{ds}+L_{dq}i_{qs}+\lambda_{af}cos\theta_{r} \end{matrix}\right.$

由于绕组对称，绕组电阻相等 $R_{s}=R_{d}=R_{q}$ ，由于dq轴绕组对称因此互感也相等，磁链方程带入电压方程可得：

$\left\{\begin{matrix} v_{qs} = R_{s}i_{qs}+i_{qs}\frac{dL_{qq}}{dt} + L_{qq}\frac{di_{qs}}{dt}+i_{ds}\frac{dL_{qd}}{dt}+L_{qd}\frac{di_{ds}}{dt}+\lambda_{af}\frac{dsin\theta _{r}}{dt}\\ v_{ds} = R_{d}i_{ds}+i_{ds}\frac{dL_{dd}}{dt} + L_{dd}\frac{di_{ds}}{dt}+i_{qs}\frac{dL_{dq}}{dt}+L_{dq}\frac{di_{qs}}{dt}+\lambda_{af}\frac{dcos\theta _{r}}{dt}\\ \end{matrix}\right.$

将电感方程（参考电感那篇文章）带入电机电压方程中：

$\begin{bmatrix} v_{qs}\\ v_{ds} \end{bmatrix} =R_{s}\begin{bmatrix} i_{qs}\\ i_{ds} \end{bmatrix} +\begin{bmatrix} L_{0}+\Delta Lcos(2\theta_r) & -\Delta Lsin(2\theta_r)\\ -\Delta Lsin(2\theta_r) & L_{0}-\Delta Lcos(2\theta_r) \end{bmatrix} \frac{d}{dt}\begin{bmatrix} i_{qs}\\ i_{ds} \end{bmatrix} +2\omega_{r}\Delta L\begin{bmatrix} -sin2\theta_{r} & -cos2\theta_{r}\\ -cos2\theta_{r} & sin2\theta_{r} \end{bmatrix} \begin{bmatrix} i_{qs}\\ i_{ds} \end{bmatrix} +\lambda_{af}\omega_{r}\begin{bmatrix} cos\theta_{r}\\ -sin\theta_{r} \end{bmatrix}$

当电机不存在凸极性，即表贴式电机， $L_{d}=L_{q}$ 时，第三项不存在，电感的波动也不存在，得到表贴式永磁同步电机的电压方程：

$\begin{bmatrix} v_{qs}\\ v_{ds} \end{bmatrix} =R_{s}\begin{bmatrix} i_{qs}\\ i_{ds} \end{bmatrix} +\begin{bmatrix} L_{0} & 0\\ 0 & L_{0} \end{bmatrix} \frac{d}{dt}\begin{bmatrix} i_{qs}\\ i_{ds} \end{bmatrix} +\lambda_{af}\omega_{r}\begin{bmatrix} cos\theta_{r}\\ -sin\theta_{r} \end{bmatrix}$

2.2.2 定子磁链方程

将上述定子磁链方程的谐波分量写为矩阵形式（方程中的永磁体产生的磁链仅考虑基波分量）：

$\begin{bmatrix} \lambda_{qsi}\\ \lambda_{dsi} \end{bmatrix} = \begin{bmatrix} L_{qq} & L_{qd}\\ L_{dq} & L_{dd} \end{bmatrix} \begin{bmatrix} i_{qsi}\\ i_{dsi} \end{bmatrix} = \begin{bmatrix} L_{0} + \Delta Lcos2\theta_{r} & -\Delta Lsin2\theta_{r}\\ -\Delta Lsin2\theta_{r} & L_{0} - \Delta Lcos2\theta_{r} \end{bmatrix} \begin{bmatrix} i_{qsi}\\ i_{dsi} \end{bmatrix}$

该方程仅用于电机在线性区域运行时使用，如果电机工作在饱和区则叠加原理将不再使用，所以一般需要将电机的运行区限定在线性工作区域（在达到额定电流之前均为线性，因为永磁同步电机气隙较大且永磁体也可视为等效气隙，磁阻较大，不易使铁芯饱和）。

注意：磁链与电流的关系包含转子位置项，因此可以通过给定注入电流，在已知磁链的情况下估计出转子位置。目前通过注入信号或间接测量电感而依赖响应磁链方程来解算转子位置的研究收到重视——无位置传感器控制。

2.3 转子参考坐标系的建立

通过建立一个旋转速度与正弦变量的角速度一致的参考坐标系，此时在该旋转坐标系中观测到的该正弦量为直流信号。并且从旋转坐标系上看，系统的电感矩阵不再依赖于转子位置，简化了系统方程。变换前后的坐标系关系如下图所示（本质上就是Park变换）：

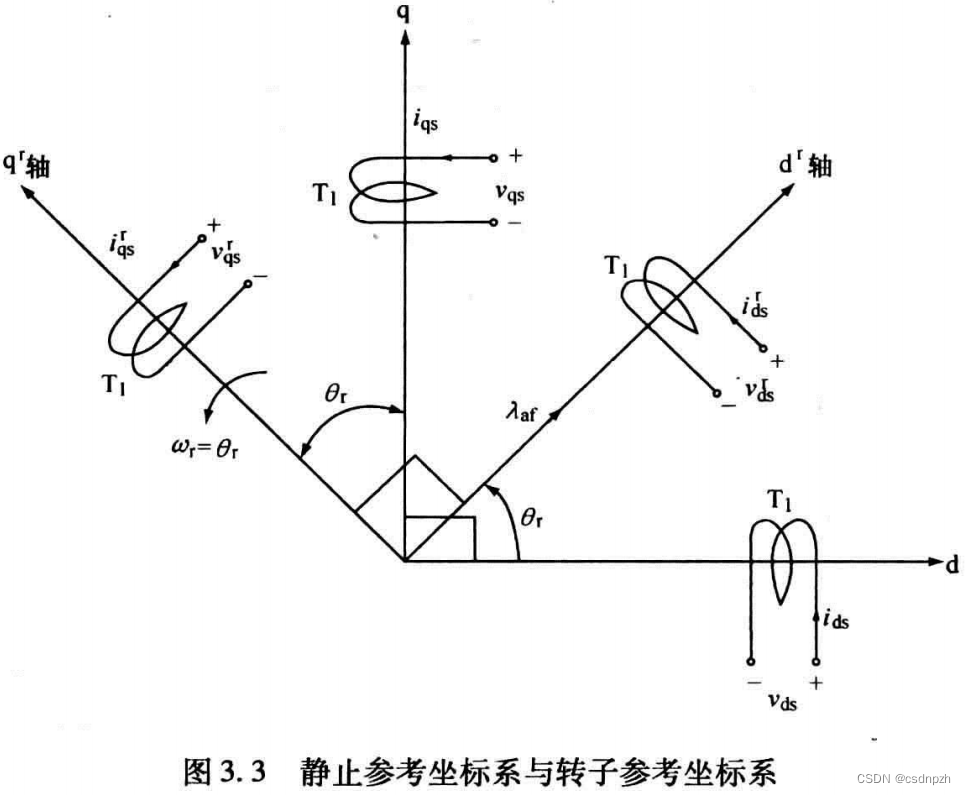
此时产生的虚拟定子线圈是以转子的角速度旋转的，此时旋转dq轴上的电感就是固定不变的，分别为 $L_{d},L_{q}$ 。同时将电压与电流进行Park变换得到转子参考坐标系下的永磁同步电机电压方程为（注意要先进行Park变换再求导）：

$\begin{bmatrix} v_{qs}^{r}\\ v_{ds}^{r} \end{bmatrix} =\begin{bmatrix} R_{s}+L_{q}\frac{d}{dt} & \omega_{r}L_{d}\\ -\omega_{r}L_{q}& R_{s}+L_{d}\frac{d}{dt} \end{bmatrix}\begin{bmatrix} i_{qs}^{r}\\ i_{ds}^{r} \end{bmatrix} +\begin{bmatrix} \omega_{r}\lambda_{af}\\ 0 \end{bmatrix}$

表示为阻抗矩阵与电流矢量的乘积+转子磁链产生的运动反电动势分量。仅当速度恒定的稳态时系统方程才是线性的，如果转子速度变化是由于定子电流变化引起的，那么系统方程将变为非线性的。

注意：稳态正弦输入的情况下， $\frac{di}{dt}=j\omega \cdot i$ ， $j$ 表示相位的变化（在复平面上逆时针旋转90°），此时 $\omega L$ 为感抗。当转速恒定时，转子参考坐标系的电流视为直流量，对其微分为0。

2.3.1 三相静止坐标系到转子坐标系的变换

通过Clark变换，即可将三相静止坐标系转换到转子坐标系：

$T_{3s->2r}=T_{2s-2r}\cdot T_{3s-2s}=\frac{2}{3}\begin{bmatrix} cos\theta_{r} & cos(\theta_{r} - \frac{2\pi }{3}) & cos(\theta_{r} + \frac{2\pi }{3})\\ sin\theta_{r} & sin(\theta_{r}-\frac{2\pi }{3}) & sin(\theta_{r}+\frac{2\pi }{3})\\ \frac{1}{2} & \frac{1}{2} & \frac{1}{2} \end{bmatrix}$

当三相电流或电压不对称时，将产生零序分量，零序电流不产生合成磁场。如果三个变量之间存在内在联系，比如相同的相位差和相等的幅值，那么就可以降阶为两个变量之间的关系，即只有两个变量时独立的。否则，三个变量不独立，存在零序分量。

2.3.2 不对称运行

当三相绕组中通以不对称的电流或电压时，三相电流间的内在关系将不再成立即三相电流在同一时刻的代数和为0不成立。零序电压：

$v_{0}=R_{s}i_{0}+\frac{d\lambda_{0}}{dt} =R_{s}i_{0}+L_{0}\frac{di_{0}}{dt}$

3 磁链模型

永磁同步电机动态方程使用磁链作为变量，其优点在于对这些变量进行微分具有较好的数值稳定性，因为即使电压和电流不连续时，磁链仍然是连续的。运用磁链表示法可以突出永磁同步电机中磁通与转矩的解耦过程。

转子参考坐标系下的磁链为：

$\left\{\begin{matrix} \lambda_{qs}^{r}=L_qi_{qs}^{r}\\ \lambda_{ds}^{r}=L_di_{ds}^{r}+\lambda _{af} \end{matrix}\right.$

将电流使用电感和磁链表示的定子电压方程：

$\left\{\begin{matrix} v_{qs}^{r}=\frac{R_s}{L_q}\lambda_{qs}^{r}+\frac{\mathrm{d} \lambda_{qs}^{r}}{\mathrm{d} t}+\omega _r\lambda _{ds}^{r}+\omega _r\lambda _{af}\\ v_{ds}^{r}=\frac{R_s}{L_q}\lambda_{qs}^{r}+\frac{\mathrm{d} \lambda_{ds}^{r}}{\mathrm{d} t}-\omega _r\lambda _{qs}^{r} \end{matrix}\right.$

电磁转矩公式转换为磁链形式：

$T_e=\frac{3}{2}\frac{P}{2}\frac{1}{L_q}[\rho \lambda _{af}+(1-\rho )\lambda _{ds}^{r}]\lambda _{qs}^{r} \newline =\frac{3}{2}\frac{P}{2}[\lambda _{ds}^{r}i_{qs}^{r}-\lambda _{qs}^{r}i_{ds}^{r}]$