三相永磁同步电机之四：电感

最新推荐文章于 2025-09-06 23:11:56 发布

原创最新推荐文章于 2025-09-06 23:11:56 发布 · 2.4k 阅读

15 ·

CC 4.0 BY-SA版权

文章标签：

#python

电机专栏收录该内容

3 篇文章

订阅专栏

1 电感定义

一般电路中的电感指的是单位电流变化产生感应电动势的能力：

$e = L\frac{di}{dt}$

在电机中引入了磁链的概念，其定义为线圈匝数乘以线圈磁通：

$\psi =N\phi$

为了表征单位电流产生磁链的能力，于是引入了磁路中的电感概念：

$L_{m} = \frac{\psi }{i}$

其于电路中电感的量纲相同，均为H。

2 电机电感的推导

首先当线圈中通入电流 $i$ 时，线圈将在磁路中产生磁动势 $f$ ，磁动势随之在磁路中产生磁通 $\phi$ ，磁通的大小取决于磁路的磁阻大小 $R_{m}$ ，由于磁链 $\psi$ 与磁通关于线圈匝数成正比，所以磁链自然与线圈中通入的电流成正比，并且与磁路的磁阻成反比。

$f = Ni$

$f = \phi R_{m}$

$\phi R_{m}=Ni$

$\psi =N\phi =\frac{N^{2}i}{R_{m}}$

$L_{m}=\frac{\psi }{i}=\frac{N^{2}}{R_{m}}$

3 dq轴电感

在静止的定子dq坐标系中，当转子的磁极轴线与定子的d轴重合时，永磁体磁极正对d轴线圈（定子的dq轴线圈是通过Clark变换等效的），如下图所示（夹角为45°电角度的情况）：

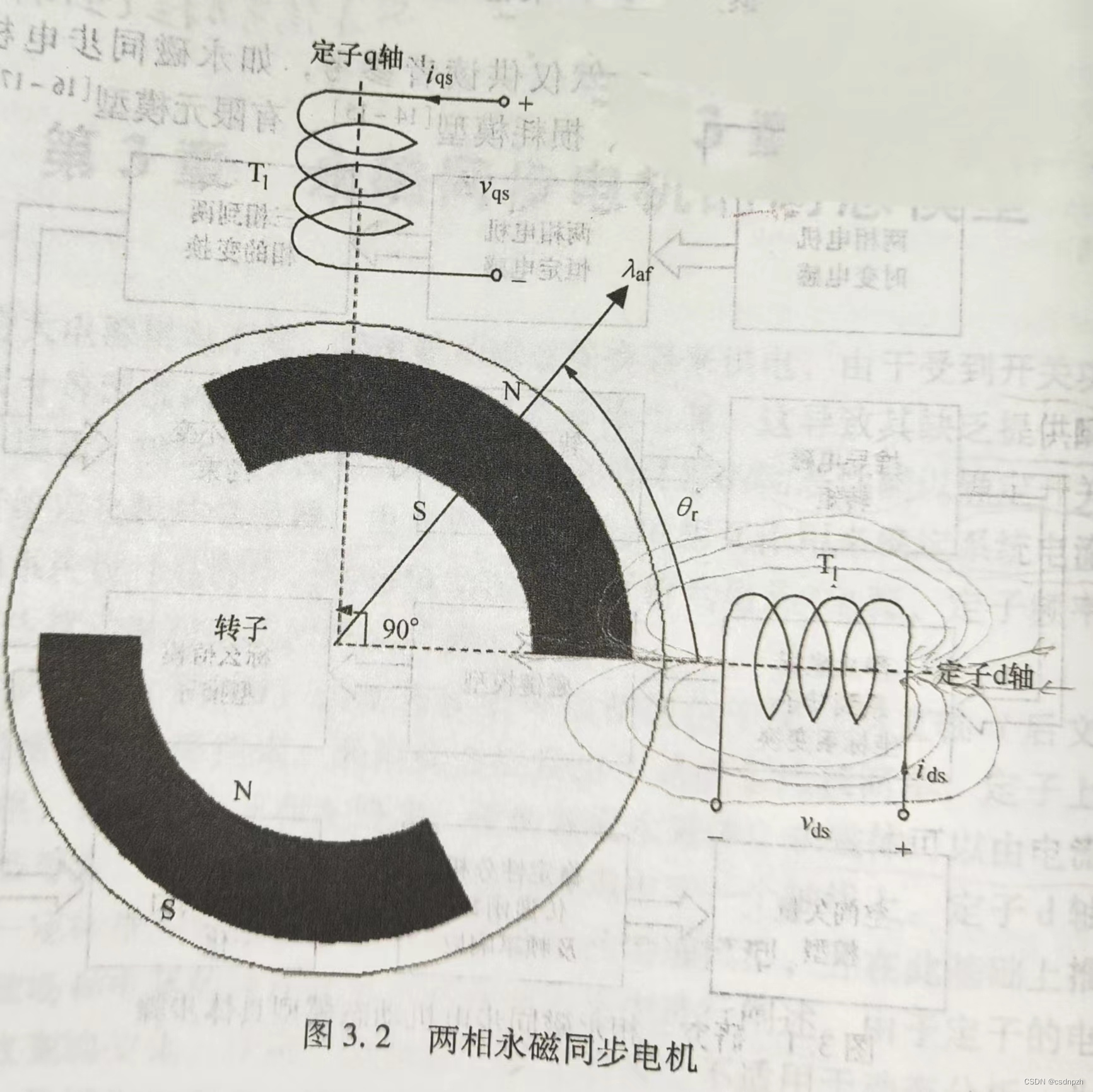
此时定子d轴线圈产生的磁场几乎全部穿过永磁体，对于内置式永磁同步电机（凸极电机）而言，因永磁体的相对磁导率接近空气，而转子铁芯的磁导率可视为无穷大，磁路的磁阻是所有时刻最大所以此时定子d轴线圈的，即磁路的电感最小定义为 $L_{d}$ ，当转子磁极轴线转过90°电角度与定子d轴垂直时，此时定子d轴产生的大部分磁场都不穿过永磁体，此时磁路的磁阻最小，即磁路的电感最大定义为 $L_{q}$ 。

4 dq轴电感表达式（两相静止坐标系下）

由于定子dq轴电感的变化频率与转子极数对应，是转子转频的2倍，假设绕组的磁动势分布是正弦的，于是自感可以表示为位置角的余弦函数，dq轴自感空间相位相差90度电角度：

$\left\{\begin{matrix} L_{qq}=\frac{1}{2}[(L_{q}+L_{d})+(L_{q}-L_{d})cos(2\theta_{r})]\\ L_{dd}=\frac{1}{2}[(L_{q}+L_{d})-(L_{q}-L_{d})cos(2\theta_{r})] \end{matrix}\right.$