HDU 1494 跑跑卡丁车

传送门

多阶段决策dp。
这道题题意上需要注意两点：（这两点都与实际游戏相悖，这题出的那年06年我就在玩了）

1. 加速行驶的那一段赛道是不会获得能量的。
2. 可以认为，判断当前是否废掉一个能量槽（触发条件：当前赛道普通行驶 且 上一段赛道末尾能量值为14，则直接减去4(+1-5)点能量）是在当前赛道的末尾进行的，而下一段赛道是否使用加速卡也是在下一段赛道的末尾进行的。
   也就是说，不允许有那种极限操作（当前已有两个加速且能量刚满，然后瞬间使用一个加速且又得到一个加速，没有任何浪费）。

这道题我想到了用dp[100*100][15]这样来表示状态。但是没注意到以上两点。由以上可知，每段末尾的能量值可以是0，最多是14，不能有15的情况（出现15瞬间变为10）。

由此得知，每段赛道只有在自己赛道末尾这个时机去更新当前能量值，且只关心自己这段赛道的情况。更新只有三种情况，-5（当前使用加速了）或+1（当前没使用加速）或-4（当前没加速，因为卡槽和能量槽都满了所以废掉能量槽）。
所以，dp[i][j]表示从起点行驶到第i段赛道末尾（已更新能量值），当前的能量值为j的情况下的最短用时。

由此可以设计出状态转移。必须注意数组越界的情况，而且这些情况往往意味着无效状态（但无效状态可能并不止这些），所以j==0和j>9的情况都只对应着当前赛道一定加速和一定没加速。但别忘了j==10还有可能来源于能量废掉。

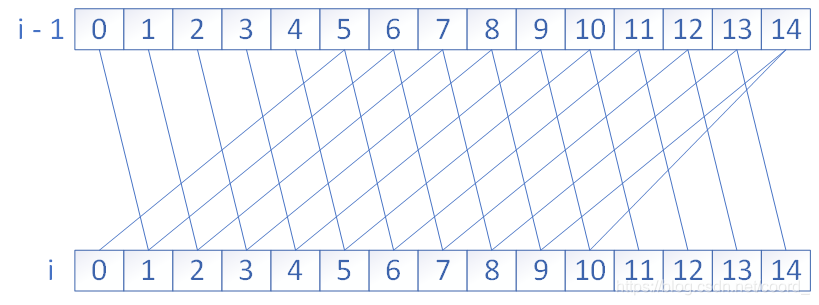
其实还有很多状态是非法的，比如dp[0][1],dp[1][2],dp[2][1]这些，说不完的，但至少可以保证数组不越界了。这些为什么不会出幺蛾子？其实可以这样想：我先把dp全部弄成INF（因为取最小），然后把唯一的初始状态dp[0][0]=0设为合法，可以想到“通过合法状态转移到的状态都是合法状态（体会下图）”，所以其逆否命题也成立（非法状态一定由非法状态得到）。

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <vector>
#include <cstring>
#include <string>
#include <queue>
using namespace std;

const int INF = 0x3f3f3f3f;
int L, N;

int A[10000], B[10000];
int dp[10000][15];               //
int ans;

void init()
{
	memset(dp, 0x3f, sizeof dp);
	dp[0][0] = 0;
	ans = INF;
}

int main()
{
	for (; ~scanf("%d%d", &L, &N);)
	{
		init();
		for (int i = 1; i <= L; i++)
			scanf("%d", &A[i]);
		for (int i = 1; i <= L; i++)
			scanf("%d", &B[i]);

		N *= L;
		A[0] = A[L];                          // 这里很重要。模L的结果是0~L-1，而下标为0的值没有被赋予
		B[0] = B[L];
		for (int i = L + 1; i <= N; i++)
		{
			A[i] = A[i%L];
			B[i] = B[i%L];
		}
		for (int i = 1; i <= N; i++)
		{
			for (int j = 0; j <= 14; j++)
			{
				if (j == 0) dp[i][j] = dp[i - 1][j + 5] + B[i];
				else if (j > 10) dp[i][j] = dp[i - 1][j - 1] + A[i];
				else if (j == 10) dp[i][j] = min(dp[i - 1][j - 1] + A[i], dp[i - 1][14] + A[i]);    //
				else dp[i][j] = min(dp[i - 1][j - 1] + A[i], dp[i - 1][j + 5] + B[i]);
			}
		}
		for (int j = 0; j <= 14; j++)
			ans = min(ans, dp[N][j]);
		printf("%d\n", ans);
	}

	return 0;
}

/*    如果你觉得dp[x][y]一定小于dp[x][y+z] (z>0)，可以试试这个例子（样例去掉了最后一段），让最后的每个dp[N][j]都输出出来
17 1
9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9 9
8 8 8 8 8 8 8 8 8 8 8 8 8 8 1 1 8
*/