何为二分?形象的说,就是单调函数求零点。
我们先对二分查找简单的分析一下(主要是模板及易错点)
1.找>=x的第一个位置: 2.找<=x的第一个位置:
while(l<r){ while(l<r){
mid=(l+r)/2; mid=(l+r)/2;
if(a[mid]>=x) r=mid; if(a[mid]<=x) l=mid;
else l=mid+1; else r=mid-1;}
}
首先,对于代码1,当mid的值大于等于x时,说明mid后面都不是目标值但自己不确定。
而当mid的值小于x时,说明mid自己及其前面都不是目标值。
所以l到r的区间即为目标值存在的区间,所以只要保证两者稳定的逼近一个点即可。
当区间不断变小时,对于代码2,因为mid的向左取整,而l又直接赋值为mid,于是可能会进入死循环。而1的话l再mid基础上加了1,保证它至少会走1步,避免了死循环。
所以代码2只需mid=(l+r+1)/2即可。或者把循环条件改为l<=r,l=mid+1;这样就能保证不会陷入死循环,不过这样答案在l-1上。
因此,法1可以改成:l<=r,r=mid-1;
这样子,r及其后面一个都可能为答案,而终止时l==r+1;因此l所在的地方即为答案。
特别的当r不动时,l一定与R会相等,如果此时r还是不动,说明无法找到,l也指向右边界+1;
注意一点细节:
有时+r可能会超int ,我们可以用l+(r-l)/2来代替。
C++ STL的二分查找函数:
binary_search:返回bool是否存在
lower_bound:返回第一个符合条件的位置 1 2 3 5 6 7,搜4时指向5
upper_bound:返回最后一个符合条件的位置 1 2 2 3 3 5,插3时指向5
下面来一道水题:
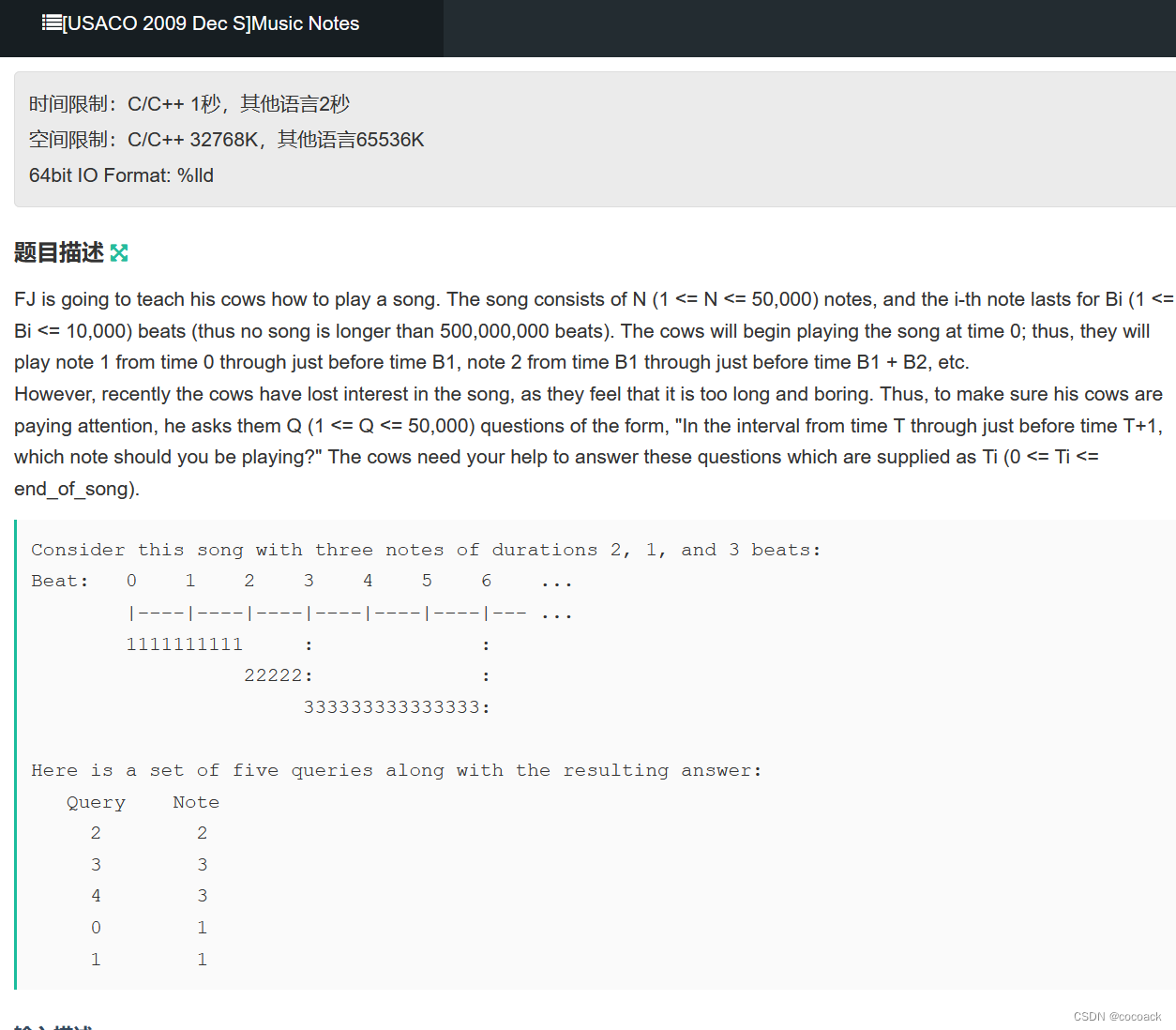
我们用前缀和维护并分别用二分即可,下面是AC代码:





 本文详细介绍了二分查找的工作原理,强调了代码实现中的模板分析和易错点,以及C++STL中`binary_search`、`lower_bound`和`upper_bound`函数的应用。通过实例演示如何避免死循环并优化二分查找算法。
本文详细介绍了二分查找的工作原理,强调了代码实现中的模板分析和易错点,以及C++STL中`binary_search`、`lower_bound`和`upper_bound`函数的应用。通过实例演示如何避免死循环并优化二分查找算法。
















 523
523










