hihoCoder Challenge 29 D. 不上升序列【动态规划+折线+堆】

题目大意：

给出一个整数序列，可以花费1的代价把一个数+1或­1，求把它变成不上升序列的最小代价。n<=500000;

解题思路：

令 $f_i(x)$ 为前个数，调整出最大值不超过 $x$ 的最小代价,那么 $f_i$ 是一条不升的折线
考虑转移 $f_i(x)=\text{min}_{y\le x}f_{i-1}(y)+|a_i-y|$
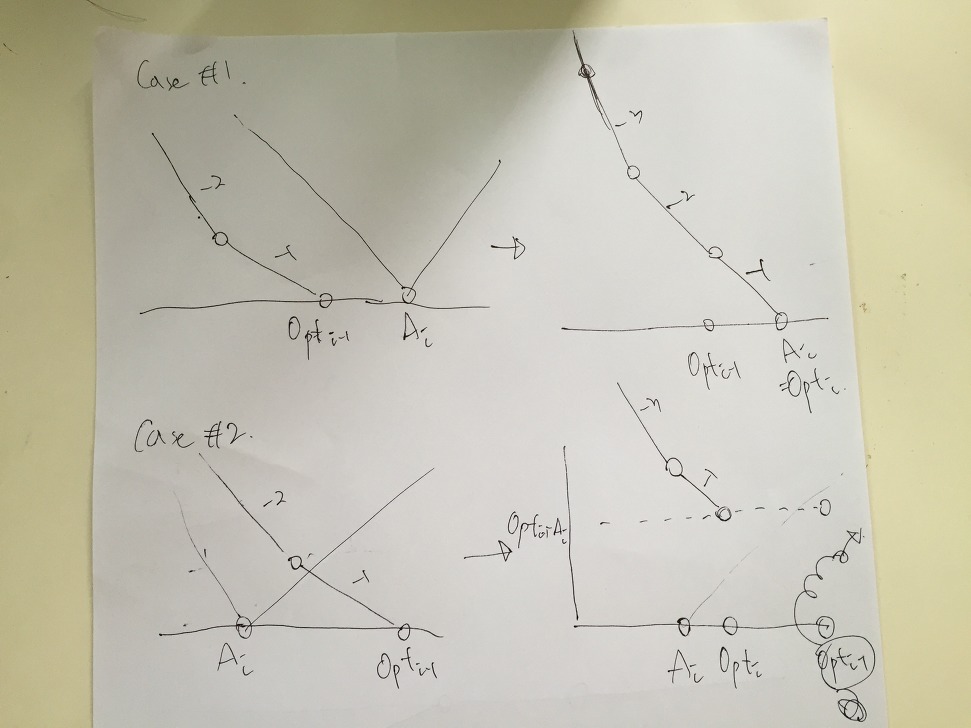
这实际上是两条折线合并一下 我们讨论两者的位置关系
先加一个下凸折线，再取个前缀min 。
取前缀min,就是把斜率>=1的部分删掉，实现的话只需要在堆中记下所有的折点。
附一张题解的图方便理解：

#include<bits/stdc++.h>
#define ll long long
using namespace std;
int getint()
{
    int i=0,f=1;char c;
    for(c=getchar();(c!='-')&&(c<'0'||c>'9');c=getchar());
    if(c=='-')c=getchar(),f=-1;
    for(;c>='0'&&c<='9';c=getchar())i=(i<<3)+(i<<1)+c-'0';
    return i*f;
}
priority_queue<int>q;
int main()
{
    //freopen("lx.in","r",stdin);
    int n=getint(),x;ll ans=0;
    for(int i=1;i<=n;i++)
    {
        x=-getint();q.push(x);
        if(q.top()>x)ans+=q.top()-x,q.pop(),q.push(x);
    }
    cout<<ans<<'\n';
}