基于深度学习CsiNet-LSTM的信道状态反馈网络模型研究

最新推荐文章于 2025-12-20 21:22:01 发布

原创最新推荐文章于 2025-12-20 21:22:01 发布 · 976 阅读

12 ·

CC 4.0 BY-SA版权

文章标签：

#深度学习 #lstm #人工智能 #CsiNet-LSTM #信道状态反馈网络

智能通信技术专栏收录该内容

9 篇文章

订阅专栏

该文章已生成可运行项目，

CsiNet-LSTM模型在CsiNet基础上引入长短期记忆网络（LSTM），通过融合空间特征与时间序列信息，提升动态信道下的反馈精度与鲁棒性。其核心思想是：利用编码器压缩当前CSI的空间特征，同时通过LSTM挖掘历史CSI的时间关联性，解码器结合空间压缩特征与时间依赖信息重构 CSI，实现低开销、高精度的动态信道反馈。

1.CsiNet-LSTM模型原理

CsiNet-LSTM的整体架构分为编码器(Encoder)、LSTM时间序列处理器和解码器(Decoder)三部分，CsiNet-LSTM整体架构如下图所示：

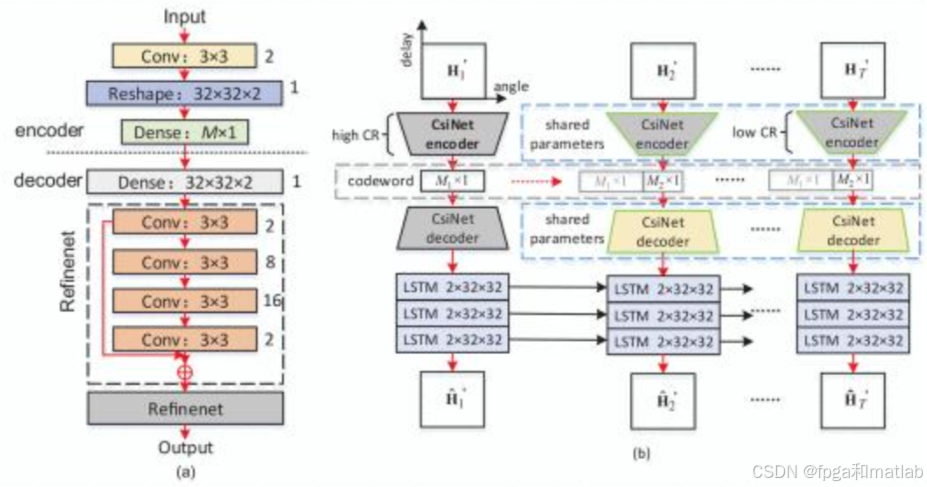
具体原理如下：

空间特征提取与压缩(编码器)无线CSI通常以复数矩阵形式表示(如MIMO系统中的信道矩阵)，包含丰富的空间域信息(如路径损耗、多径效应)。编码器通过卷积神经网络(CNN)提取CSI的空间特征，并将高维CSI矩阵压缩为低维反馈向量，降低传输开销。

时间依赖建模(LSTM模块)无线信道具有时间连续性(如车辆移动场景下的信道变化)，历史CSI包含当前信道的演化趋势信息。LSTM模块通过记忆单元捕捉历史CSI的时间序列特征，生成时间关联向量，辅助当前CSI的重构。

CSI重构(解码器)解码器将编码器输出的空间压缩向量与LSTM输出的时间关联向量融合，通过反卷积操作重构高维CSI矩阵，实现高精度恢复。

1.1 编码器——空间特征压缩

编码器由3层卷积层(Conv)和1层全连接层(FC)组成，逐步提取空间特征并压缩维度：

第1卷积层

第2卷积层

第3卷积层

全连接压缩层

1.2 LSTM时间序列处理模型

LSTM模块输入历史T个时刻的压缩向量{zt−T,…,zt−1}，输出当前时刻的时间关联向量ht，具体计算如下：

遗忘门

输入门

细胞状态更新

输出门

1.3 解码器——CSI重构

解码器将编码器输出的zt与LSTM输出的ht融合，通过反卷积重构CSI：

特征融合

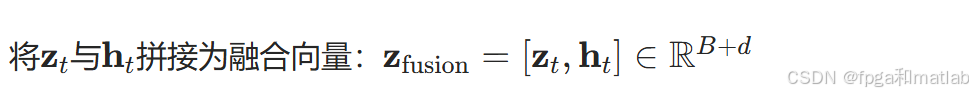
全连接扩展层

第1反卷积层

第2反卷积层

输出层

复数转换

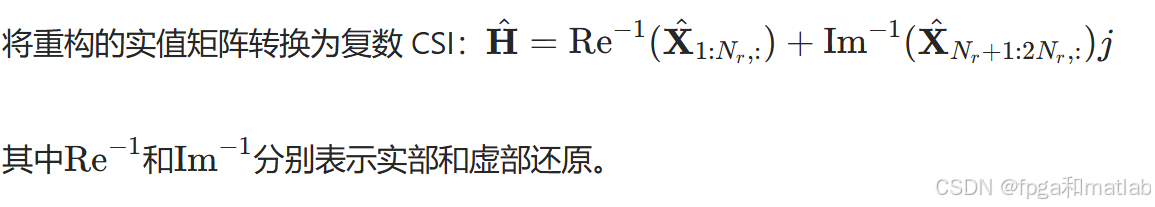
2.CsiNet-LSTM网络模型的训练

采用均方误差(MSE)衡量重构CSI与原始CSI的差异：

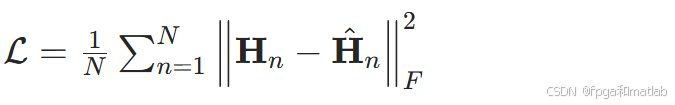
其中N为训练样本数，∥⋅∥F为Frobenius范数。

使用Adam优化器最小化损失函数，更新参数：

其中θ为模型所有参数(卷积核、偏置、LSTM权重等)，η为学习率，∇θL为参数的梯度。

3.matlab核心程序

% 基于深度学习的CsiNet-LSTM信道状态反馈网络模型
% 适用场景：MIMO系统信道状态信息(CSI)压缩反馈
% 版本：MATLAB R2023a及以上（需Deep Learning Toolbox）

clear; clc; close all;
rng(0);  % 固定随机种子，保证结果可复现


%% 1. 数据准备与预处理
% 1.1 生成模拟CSI数据（实际应用中可替换为实测数据）
% 设定MIMO系统参数：Nr=32接收天线，Nt=32发射天线，采样点数=10000，时间序列长度=10
Nr = 32;         % 接收天线数
Nt = 32;         % 发射天线数
numSamples = 10000;  % 总样本数
timeSteps = 10;   % 时间序列长度（每个样本包含10个时间步的CSI）

% 生成复信道矩阵H：Nr×Nt×timeSteps×numSamples（复数）
% 模拟瑞利衰落信道，加入时间相关性（相邻时间步相关系数0.8）
H = zeros(Nr, Nt, timeSteps, numSamples);
for s = 1:numSamples
    % 初始时间步信道（瑞利分布）
    H(:, :, 1, s) = (randn(Nr, Nt) + 1i*randn(Nr, Nt))/sqrt(2);
    % 后续时间步（基于前一时间步添加高斯噪声，模拟时间相关性）
    for t = 2:timeSteps
        H(:, :, t, s) = 0.8*H(:, :, t-1, s) + 0.6*(randn(Nr, Nt) + 1i*randn(Nr, Nt))/sqrt(2);
    end
end

% 1.2 数据格式转换：复数→实值矩阵（实部+虚部拼接）
% 输入维度：(2*Nr)×Nt×timeSteps×numSamples（实值）
X = zeros(2*Nr, Nt, timeSteps, numSamples);
for s = 1:numSamples
    for t = 1:timeSteps
        X(:, :, t, s) = [real(H(:, :, t, s)); imag(H(:, :, t, s))];  % 实部在上，虚部在下
    end
end

% 1.3 归一化处理（按样本维度标准化）
X_mean = mean(X, 4);  % 计算均值（沿样本维度）
X_std = std(X, [], 4) + 1e-8;  % 计算标准差（加小值避免除零）
X_norm = (X - X_mean) ./ X_std;  % 归一化到N(0,1)

% 1.4 划分训练集、验证集、测试集（7:1:2）
trainIdx = 1:7000;
valIdx = 7001:8000;
testIdx = 8001:10000;

X_train = X_norm(:, :, :, trainIdx);
X_val = X_norm(:, :, :, valIdx);
X_test = X_norm(:, :, :, testIdx);

% 标签与输入相同（自编码器任务：重构输入）
Y_train = X_train;
Y_val = X_val;
Y_test = X_test;


%% 2. 模型构建：CsiNet-LSTM（编码器+LSTM时间处理器+解码器）
% 2.1 超参数设置
feedbackBits = 128;  % 反馈比特数（压缩向量长度）
lstmHiddenSize = 64; % LSTM隐藏层维度
numFilters = [32, 64, 128];  % 卷积层滤波器数量
filterSize = [3, 3, 3];      % 卷积核尺寸
stride = [1, 1, 1];          % 卷积步长

% 2.2 编码器（空间特征提取与压缩）
encoderInput = sequenceInputLayer([2*Nr, Nt, 1], 'Name', 'encoder_input');  % 输入层（含时间序列）

% 卷积层1：提取低级空间特征
conv1 = convolution2dLayer(filterSize(1), numFilters(1), ...
    'Stride', stride(1), 'Padding', 'same', 'Name', 'conv1');
relu1 = reluLayer('Name', 'relu1');

% 卷积层2：提取中级空间特征
conv2 = convolution2dLayer(filterSize(2), numFilters(2), ...
    'Stride', stride(2), 'Padding', 'same', 'Name', 'conv2');
relu2 = reluLayer('Name', 'relu2');

% 卷积层3：提取高级空间特征
conv3 = convolution2dLayer(filterSize(3), numFilters(3), ...
    'Stride', stride(3), 'Padding', 'same', 'Name', 'conv3');
relu3 = reluLayer('Name', 'relu3');

% 全连接层：压缩为反馈向量（长度=feedbackBits）
% 先计算卷积输出的扁平化维度
conv3OutputSize = [2*Nr, Nt, numFilters(3)];  % 卷积3输出尺寸（因Padding='same'）
flattenSize = prod(conv3OutputSize);          % 扁平化后维度
fcCompress = fullyConnectedLayer(feedbackBits, 'Name', 'fc_compress');

% 编码器层序列
encoderLayers = [
    encoderInput
    conv1
    relu1
    conv2
    relu2
    conv3
    relu3
    flattenLayer('Name', 'flatten')  % 展平特征图
    fcCompress
];

% 2.3 LSTM时间序列处理器（建模时间相关性）
% LSTM层：输入为编码器输出的反馈向量序列
lstmLayer = lstmLayer(lstmHiddenSize, ...
    'OutputMode', 'sequence', ...  输出每个时间步的隐藏状态
    'Name', 'lstm_time');

% 2.4 解码器（融合时空特征并重构CSI）
% 全连接层：将融合特征扩展为卷积3输出尺寸
fcExpand = fullyConnectedLayer(flattenSize, 'Name', 'fc_expand');
reluExpand = reluLayer('Name', 'relu_expand');

% 重塑层：将向量恢复为卷积3输出的特征图形状
reshapeLayer = reshapeLayer(conv3OutputSize, 'Name', 'reshape');

% 反卷积层1：上采样特征
deconv1 = transposedConvolution2dLayer(filterSize(3), numFilters(2), ...
    'Stride', stride(3), 'Padding', 'same', 'Name', 'deconv1');
relu4 = reluLayer('Name', 'relu4');

% 反卷积层2：进一步上采样
deconv2 = transposedConvolution2dLayer(filterSize(2), numFilters(1), ...
    'Stride', stride(2), 'Padding', 'same', 'Name', 'deconv2');
relu5 = reluLayer('Name', 'relu5');

% 反卷积输出层：重构CSI（实值矩阵，维度=输入）
deconv3 = transposedConvolution2dLayer(filterSize(1), 1, ...
    'Stride', stride(1), 'Padding', 'same', 'Name', 'deconv3');
tanhLayer = tanhLayer('Name', 'tanh_output');  % 限制输出范围[-1,1]

% 解码器层序列（需先融合编码器输出与LSTM输出）
decoderLayers = [
    % 融合层：拼接当前时间步压缩向量与LSTM时间特征
    concatenationLayer(1, 2, 'Name', 'fusion')  % 沿特征维度拼接
    
    fcExpand
    reluExpand
    reshapeLayer
    deconv1
    relu4
    deconv2
    relu5
    deconv3
    tanhLayer
    regressionLayer('Name', 'output')  % 回归任务（重构误差）
];

% 2.5 构建完整模型（连接编码器、LSTM、解码器）
% 使用层图（layerGraph）实现复杂连接
lgraph = layerGraph(encoderLayers);

% 添加LSTM层（输入为编码器的压缩向量）
lgraph = addLayers(lgraph, lstmLayer);
lgraph = connectLayers(lgraph, 'fc_compress', 'lstm_time');

% 添加解码器层并连接
lgraph = addLayers(lgraph, decoderLayers);
% 融合层输入1：当前时间步压缩向量（编码器输出）
lgraph = connectLayers(lgraph, 'fc_compress', 'fusion/in1');
% 融合层输入2：LSTM输出的时间特征
lgraph = connectLayers(lgraph, 'lstm_time', 'fusion/in2');

% 显示模型结构
figure;
plot(lgraph);
title('CsiNet-LSTM模型结构');


%% 3. 模型训练
% 3.1 训练参数设置
options = trainingOptions('adam', ...
    'MaxEpochs', 50, ...                % 最大训练轮数
    'MiniBatchSize', 32, ...            % 批处理大小
    'InitialLearnRate', 1e-4, ...       % 初始学习率
    'LearnRateSchedule', 'piecewise', ...% 学习率调度
    'LearnRateDropFactor', 0.5, ...     % 学习率衰减因子
    'LearnRateDropPeriod', 10, ...      % 每10轮衰减一次
    'ValidationData', {X_val, Y_val}, ...% 验证集
    'ValidationFrequency', 50, ...      % 每50步验证一次
    'Plots', 'training-progress', ...   % 显示训练过程
    'Verbose', true, ...                % 显示训练日志
    'Shuffle', 'every-epoch', ...       % 每轮打乱数据
    'GPU', 'yes');                     % 使用GPU加速（若无GPU可改为'no'）

% 3.2 训练模型
[trainedModel, trainInfo] = trainNetwork(X_train, Y_train, lgraph, options);


%% 4. 模型评估
% 4.1 在测试集上预测
Y_pred = predict(trainedModel, X_test);

% 4.2 反归一化（恢复原始尺度）
Y_pred_denorm = Y_pred .* X_std + X_mean;  % 预测值反归一化
Y_test_denorm = Y_test .* X_std + X_mean;  % 真实值反归一化

% 4.3 计算重构误差：归一化均方误差(NMSE)
% 转换为复数CSI矩阵
nmse = zeros(1, numel(testIdx));
for s = 1:numel(testIdx)
    for t = 1:timeSteps
        % 真实CSI（复数）
        H_true = Y_test_denorm(1:Nr, :, t, s) + 1i*Y_test_denorm(Nr+1:end, :, t, s);
        % 预测CSI（复数）
        H_pred = Y_pred_denorm(1:Nr, :, t, s) + 1i*Y_pred_denorm(Nr+1:end, :, t, s);
        % 计算NMSE（单位：dB）
        nmse(s) = 10*log10(norm(H_true - H_pred, 'fro')^2 / norm(H_true, 'fro')^2);
    end
end
meanNMSE = mean(nmse);
fprintf('测试集平均NMSE: %.2f dB\n', meanNMSE);

% 4.4 可视化部分结果（第1个测试样本的第5个时间步）
s_idx = 1;  % 样本索引
t_idx = 5;  % 时间步索引

% 真实CSI的幅度
H_true_abs = abs(Y_test_denorm(1:Nr, :, t_idx, s_idx) + 1i*Y_test_denorm(Nr+1:end, :, t_idx, s_idx));
% 预测CSI的幅度
H_pred_abs = abs(Y_pred_denorm(1:Nr, :, t_idx, s_idx) + 1i*Y_pred_denorm(Nr+1:end, :, t_idx, s_idx));

figure;
subplot(1,2,1);
imagesc(H_true_abs); colorbar; title('真实CSI幅度');
subplot(1,2,2);
imagesc(H_pred_abs); colorbar; title('重构CSI幅度');
suptitle(['样本' num2str(s_idx) ' 时间步' num2str(t_idx) ' (NMSE: ' sprintf('%.2f', nmse(s_idx)) ' dB)']);


%% 5. 模型保存
save('CsiNet_LSTM_Model.mat', 'trainedModel', 'X_mean', 'X_std', 'Nr', 'Nt');
fprintf('模型已保存至CsiNet_LSTM_Model.mat\n');

本文章已经生成可运行项目