▲32QAM调制+软解调通信链路matlab误码率仿真_qam的软解调matlab实现-优快云博客

本文链接：https://blog.youkuaiyun.com/ccsss22/article/details/145557802

1.32QAM调制原理

正交幅度调制（QAM）是一种将幅度调制和相位调制相结合的调制方式。它通过同时改变载波的幅度和相位来表示不同的数字信息。对于MQAM，M表示调制阶数，它决定了星座图上信号点的数量。32QAM中，M = 32，意味着有32种不同的幅度和相位组合来表示信息。

32QAM的星座图是在复平面上分布着 32 个信号点。常见的 32QAM 星座图采用矩形星座图结构，其信号点可以分为不同的层次，每个信号点对应一个特定的二进制比特组合。通常，32QAM 的每个符号携带5个比特的信息。

将输入的二进制比特流按照每5个比特一组进行分组，然后根据星座映射表将每组比特映射到对应的星座点。例如，一种常见的32QAM星座映射规则如下（部分示例）：

2. 32QAM软解调原理

硬解调是指在接收端直接根据接收信号与星座点的距离，判决出最接近的星座点，然后根据星座映射规则恢复出对应的二进制比特。而软解调则不仅给出每个比特的判决结果，还给出每个比特为 0 或 1 的概率信息，即软信息。软信息可以在后续的信道解码过程中提供更多的有用信息，从而提高系统的误码性能。

对数似然比（LLR）是软解调中常用的一种度量，用于表示每个比特为 1 的概率与为 0 的概率之比的对数。对于第i个比特，其 LLR 定义为：

3.MATLAB程序

,,49,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,
    %第5位的软信息
    sf1(ij) = min([ abs(Xin(1,ij)-sf0(1))^2, abs(Xin(1,ij)-sf0(3))^2, abs(Xin(1,ij)-sf0(5))^2, abs(Xin(1,ij)-sf0(7))^2 ...
                                abs(Xin(1,ij)-sf0(9))^2, abs(Xin(1,ij)-sf0(11))^2, abs(Xin(1,ij)-sf0(13))^2, abs(Xin(1,ij)-sf0(15))^2 ...
                                abs(Xin(1,ij)-sf0(17))^2, abs(Xin(1,ij)-sf0(19))^2, abs(Xin(1,ij)-sf0(21))^2, abs(Xin(1,ij)-sf0(23))^2 ...
                                abs(Xin(1,ij)-sf0(25))^2, abs(Xin(1,ij)-sf0(27))^2, abs(Xin(1,ij)-sf0(29))^2, abs(Xin(1,ij)-sf0(31))^2]);
                            
    sf2(ij) = min([ abs(Xin(1,ij)-sf0(2))^2, abs(Xin(1,ij)-sf0(4))^2, abs(Xin(1,ij)-sf0(6))^2, abs(Xin(1,ij)-sf0(8))^2 ...
                                abs(Xin(1,ij)-sf0(10))^2, abs(Xin(1,ij)-sf0(12))^2, abs(Xin(1,ij)-sf0(14))^2, abs(Xin(1,ij)-sf0(16))^2 ...
                                abs(Xin(1,ij)-sf0(18))^2, abs(Xin(1,ij)-sf0(20))^2, abs(Xin(1,ij)-sf0(22))^2, abs(Xin(1,ij)-sf0(24))^2 ...
                                abs(Xin(1,ij)-sf0(26))^2, abs(Xin(1,ij)-sf0(28))^2, abs(Xin(1,ij)-sf0(30))^2, abs(Xin(1,ij)-sf0(32))^2 ]);
                            
                            
    Y(ij*5)       = sf1(ij) - sf2(ij);

 
   
end
                
   
output = Y;

msgr       = ones(size(output));
idx2       = find(output<0);
msgr(idx2) = 0;







figure % 创建图形窗口
subplot(421) % 创建3行1列的子图，并定位到第一个
plot(Ydemod1,'b','linewidth',1) % 绘制ASK调制信号
title('32QAM I解调'); % 设置标题
grid on % 打开网格

subplot(422) % 创建3行1列的子图，并定位到第一个
plot(Ydemod2,'b','linewidth',1) % 绘制ASK调制信号
title('32QAM Q解调'); % 设置标题
grid on % 打开网格


subplot(423) % 创建3行1列的子图，并定位到第一个
plot(yfilter1_,'b','linewidth',1) % 绘制16QAM调制信号
title('滤波I'); % 设置标题
grid on % 打开网格

subplot(424) % 创建3行1列的子图，并定位到第一个
plot(yfilter2_,'b','linewidth',1) % 绘制16QAM调制信号
title('滤波Q'); % 设置标题
grid on % 打开网格




subplot(425) % 定位到第二个子图
stairs(yfilter1_2,'b','linewidth',1) % 绘制载波信号
title('判决I输出'); % 设置标题
grid on % 打开网格


subplot(426) % 定位到第二个子图
stairs(yfilter2_2,'b','linewidth',1) % 绘制载波信号
title('判决Q输出'); % 设置标题
grid on % 打开网格


subplot(4,2,[7,8]) % 定位到第二个子图
stairs(msgr,'b','linewidth',1) % 绘制载波信号
title('并串输出'); % 设置标题
grid on % 打开网格

4.仿真结果

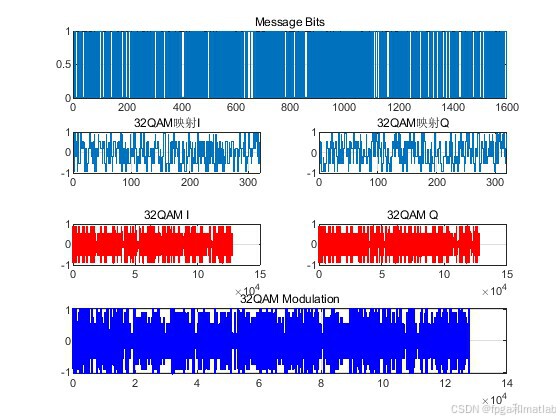
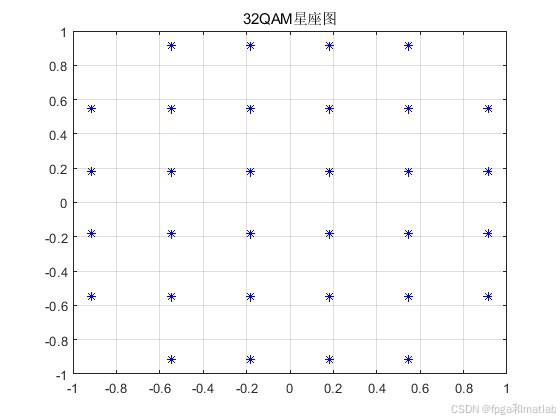
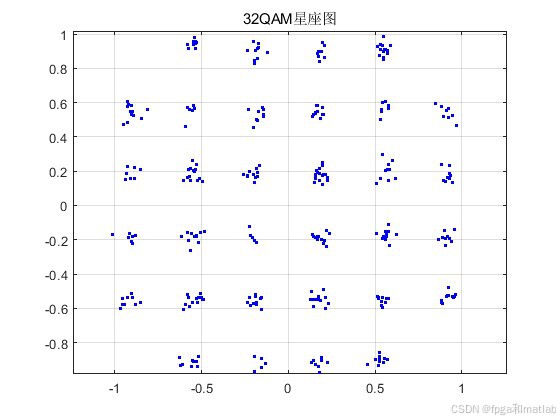
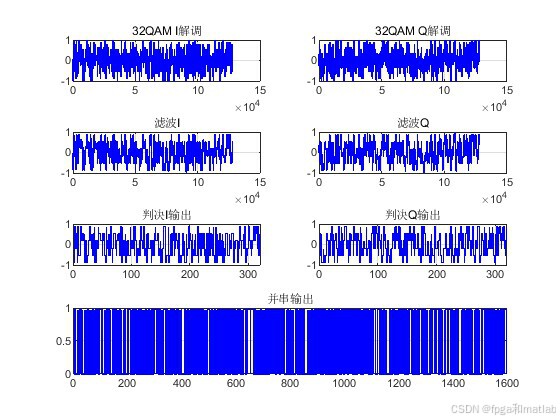
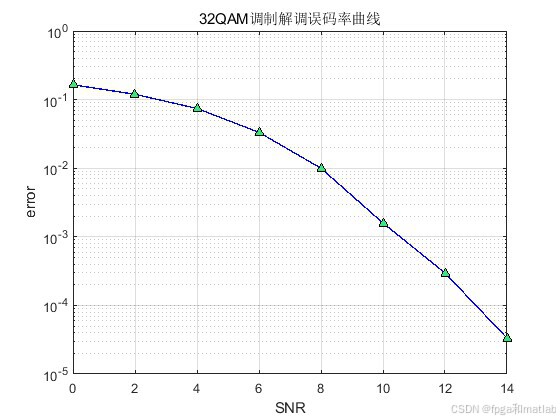
32QAM作为一种高阶调制方式，具有较高的频谱效率，但对信道质量要求也较高。软解调技术通过利用接收信号的软信息，可以有效提高系统的误码性能。通过Matlab仿真，验证了32QAM软解调通信链路在不同信噪比下的误码率性能。在实际通信系统中，需要根据具体的应用场景和信道条件，合理选择调制解调方式，以实现高效、可靠的数据传输。