基于遗传算法的多目标优化matlab仿真,输出最优帕累托值

目录

1. 遗传算法基础

2. 基于遗传算法的多目标优化

3.帕累托最优解集

4.MATLAB程序

5.仿真结果

---

1. 遗传算法基础

       遗传算法(Genetic Algorithm, GA)是一种模拟自然选择和遗传机制的搜索启发式算法，广泛应用于优化和搜索问题。它通过模拟生物进化过程中的自然选择、遗传和变异等机制，寻找问题的最优解或近似最优解。遗传算法流程：

1. 初始化种群：随机生成初始解的集合，即种群。
2. 适应度评估：根据问题的目标函数计算每个个体的适应度。
3. 选择操作：根据个体适应度选择个体进入下一代。
4. 交叉操作：随机选取两个个体进行交叉，产生新的后代。
5. 变异操作：以一定的概率改变后代中的某些基因。
6. 终止条件：当达到预设的停止条件时，算法结束；否则返回步骤2继续迭代。

        多目标优化问题是指同时优化两个或两个以上的冲突目标函数的问题。这类问题通常没有单一的最佳解，而是存在一组解，称为帕累托最优解集。

       给定两个解x 和y，如果对于所有的目标函数fi​，都有fi​(x)≤fi​(y) 并且至少存在一个i 使得 fi​(x)<fi(y)，那么称解x 支配解y。如果不存在任何其他解支配解 x，则称解x 是帕累托最优的。帕累托最优解集由所有帕累托最优解组成，表示为：

2. 基于遗传算法的多目标优化

       基于遗传算法的多目标优化通过引入特定的选择策略来解决多目标问题，从而找到帕累托最优解集。在多目标优化中，适应度分配需要考虑到每个个体在整个解空间中的相对位置。常用的适应度分配方法有：

• 非支配排序：将种群按照非支配关系分成不同的层次。
• 拥挤度距离：用来衡量同一层内个体之间的分散程度。

       多目标优化中的选择操作通常采用锦标赛选择或轮盘赌选择，但要结合非支配排序和拥挤度距离来确定选择个体的概率。

       交叉和变异操作与单目标遗传算法类似，但是需要确保产生的后代仍然处于可行域内。

3.帕累托最优解集

       帕累托最优解集是多目标优化问题的核心概念之一，它由一组相互之间非劣的解组成，反映了不同目标之间的权衡关系。通过使用遗传算法等方法，可以有效地找到帕累托最优解集，进而为决策者提供多样化的解决方案。

       帕累托最优解集是一个解集，其中不存在任何解在所有目标函数上都不劣于该解集中其他任何解，并且至少在一个目标函数上优于其他解。帕累托最优解集在目标空间中的投影被称为帕累托前沿。帕累托前沿是目标函数值的集合，表示为：

      给定两个解x 和y，如果对于所有的目标函数fi​，都有fi​(x)≤fi​(y) 并且至少存在一个i 使得fi​(x)<fi(y)，那么称解x 支配解y。如果不存在任何其他解支配解x，则称解x 是帕累托最优的。帕累托最优解集由所有帕累托最优解组成。

      帕累托最优解集的特性如下：

• 无序性：由于多目标优化问题中没有一个单一的最优解，帕累托最优解集通常包含多个解。
• 多样性：帕累托最优解集中的解反映了不同目标之间的权衡关系。
• 非劣性：帕累托最优解集中的解是相互之间非劣的，即不存在一个解在所有目标上都优于另一个解。

4.MATLAB程序

function [popbest,objectivebest]=Pareto(pop,objective,popbest,objectivebest)
% 过滤Pareto解
global popsize
c=1;
for i=1:popsize
%     for j=1:popsize
%         if objective(i,1)>objective(j,1)&objective(i,2)>=objective(j,2)|objective(i,1)>=objective(j,1)&objective(i,2)>objective(j,2)
%             j=j-1;
%             break;
%         end
%     end
%     if j==popsize
%         popbest(c,:)=pop(i,:);
%         objectivebest(c,:)=objective(i,:);
%         c=c+1;
%     end
    index1=find(objective(:,1)<objective(i,1));
    index2=find(objective(:,2)<=objective(i,2));
    index3=find(objective(:,1)<=objective(i,1));
    index4=find(objective(:,2)<objective(i,2));
    if isempty(intersect(index1,index2))&isempty(intersect(index3,index4))
        %不受支配
        group(c)=i;
        c=c+1;
    end
end
popbest=[popbest;pop(group,:)];
objectivebest=[objectivebest;objective(group,:)];
up4123

5.仿真结果

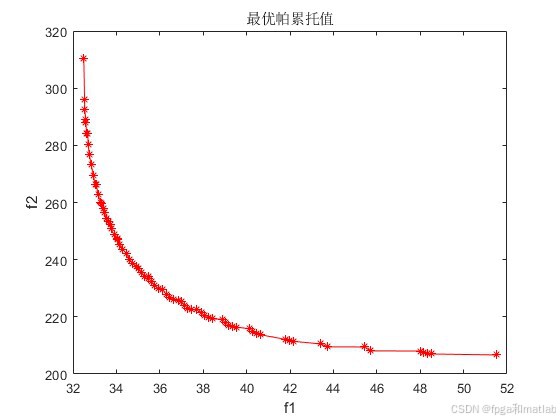
       基于遗传算法的多目标优化是一种强大的工具，能够处理复杂的多目标优化问题。通过使用非支配排序和拥挤度距离等技术，可以有效地找到帕累托最优解集。