【Kmeans】基于Kmeans的聚类算法的MATLAB仿真

0.完整源码获得方式

​​​​​​​方式1：微信或者QQ联系博主

方式2：订阅MATLAB/FPGA教程，免费获得教程案例以及任意2份完整源码

1.软件版本

MATLAB2021a

2.本算法理论知识

K-Means算法的思想很简单，对于给定的样本集，按照样本之间的距离大小，将样本集划分为K个簇。让簇内的点尽量紧密的连在一起，而让簇间的距离尽量的大。如果用数据表达式表示，假设簇划分为(C1,C2,...Ck)(C1,C2,...Ck)，则我们的目标是最小化平方误差E：

E=∑i=1k∑x∈Ci||x−μi||22E=∑i=1k∑x∈Ci||x−μi||22

其中μiμi是簇CiCi的均值向量，有时也称为质心，表达式为：

μi=1|Ci|∑x∈Cixμi=1|Ci|∑x∈Cix

3.核心代码

function [U1,U2]=count(u1,u2,x)

N1=0;%第一类个数
N2=0;%第二类个数
for i=1:210
d1(i)=dis1(u1,x,i);%x中所有点到u1的欧式距离
d2(i)=dis2(u2,x,i);%x中所有点到u2的欧式距离
if d1(i)>d2(i)
    N1=N1+1;
    W1(N1,:)=x(i,:);%划分到W1类中
   
else
    N2=N2+1;
    W2(N2,:)=x(i,:);%划分到W2类中
     
end
end
%重新计算聚类中心
%W1类
u=[0 0];
for i=1:N1
u=u+W1(i,:);
end
U1=(u/N1);

%W2类
u=[0 0];
for i=1:N2
u=u+W2(i,:);
end
U2=(u/N2);
%在图中画出
%[~,~,r1,r2,r3,r4]=data3();
%plot(r1,r2,'.',r3,r4,'+');
%hold on;
for i=1:N1 r1(i)=W1(i,1);end;
for i=1:N1 r2(i)=W1(i,2);end;
for i=1:N2 r3(i)=W2(i,1);end;
for i=1:N2 r4(i)=W2(i,2);end;
figure(2);
plot(r1,r2,'ro',r3,r4,'ms');
title('k均值聚类');

4.操作步骤与仿真结论

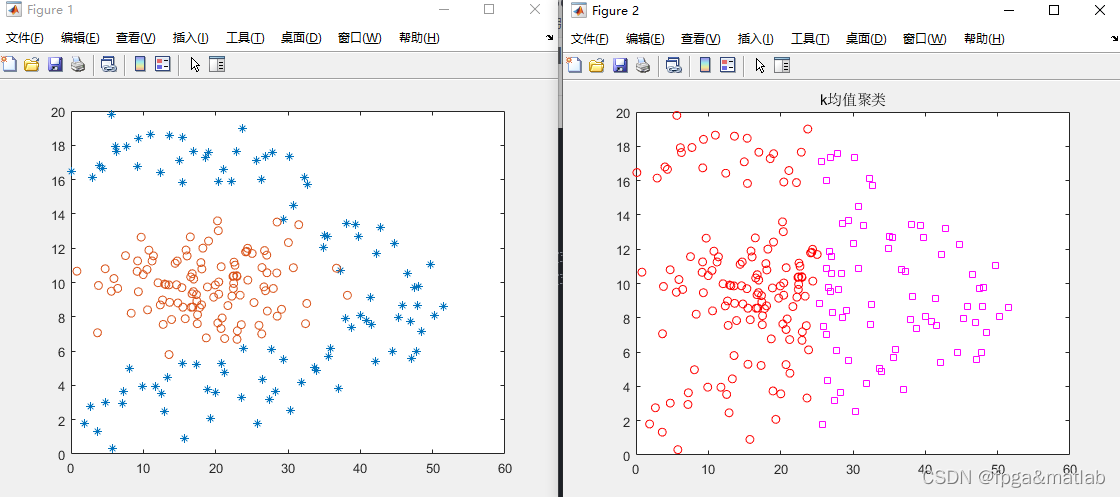
5.参考文献

[1]黄韬, 刘胜辉, 谭艳娜. 基于k-means聚类算法的研究[J]. 计算机技术与发展, 2011, 21(7):5.

出处-类目-编

D198